线性分类器理论基础、Fisher判别算法、Iris数据集实战

一、线性分类器理论基础

假设对一模式X已抽取n个特征，表示为：
$$X=（x_1,x_2,x_3,....x_n{）}^T$$
X是n维空间的一个向量
模式识别问题就是根据模式X的n个特征来判别模式属于ω1 ,ω2 , … , ωm类中的那一类。
例如这个图：三类的分类问题，它们的边界线就是一个判别函数

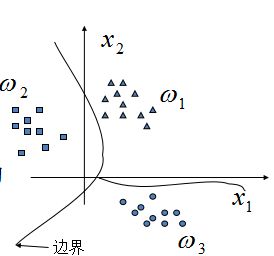
用判别函数进行模式分类，取决两个因素：
判别函数的几何性质：线性与非线性
判别函数的参数确定：判别函数形式+参数
判别函数包含两类：
一类是线性判别函数：
线性判别函数：线性判别函数是统计模式识别的基本方法之一，简单且容易实现。
广义线性判别函数：
所谓广义线性判别函数就是把非线性判别函数映射到另外一个空间（高维）变成线性判别函数
分段线性判别函数：
另一类是非线性判别函数
这里我们举一个多类问题的例子

先手工推导一下
首先确定判别边界

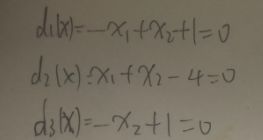
作图如下：有点丑，大概意思是对的

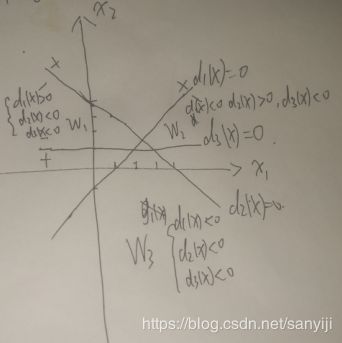
将X代入判别函数方程组并得到结果

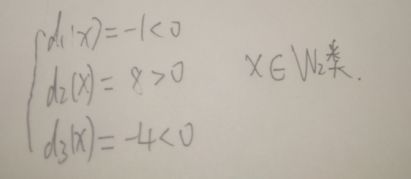
下面我们用python代码来实现一下
代码如下

def dragin(x1,x2):
    #三个判别式
    d1=-1*x1+x2+1
    d2=x1+x2-4
    d3=-1*x2+1
    if d1>0:
        print("属于第一类！")
    elif d2>0:
        print("属于第二类！")
    elif d3>0:
        print("属于第三类！")
while True:
    temp=input("输入要判定的一个模式的第一个参数:")
    one=int(temp)
    temp1=input("输入要判定的一个模式的第二个参数:")
    two=int(temp1)
    dragin(one,two)

结果如下：

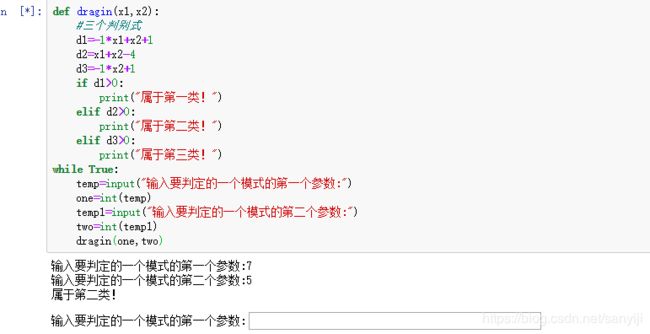
结果相同，证明我们算的还是没问题的。
理解了这些让我们开始进行更深层次的分类吧。

二、Fisher判别

1.算法描述

Fisher线性判别分析的基本思想：选择一个投影方向（线性变换，线性组合），将高维问题降低到一维问题来解决，同时变换后的一维数据满足每一类内部的样本尽可能聚集在一起，不同类的样本相隔尽可能地远。
Fisher线性判别分析，就是通过给定的训练数据，确定投影方向W和阈值w0， 即确定线性判别函数，然后根据这个线性判别函数，对测试数据进行测试，得到测试数据的类别。
线性判别函数的一般形式可表示成 $$g（X）=w^{T}X+w_0$$ 其中
$$X=\left\{\begin{array}{c}{X}_1\\ ...\\ X_d\end{array}\right\}\text{\hspace{1em}(1)}$$
$$W=\left\{\begin{array}{c}{W}_1\\ W_2\\ ...\\ W_d\end{array}\right\}\text{\hspace{1em}(2)}$$
Fisher选择投影方向W的原则，即使原样本向量在该方向上的投影能兼顾类间分布尽可能分开，类内样本投影尽可能密集的要求。

2.推导过程

Fisher判别分析是要实现有最大的类间距离，以及最小的类内距离

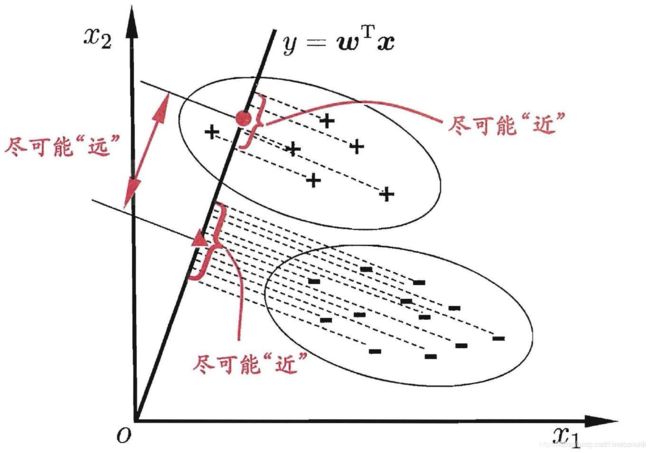
对于给定的数据集，D（已经设置好分类标签），Xi,Ui,∑i，分别表示给定类别ii 的集合，均值向量，协方差矩阵。现将数据投影到直线x=0上，则样本中心的投影为$$0=w_1\ast u_1+w_2\ast u_2+\cdots +w_n\ast u_n$$(n 为样本维度，接下来的讨论中将统一设置为2)，写成向量形式则为 $$w^{T}u=0$$如果将所有的样本都投影到直线上，则两类样本的协方差分别为$$w^T\sum 0w$$
$$w^T\sum 1w$$。要想达到较好的分类效果，应该是的同类样本的投影点尽可能的接近，也就是让同类样本投影点的协方差尽可能的小。即 $$w^T\sum 0w+w^T\sum 1w$$尽可能小。同时也应该保证不同类样本投影点尽可能的互相远离，即$$\Vert w^T{u}_0-w^T{u}_1\Vert$$ 尽可能大。如果同时考虑两者的关系可以得到下面需要最大化的目标：

$$J=\frac{\Vert w^T{u}_0-w^T{u}_1\Vert }{w^T{\sum }_{}^{}0w+w^T{\sum }_{}^{}1w}$$

3.python代码实现算法

IRIS数据集以鸢尾花的特征作为数据来源，数据集包含150个数据集，有4维，分为3 类，每类50个数据，每个数据包含4个属性，是在数据挖掘、数据分类中非常常用的测试集、训练集。
MATLAB代码如下：

clc
clear
data=xlsread('Iris.csv');
Iris1=data(1:50,1:4);
Iris2=data(51:100,1:4);
Iris3=data(101:150,1:4);
%类均值向量
m1 = mean(Iris1);
m2 = mean(Iris2);
m3 = mean(Iris3);
 
%各类内离散度矩阵
s1 = zeros(4);
s2 = zeros(4);
s3 = zeros(4);
for i=1:1:30
    s1 = s1 + (Iris1(i,:) - m1)'*(Iris1(i,:) - m1);
end
for i=1:1:30
    s2 = s2 + (Iris2(i,:) - m2)'*(Iris2(i,:) - m2);
end
for i=1:1:30
    s3 = s3 + (Iris3(i,:) - m3)'*(Iris3(i,:) - m3);
end
 
%总类内离散矩阵
sw12 = s1 + s2;
sw13 = s1 + s3;
sw23 = s2 + s3;
%投影方向
w12 = ((sw12^-1)*(m1 - m2)')';
w13 = ((sw13^-1)*(m1 - m3)')';
w23 = ((sw23^-1)*(m2 - m3)')';
%判别函数以及阈值T（即w0）
T12 = -0.5 * (m1 + m2)*inv(sw12)*(m1 - m2)';
T13 = -0.5 * (m1 + m3)*inv(sw13)*(m1 - m3)';
T23 = -0.5 * (m2 + m3)*inv(sw23)*(m2 - m3)';

%% 请补充输出判别函数



%% 请给下面代码添加必要注释 
kind1 = 0;
kind2 = 0;
kind3 = 0;
newiris1=[];
newiris2=[];
newiris3=[];
for i=31:50
    x = Iris1(i,:);
    g12 = w12 * x' + T12;
    g13 = w13 * x' + T13;
    g23 = w23 * x' + T23;
    if((g12 > 0)&(g13 > 0))
       newiris1=[newiris1;x];
        kind1=kind1+1;
    elseif((g12 < 0)&(g23 > 0))
         newiris2=[newiris2;x];
    elseif((g13 < 0)&(g23 < 0))
          newiris3=[newiris3;x];
    end
end    
for i=31:50
    x = Iris2(i,:);
    g12 = w12 * x' + T12;
    g13 = w13 * x' + T13;
    g23 = w23 * x' + T23;
    if((g12 > 0)&(g13 > 0))
      newiris1=[newiris1;x];
    elseif((g12 < 0)&(g23 > 0))
            kind2=kind2+1;
           newiris2=[newiris2;x];
    elseif((g13 < 0)&(g23 < 0))
            newiris3=[newiris3;x];
    end
end
for i=31:50
    x = Iris3(i,:);
    g12 = w12 * x' + T12;
    g13 = w13 * x' + T13;
    g23 = w23 * x' + T23;
    if((g12 > 0)&(g13 > 0))
       newiris1=[newiris1;x];
    elseif((g12 < 0)&(g23 > 0))
           newiris2=[newiris2;x];
    elseif((g13 < 0)&(g23 < 0))
            kind3=kind3+1;
            newiris3=[newiris3;x];
    end
end

correct=(kind1+kind2+kind3)/60;
fprintf('\n综合正确率：%.2f%%\n\n',correct* 100);

根据MATLAB代码修改为python代码
首先导入需要用的库

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt 
import seaborn as sns

然后导入数据集，数据集可以从这个网址下载下来，也可以直接使用这个链接进行导入
IRIS数据集

path=r'iris.data.txt'
df = pd.read_csv(path, header=0)

Iris1=df.values[0:50,0:4]
Iris2=df.values[50:100,0:4]
Iris3=df.values[100:150,0:4]

定义类均值向量

m1=np.mean(Iris1,axis=0)
m2=np.mean(Iris2,axis=0)
m3=np.mean(Iris3,axis=0)

定义类内离散度矩阵

s1=np.zeros((4,4))
s2=np.zeros((4,4))
s3=np.zeros((4,4))
for i in range(0,30,1):
    a=Iris1[i,:]-m1
    a=np.array([a])
    b=a.T
    s1=s1+np.dot(b,a)    
for i in range(0,30,1):
    c=Iris2[i,:]-m2
    c=np.array([c])
    d=c.T
    s2=s2+np.dot(d,c) 
    #s2=s2+np.dot((Iris2[i,:]-m2).T,(Iris2[i,:]-m2))
for i in range(0,30,1):
    a=Iris3[i,:]-m3
    a=np.array([a])
    b=a.T
    s3=s3+np.dot(b,a)

定义总类内离散矩阵

sw12 = s1 + s2;
sw13 = s1 + s3;
sw23 = s2 + s3;

定义投影方向

a=np.array([m1-m2])
sw12=np.array(sw12,dtype='float')
sw13=np.array(sw13,dtype='float')
sw23=np.array(sw23,dtype='float')

判别函数以及阈值T（即w0）

a=m1-m2
a=np.array([a])
a=a.T
b=m1-m3
b=np.array([b])
b=b.T
c=m2-m3
c=np.array([c])
c=c.T
w12=(np.dot(np.linalg.inv(sw12),a)).T
w13=(np.dot(np.linalg.inv(sw13),b)).T
w23=(np.dot(np.linalg.inv(sw23),c)).T
T12=-0.5*(np.dot(np.dot((m1+m2),np.linalg.inv(sw12)),a))
T13=-0.5*(np.dot(np.dot((m1+m3),np.linalg.inv(sw13)),b))
T23=-0.5*(np.dot(np.dot((m2+m3),np.linalg.inv(sw23)),c))

接着就可以计算正确率了

kind1=0
kind2=0
kind3=0
newiris1=[]
newiris2=[]
newiris3=[]
for i in range(30,49):
    x=Iris1[i,:]
    x=np.array([x])
    g12=np.dot(w12,x.T)+T12
    g13=np.dot(w13,x.T)+T13
    g23=np.dot(w23,x.T)+T23
    if g12>0 and g13>0:
        newiris1.extend(x)
        kind1=kind1+1
    elif g12<0 and g23>0:
        newiris2.extend(x)
    elif g13<0 and g23<0 :
        newiris3.extend(x)

for i in range(30,49):
    x=Iris2[i,:]
    x=np.array([x])
    g12=np.dot(w12,x.T)+T12
    g13=np.dot(w13,x.T)+T13
    g23=np.dot(w23,x.T)+T23
    if g12>0 and g13>0:
        newiris1.extend(x)
    elif g12<0 and g23>0:
       
        newiris2.extend(x)
        kind2=kind2+1
    elif g13<0 and g23<0 :
        newiris3.extend(x)
for i in range(30,49):
    x=Iris3[i,:]
    x=np.array([x])
    g12=np.dot(w12,x.T)+T12
    g13=np.dot(w13,x.T)+T13
    g23=np.dot(w23,x.T)+T23
    if g12>0 and g13>0:
        newiris1.extend(x)
    elif g12<0 and g23>0:     
        newiris2.extend(x)
    elif g13<0 and g23<0 :
        newiris3.extend(x)
        kind3=kind3+1
correct=(kind1+kind2+kind3)/60

print('判断出来的综合正确率：',correct*100,'%')

结果如下：

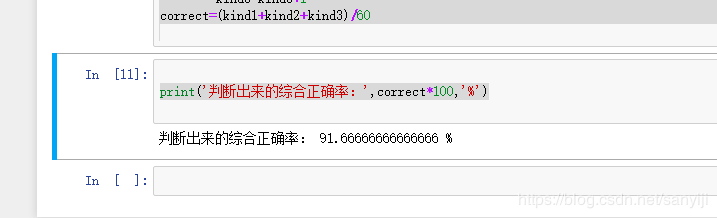
其他采用贝叶斯、BP神经网络、K-means等算法做的鸢尾花数据集（Iris）线性分类的文章，结果各有不同。采用Fisher判别，虽然判别过程比较复杂，理解其算法原理也有点难度，但是只要理解了其中的原理，其他的算法相信不在话下。

4.类间散度矩阵和类内散度矩阵

4.1.类内散度矩阵

设有M个类别，$${\Omega }_1,...{\Omega }_M$$,
Ω1类样本集 $$W=\left\{\begin{array}{c}{X}_1^{(i)},X_2^{(i)},...X_3^{(i)}\end{array}\right\}\text{\hspace{1em}(3)}$$
Ωi类的散度矩阵定义为:
$$S_w^{(i)}=1/N\sum _{k=1}^{N_i}(X_k^{(i)}-m_{}^{(i)}){({\mathbf{X}}_{\mathbf{k}}^{(\mathbf{i})}-{\mathbf{m}}_{}^{(\mathbf{i})})}^{\top }$$
其中，Sw(i)即是类Ωi的协方差矩阵。
总的类内散度矩阵为:
$$S_w=\sum _{i=1}^{M}P({\Omega }_i)S_w^{(i)}=\sum _{i=1}^{M}P({\Omega }_i)1/N\sum _{k=1}^{N_i}(X_k^{(i)}-m_{}^{(i)}){({\mathbf{X}}_{\mathbf{k}}^{(\mathbf{i})}-{\mathbf{m}}_{}^{(\mathbf{i})})}^{\top }$$
则: 迹[Sw}是所有类的特征方差的平均测度。

4.2.类间散度矩阵

第i个类别和第j个类别之间的散度矩阵定义为:$$S_B^{(ij)}=(m_{}^{(i)}-m_{}^{(j)}){({\mathbf{m}}_{}^{(\mathbf{i})}-{\mathbf{m}}_{}^{(\mathbf{j})})}^{\top }$$

总的类间散度矩阵可以定义为:$$S_B=1/2\sum _{i=1}^{M}P({\Omega }_i)\sum _{j=1}^{M}P({\Omega }_j)S_B^{(ij)}=1/2\sum _{i=1}^{M}P({\Omega }_i)\sum _{j=1}^{M}P({\Omega }_j)(m_{}^{(i)}-m_{}^{(j)}){({\mathbf{m}}_{}^{(\mathbf{i})}-{\mathbf{m}}_{}^{(\mathbf{j})})}^{\top }$$

令: m为总体均值，m=
$$\sum _{i=1}^{M}P({\Omega }_i)m_{}^{(i)}$$, 则有:
$$S_R=\sum _{i=1}^{M}P({\Omega }_i)(m_{}^{(i)}-m_{}^{}){({\mathbf{m}}_{}^{(\mathbf{i})}-{\mathbf{m}}_{}^{})}^{\top }$$

则: 迹{SB }是每一类的均值与全局均值之间平均距离的一种测度。

4.3.总体散度矩阵

总体散度矩阵可以定义为:
$$S_T=1/N\sum _{i=1}^N(X_{}^{(i)}-m_{}^{}){({\mathbf{X}}_{}^{(\mathbf{i})}-{\mathbf{m}}_{}^{})}^{\top }$$
其中N为总的样本数，$$N=\sum _{i=1}^M$$可以证明: $$S_T=S_w+S_B$$.
则: Sp 是全局均值向量的协方差矩阵，迹{ Sp )是特征值关于全局均值的方差和。
可以看出三个散度矩阵均为实对称矩阵。

三、Iris数据集实战

1.数据可视化

我们用到的工具是Seaborn，Seaborn是一个python的可视化库, 它基于matplotlib, 这使得它能与pandas紧密结合, 并且提供了高级绘图界面, 能更方便地完成探索性分析。如果没有下载这个库的首先找到Anaconda Prompt命令行，下载seaborn库 ，命令

pip install seaborn

1.1 relplot

首先还是读入数据集，注意上面网址下载的数据集是没有题头的，因为后面代码需要用，所以可以改一下数据集，如图所示添加这些就可以了

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
df_Iris = pd.read_csv(r'iris.data.txt')

然后绘制散点图

#sns初始化
sns.set()
#设置散点图x轴与y轴以及data参数
sns.relplot(x='SLC', y='SWC', data = df_Iris)
plt.title('SepalLengthCm and SepalWidthCm data analysize')

注意这两个位置

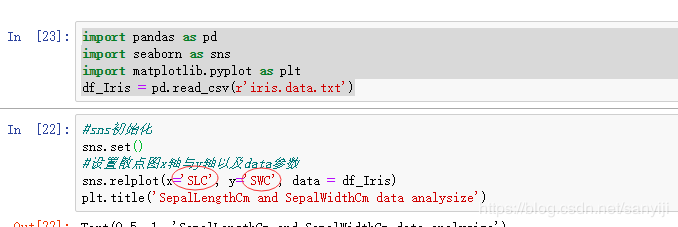
结果如下：

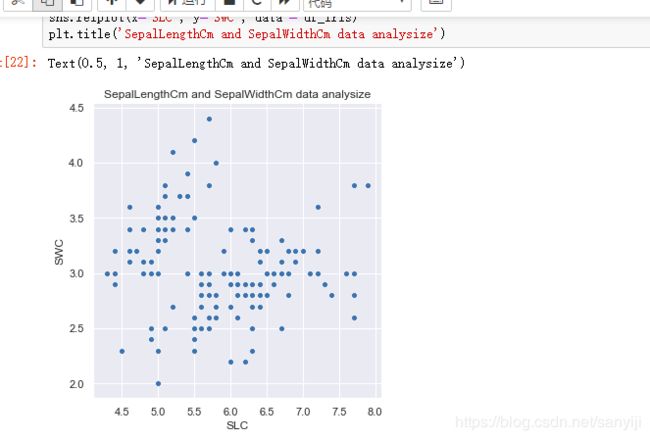
花萼的长度和宽度在散点图上分了两个簇, 而且两者各自都有一定的关系. 鸢尾花又分为三个品种, 不妨看看关于这三个品种的分布.
代码如下

#hue表示按照Species对数据进行分类, 而style表示每个类别的标签系列格式不一致.
sns.relplot(x='SLC', y='SWC', hue='SPE', style='SPE', data=df_Iris )
plt.title('SepalLengthCm and SepalWidthCm data by Species')

结果如图

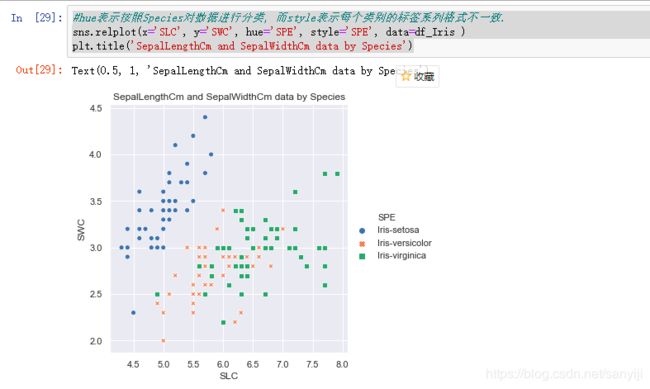
可以看到setosa这种花的花萼长度和宽度有明显的线性关系, 当然其他两种也存在一定的关系, 花萼的属性看完了, 看下花瓣的:
代码如下：

#花瓣长度与宽度分布散点图
sns.relplot(x='PLC', y='PWC', hue='Species', style='SPE', data=df_Iris )
plt.title('PetalLengthCm and PetalWidthCm data by Species')

结果如图：

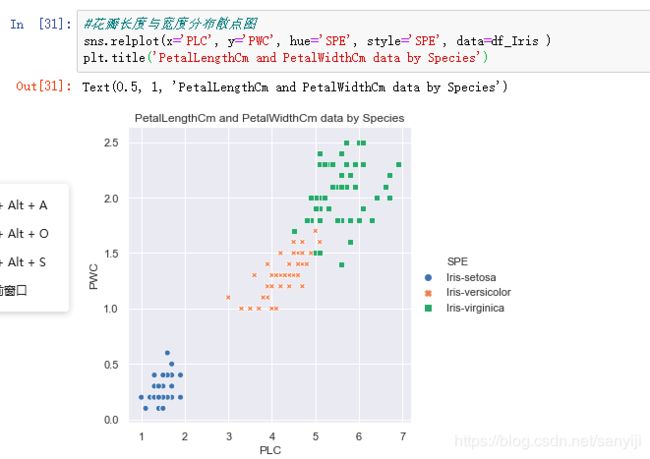
后面还有很多对比花瓣，花萼的长度宽度这些数据的可视化，可以参考下面这个博客进行学习。
添加链接描述

1.2 jointplot

绘制散点图和直方图
代码：

sns.jointplot(x='SLC', y='SWC', data=df_Iris)
sns.jointplot(x='PLC', y='PWC', data=df_Iris)

结果如图：


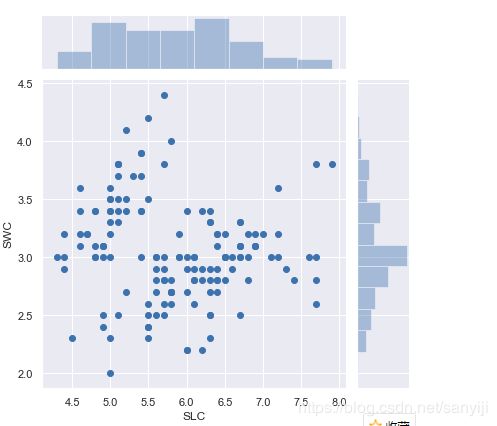
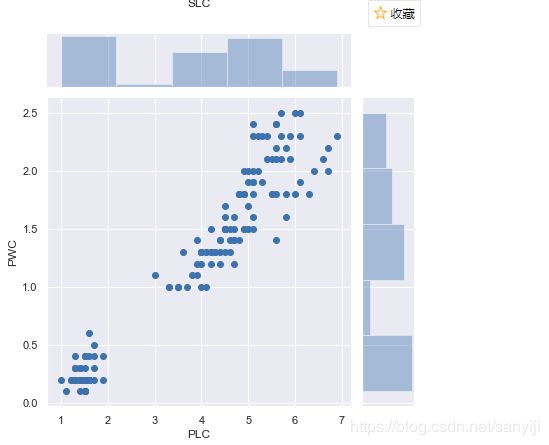
散点图和直方图同时显示, 可以直观地看出哪组频数最大, 哪组频数最小。对于频数的值, 在散点图上数点的话, 显然效率太低, 还易出错，所以我们可以使用distplot。

1.3 distplot

代码如下：
四个一起查看会有点分不清，所以选择一个个查看

sns.distplot(df_Iris.PWC, bins=5, hist=True, kde=False)
#sns.distplot(df_Iris.SLC,bins=8, hist=True, kde=False)
#sns.distplot(df_Iris.SWC,bins=13, hist=True, kde=False)
#sns.distplot(df_Iris.PLC, bins=5, hist=True, kde=False)

结果如图：

这种柱形图就很直观的表现出来数量，根本不需要自己去数。
下面介绍怎么以图样的形式展示四分位数。

1.4 boxplot

boxplot所绘制的就是箱线图, 它能显示出一组数据的最大值, 最小值, 四分位数以及异常点。不理解异常点的同样可以在刚刚那个博客得到解答。
直接上代码：
以SWC为例

sns.boxplot(x='SWC', data=df_Iris)

结果如图：

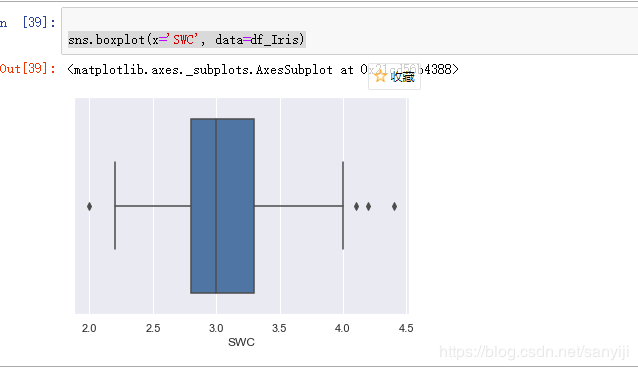
为了更直观地对比四个属性之间的关系, 可以将四个属性对应的数值合并在新的DataFrame Iris中。

代码如下：

import numpy as np
#对于每个属性的data创建一个新的DataFrame
Iris1 = pd.DataFrame({"Id": np.arange(1,151), 'Attribute': 'SLC', 'Data':df_Iris.SLC, 'Species':df_Iris.SPE})
Iris2 = pd.DataFrame({"Id": np.arange(151,301), 'Attribute': 'SWC', 'Data':df_Iris.SWC, 'Species':df_Iris.SPE})
Iris3 = pd.DataFrame({"Id": np.arange(301,451), 'Attribute': 'PLC', 'Data':df_Iris.PLC, 'Species':df_Iris.SPE})
Iris4 = pd.DataFrame({"Id": np.arange(451,601), 'Attribute': 'PWC', 'Data':df_Iris.PWC, 'Species':df_Iris.SPE})
#将四个DataFrame合并为一个.
Iris = pd.concat([Iris1, Iris2, Iris3, Iris4])
#绘制箱线图
sns.boxplot(x='Attribute', y='Data', data=Iris)

注意我之前给的网址下载的数据集里面没有ID这一项，如果要继续使用这个数据集。可以把txt转换为csv文件，然后用Excel打开，加入ID这一列。

然后保存为csv格式即可。
最后得到结果：

将鸢尾花的三种种类再加入到箱线图中:
代码如下;

sns.boxplot(x='Attribute', y='Data',hue='Species', data=Iris)

结果如图;

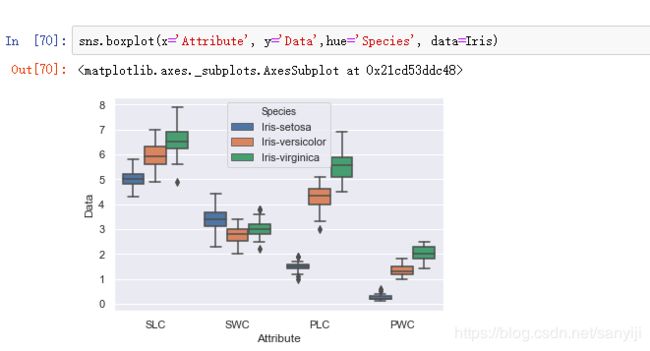
这样就很容易能够对比三个种类在四个属性中的表现状况。
下面再介绍一种更高级的四分位数展示方式: violinplot

1.5 violinplot

violinplot绘制的是琴图, 是箱线图与核密度图的结合体, 既可以展示四分位数, 又可以展示任意位置的密度。
代码如下；

sns.violinplot(x='Attribute', y='Data', hue='Species', data=Iris )

结果如图;

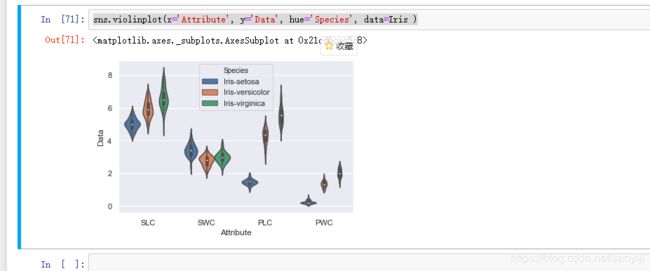
上图中具体细节显示不是很明显, 对于PWC都有些模糊了, 下面将拆分成四个小图, 另外为了和箱线图对比, 将箱线图也绘制出。
这里只展示花瓣宽度的结果
代码如下：

#花萼长度
# sns.boxplot(x='SPE', y='SLC', data=df_Iris)
# sns.violinplot(x='SPE', y='SLC', data=df_Iris)
# plt.title('SepalLengthCm data by Species')
#花萼宽度
# sns.boxplot(x='SPE', y='SWC', data=df_Iris)
# sns.violinplot(x='SPE', y='SWC', data=df_Iris)
# plt.title('SepalWidthCm data by Species')
#花瓣长度
# sns.boxplot(x='SPE', y='PLC', data=df_Iris)
# sns.violinplot(x='SPE', y='PLC', data=df_Iris)
# plt.title('PetalLengthCm data by Species')
#花瓣宽度
sns.boxplot(x='SPE', y='PWC', data=df_Iris)
sns.violinplot(x='SPE', y='PWC', data=df_Iris)
plt.title('PetalWidthCm data by Species')

结果如下：

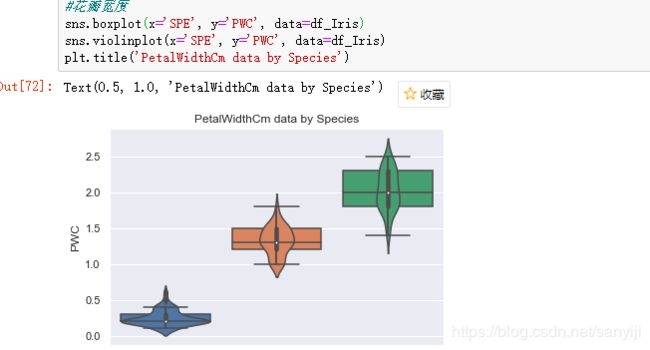
可以明显看出, 琴图中的白点就是中位数, 黑色矩形的上短边则是上四分位数Q3, 黑色下短边则是下四分位数Q1; 而贯穿矩形的黑线的上端点则代表最小非异常值, 下端点则代表最大非异常值; 黑色矩形外部形状则表示核概率密度估计。

1.6 pairplot

最后介绍一种图形, 它能直接显示各个特征之间的不同关系。
代码如下：

#删除Id特征, 绘制分布图
sns.pairplot(df_Iris.drop('ID', axis=1), hue='SPE')
#保存图片, 由于在jupyter notebook中太大, 不能一次截图
plt.savefig('pairplot.png')
plt.show()

因为图片太大，所以可能要等一会。
结果如图：


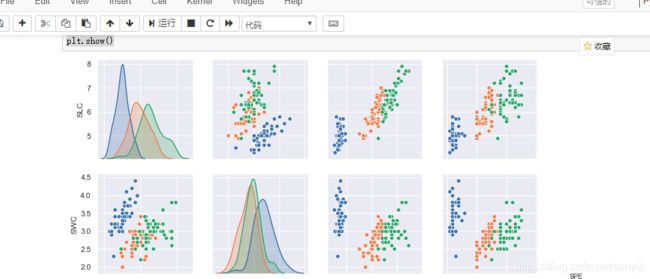
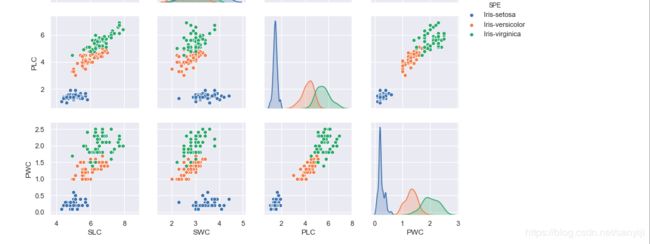
花萼的长度, 花萼的宽度, 花瓣的长度, 花瓣的宽度与花的种类之间均存在一定的相关性, 且对于这三个种类的分布,Iris-satosa在任何一种分布中较其他两者集中; 就同一种花的平均水平来看, 其花萼的长度最长, 花瓣的宽度最短; 就同一属性的平均水平来看, 三种花在除了花萼的宽度外的属性中平均水平均表现为:Iris- Virginica > Iris-versicolour > Iris-setosa.。

2.构建模型

这里我们使用决策树分类算法。
代码如下：

from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier

X = df_Iris[['SLC','SWC','PLC','PWC']]
y = df_Iris['SPE']
#将数据按照8:2的比例随机分为训练集, 测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
#初始化决策树模型
dt = DecisionTreeClassifier()
#训练模型
dt.fit(X_train, y_train)
#用测试集评估模型的好坏
dt.score(X_test, y_test)

结果如图：

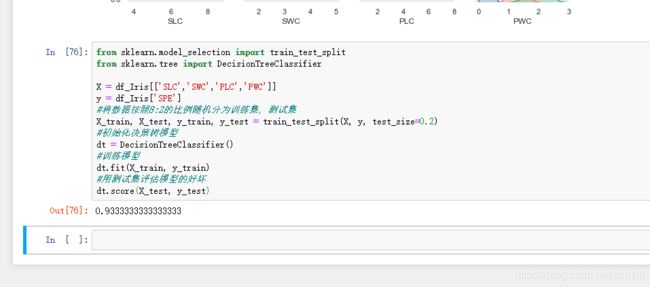
和上面用的Fisher判别算法相比准确率高了那么一点，但是就代码的复杂度来看，明显低于Fisher判别算法，只用了几行代码就成功的计算出了，但是明显太简单了也不便于新手理解其中的原理。所以两者各有各的优点吧。