树的遍历
def preorder(self, root):
if root:
self.traverse_path.append(root.val)
self.preorder(root.left)
self.preorder(root.right)
def inorder(self, root):
if root:
self.inorder(root.left)
self.traverse_path.append(root.val)
self.inorder(root.right)
def postorder(self, root):
if root:
self.postorder(root.left)
self.postorder(root.right)
self.traverse_path.append(root.val)递归
def recursion(level, param1, param2, ...):
# recrursion terminator
if level > MAX_LEVEL:
print_result
return
# process logic in current level
process_data(level, data ...)
# drill down
self.recursion(level + 1, p1, ...)
# reverse the current level status if needed
reverse_state(level)
分治法 Divide & Conquer
def divide_conquer(problem, param1, param2, ...):
# recursion terminator
if problem is None:
print_result
return
# prepare data
data = prepare_data(problem)
subproblems = split_problem(problem, data)
# conquer subproblems
subresult1 = self.divide_conquer(subproblems[0], p1, ...)
subresult2 = self.divide_conquer(subproblems[1], p1, ...)
subresult3 = self.divide_conquer(subproblems[2], p1, ...)
...
# process and generate the final result
result = process_result(subresult1, subresult2, subresult3, ...)
树的广度优先搜索 BFS
def bfs(graph, start, end):
queue = []
queue.append([start])
visited.add(start)
while queue:
node = queue.pop()
visited.add(node)
process(node)
nodes = generate_related_nodes(node)
queue.push(nodes)
# other processing work
...
树的深度优先搜索 DFS
# 递归写法
visited = set()
def dfs(node, visited):
visited.add(node)
# process current node here.
...
for next_node in node.children():
if not next_node in visited:
dfs(next_node, visited)
# 非递归写法
def dfs(self, tree):
if tree.root is None:
return []
visited, stack = [], [tree.root]
while stack:
node = stack.pop()
visited.add(node)
process(node)
nodes = generate_related_nodes(node)
stack.push(nodes)
# other processing work
...二分查询
left, right = 0, len(array) - 1
while left <= right:
mid = left + (right - left)/2
if array[mid] == target:
# find the target
break or return result
elif array[mid] < target:
left = mid + 1
else:
right = mid - 1
字典树
基本性质
- 根节点不包含字符,除根节点外每一个结点都只包含一个字符。
- 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个结点的所有子节点包含的字符都不相同。
static final int ALPHABET_SIZE = 256;
static class TrieNode {
TrieNode[] children = new TrieNode[ALPHABET_SIZE];
boolean isEndOfWord = false;
TrieNode() {
isEndOfWord = false;
for(int i = 0; i < ALPHABET_SIZE; i++)
children[i] = null;
}
}class TrieNode:
# Trie node class
def __init__(self):
self.children = [Node] * ALPHABET_SIZE
# isEndOfWord is True if node represent
# the end of the word
self.isEndOfWord = False
布隆过滤器
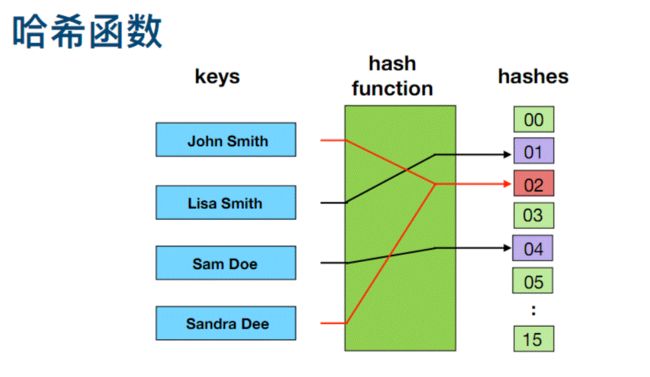 一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否存在于一个集合中。它的优点是空间效率和查询时间都远远超过一半的算法,缺点是有一定的误识别率和删除困难。
一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否存在于一个集合中。它的优点是空间效率和查询时间都远远超过一半的算法,缺点是有一定的误识别率和删除困难。