AtCoder Beginner Contest 042题解(ABCD)

AtCoder Beginner Contest 042题解(ABCD)

传送门

A - Iroha and Haiku (ABC Edition)

签到题，直接判断是否是两个$5$,一个$7$。

#include
using namespace std;
typedef long long ll;
const int N=1e5+5,M=1e6+5,inf=0x3f3f3f3f,mod=1e9+7;
#define mst(a) memset(a,0,sizeof a)
#define lx x<<1
#define rx x<<1|1
#define reg register
#define PII pair
#define fi first 
#define se second
int main(){
	int a[3];
	cin>>a[0]>>a[1]>>a[2];
	int cnt1=0,cnt2=0;
	for(int i=0;i<3;i++)
		if(a[i]==5) cnt1++;
		else if(a[i]==7) cnt2++;
	if(cnt1==2&&cnt2==1) puts("YES");
	else puts("NO"); 
	return 0;
}

B - Iroha Loves Strings (ABC Edition)

传送门

题意：给定$n$个长度为$L$的字符串，输出字典序最小的组合串。

思路：贪心，显然可以对$n$个字符串进行排序即可。

时间复杂度：$O(nlogn)$

#include
using namespace std;
typedef long long ll;
const int N=1e5+5,M=1e6+5,inf=0x3f3f3f3f,mod=1e9+7;
#define mst(a) memset(a,0,sizeof a)
#define lx x<<1
#define rx x<<1|1
#define reg register
#define PII pair
#define fi first 
#define se second
int main(){
	int n,l;
	cin>>n>>l;
	string a[n];
	for(int i=0;i<n;i++) cin>>a[i];
	sort(a,a+n);
	for(int i=0;i<n;i++)
		 cout<<a[i];
	return 0;
}

C - Iroha’s Obsession

传送门

思路：暴力枚举，因为数据范围很小，显然我们可以枚举答案，然后对每个数判断一下是否满足条件即可。

时间复杂度:$O(kn)$

#include
using namespace std;
typedef long long ll;
const int N=1e5+5,M=1e6+5,inf=0x3f3f3f3f,mod=1e9+7;
#define mst(a) memset(a,0,sizeof a)
#define lx x<<1
#define rx x<<1|1
#define reg register
#define PII pair
#define fi first 
#define se second
int vis[15],a[10];
int main(){
	int n,k;
	cin>>n>>k;
	for(int i=1,x;i<=k;i++)
		scanf("%d",&x),vis[x]=1;
	for(int i=n;;i++){
		int a[15]={};
		int x=i,cnt=0;
		while(x){
			a[++cnt]=x%10;
			x/=10;
		}
		int ok=1;
		for(int i=1;i<=cnt;i++)
			if(vis[a[i]]){
				ok=0;
				break;
			}
		if(ok) {
			cout<<i<<endl;
			break;
		}
	}
	return 0;
}

D - Iroha and a Grid

传送门

题意：给定$h\times w$的方格矩阵，左下角$a\times b$个格子不能走，每步只能往右或往下走，问从左上角走到右下角有多少种路径方式。

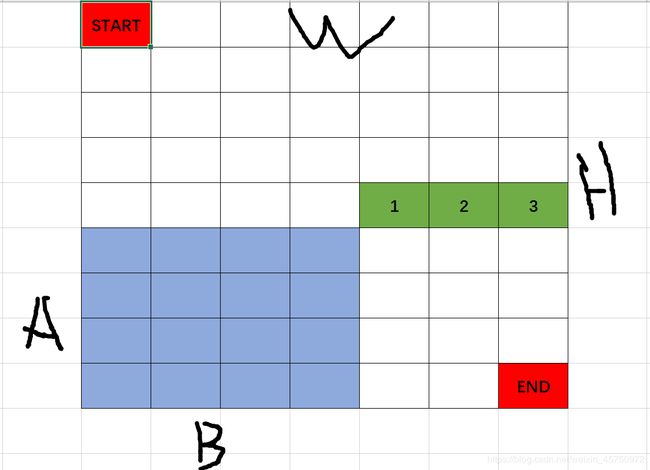
思路：组合数学，显然我们可以通过中间点$1,2,3$来计算答案，我们可以先分别计算出从起点走到$1.2,3$的方案数，
然后我们可以再计算出从$1,2,3$走到终点的方案数，最后根据乘法原理和费马小定理 再求和即可。
从$start$走到$1$的方式很好算，就是从$(H-A+1)+B$种路径中选出$B$中方式，即$C(H-A+1,B)$.
依次类推$C(H-A+2,B+1),C(H-A+3,B+2)\dots$
同理从$1,2,3$走到终点方式也可以计算。
$ep:1$走到终点，$C(W-B-1+A-1,W-B-1)$。
2走到终点：$C(W-B-2+A-1,W-B-2)$.
这里需要注意的是$1，2$都不能再往右走，不然会重复计算。
所以就等价于从它们的下面走到终点。

时间复杂度：$O(nlog(num))$

#include
using namespace std;
typedef long long ll;
const int N=2e5+10,M=1e6+5,inf=0x3f3f3f3f,mod=1e9+7;
#define mst(a) memset(a,0,sizeof a)
#define lx x<<1
#define rx x<<1|1
#define reg register
#define PII pair
#define fi first 
#define se second
ll fac[N];
ll ksm(ll a,ll n){
	ll ans=1;
	while(n){
		if(n&1) ans=ans*a%mod;
		a=a*a%mod;
		n>>=1; 
	}
	return ans;
}
ll C(ll n,ll m){
	return fac[n]*ksm(fac[m]*fac[n-m]%mod,mod-2)%mod;
}
int main(){
	int h,w,a,b;
	scanf("%d%d%d%d",&h,&w,&a,&b);
	fac[0]=1;
	for(int i=1;i<=2e5+5;i++)
		fac[i]=i*fac[i-1]%mod;
	ll ans=0;
	for(int i=b;i<=w-1;i++){
		ans+=C(h-a+i-1,i)*C(a+w-i-2,w-i-1)%mod;
		ans%=mod;
	}
	printf("%lld\n",(ans%mod+mod)%mod);
	return 0;
}