TEA加密算法与分组密码的ECB、CBC模式选定

TEA算法（Tiny Encryption Algorithm，小型加密算法）由剑桥大学计算机实验室的David Wheeler和Roger Needham于1994年发明。它是一种分组密码算法，其明文密文块为64比特，密钥长度为128比特。TEA算法利用不断增加的Delta(黄金分割率)值作为变化，使得每轮的加密是不同，该加密算法的迭代次数可以改变，建议的迭代次数为32轮。
TEA的结构类似于Feistel 密码结构，Feistel结构中一轮操作的左半部分与F函数输出是进行异或的运算（加解密流程相同）；而TEA加密是进行+操作，解密时进行-操作（加解密流程不同）。说TEA是小型加密算法，其实是说其F函数比较简单，不像DES的F函数那么复杂，TEA的F函数只是进行简单的移位、加法、异或等操作，但是这不意味着TEA加密算法不安全。

TEA的一轮结构如下所示（64bit明文分为等长左右两部分各32bit，128bit密钥分为等长4部分各32bit）：

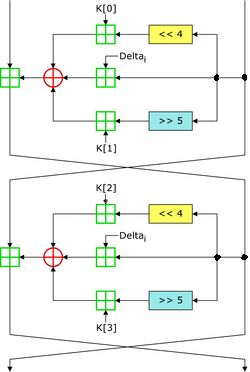
而XTEA是对TEA加密算法的改进，在F函数中加入了异或操作，其一轮结构如下所示：

对于XTEA我们也把它叫做TEA，只不过是改进版而已。TEA中Deltai - Deltai-1 = δ，而δ=（√5-1）* 2^31=（√5-1）2147483648，为什么要选择这个数呢？因为(√5-1)/2作为黄金分割点是一个人们不会怀疑的“后门”，当然你也可以用δ=（e-1） 2^31、δ=（π-1）* 2^31等来赋值Delta。

那么在编程中delta是一个无符号整数，delta = （√5-1）*2147483648 ≈2654435769.497230296477。取整为2654435769，即0X9E3779B9。

1、加密算法：

//XTEA加密,这里主要是为了分析分组密码模式的特点，关于TEA的加密解密代码实现可以自行百度
//8Byte(64bit)明文，16Byte(128bit)加密密钥
void encipher(unsigned int msg[2],unsigned int key[4])
{
    unsigned int i;
    unsigned int msg0=msg[0],msg1=msg[1],sum=0,delta=0x9E3779B9;//delta=(sqrt(5)-1)*2147483648
    for(i=0;i4) ^ (msg1>>5)) + msg1) ^ (sum + key[sum&3]);//sum&3（sum & 0000 0011）是取后2位，结果为0~3
        sum += delta;
        msg1 += (((msg0<<4) ^ (msg0>>5)) + msg0) ^ (sum + key[(sum >> 11)&3]);
    }
    //加密后的数据更新
    msg[0] = msg0;
    msg[1] = msg1;
}

2、解密算法：

//解密:加密的逆过程
//8Byte(64bit)密文，16Byte(128bit)解密密钥，属于私钥密钥，加密解密为同一个密钥
void decipher(unsigned int msg[2],unsigned int key[4])
{
    unsigned int i;
    unsigned int msg0 = msg[0],msg1 = msg[1],delta = 0x9E3779B9;
    unsigned int sum = delta * ROUNDS;//从加密的最终δ开始减
    for(i=0;i4) ^ (msg0>>5)) + msg0) ^ (sum + key[(sum >> 11)&3]);
        sum -= delta;
        msg0 -= (((msg1<<4) ^ (msg1>>5)) + msg1) ^ (sum + key[sum&3]);
    }
    //加密后的数据更新
    msg[0] = msg0;
    msg[1] = msg1;
}

3、我们对一个文件实现TEA加密：

#include 
#include 
#define ROUNDS 32

void encipher(unsigned int msg[2],unsigned int key[4]);
void decipher(unsigned int msg[2],unsigned int key[4]);

int main(int argc, char *argv[])
{
    if(argc != 5){
        printf("\nUsage:%s e(encipher) password sourceFileName outFileName",argv[0]);
        printf("\nUsage:%s e(decipher) password sourceFileName outFileName",argv[0]);
        return 0;
    }

    char passwd[100] = {0};//初始化为0，设为100Byte防止输入密码过长数组溢出
    strcpy(passwd,argv[2]);
    /*二进制文件是对内存的映射，文本文件是对屏幕的映射*/
    FILE * fpin = fopen(argv[3],"rb");//二进制形式打开
    FILE * fpout = fopen(argv[4],"wb");

    if(fpin && fpout){
        unsigned int msg[2];
        while(!feof(fpin)){
            msg[0] = msg[1] = 0;
            if(fread(msg,1,8,fpin) == 0){//读输入文件8字节，8*8=64bit
                break;
            }
            if(argv[1][0] == 'e'){//argv[1]="e\0"
                encipher(msg,(unsigned int *)passwd);//分组加密
            }else if(argv[1][0] == 'd'){
                decipher(msg,(unsigned int *)passwd);//分组解密
            }
            fwrite(msg,1,8,fpout);//写输出文件
        }
    }
    fclose(fpin);
    fclose(fpout);

    return 0;
}

观察加密解密结果是成功的（密钥匹配则解密成功，不匹配则依旧是密文）：

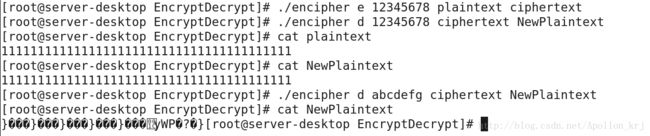
如果采用将明文分组（64bit一组）加密之后的结果（64bit）直接作为密文分组（64bit）的加密模式来加密。即所谓ECB（Eiectronic CodeBook，电子密码本模式）模式，我们上面的代码中使用的就是ECB模式。EBC的加密与解密流程如图所示：

（1）、加密（encryption）：

（2）、解密（decryption）：

如果要加密的信息存在多个组，且存在相同明文内容的不同组，其加密后的结果也是相同，即密文分组中可能存在重复出现的字符串。这样的加密方式是不安全。如下图所示（8个1为一组，密文中出现了重复的加密信息）：

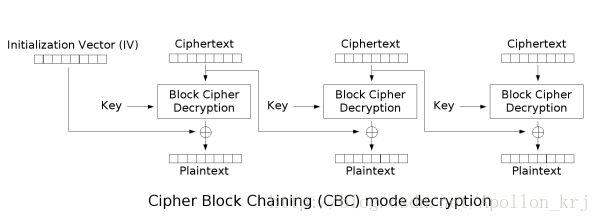
这是分组加密ECB模式的一个特点（流密码不存在该特点），每一个组之间不存在直接的关系，是相互独立的，那么ECB模式就不安全（如果要加密的信息只有一组就无所谓独立与否、安全与否）。那么如何使得有规律的明文加密后的密文也是无规律的？只要让后一个组的密文和前一个组的密文产生关联即可，如：CBC（Cipher Block Chaining mode，密文分组链接模式）,其加密与解密如下图所示：

（1）、加密：

（2）、解密：

我们看到CBC模式中，当前密文是根据前一组密文和当前明文异或后再经过key密钥加密形成的。而第一组由于不存在前一组加密结果，所以需要设定一个初始化向量（Initalization Vector，IV）。IV应该是随机产生的，这样即使明文和密钥都相同，由于IV不同加密的结果也不同，结果更加安全。当然除了CBC模式，分组加密还有CFB（Cipher FeedBack mode，密文反馈模式）、OFB（Output FeedBack mode，输出反馈模式）、CTR（CounTeR mode，计数器模式）。这几种模式比起ECB模式都要好很多，虽然ECB模式加解密都可以并行计算，简单快速，但是安全性差是其致命弱点。

4、CBC-TEA的简单实现：

//加密解密函数不变，只是在调用前/调用后进行了与向量iv的运算
int main(int argc, char * argv[])
{
    if(!((argc == 5 && argv[1][0] == 'e') || (argc == 7 && argv[1][0] == 'd'))){
        printf("Usage:%s e passwd inputFileName outputFileName\n",argv[0]);
        printf("Usage:%s d passwd inputFileName outputFileName iv_high_32bit iv_low_32bit\n",argv[0]);
        return 0;
    }

    unsigned int vi[2] = {0},tmp[2] = {0};
    if(argv[1][0] == 'e'){//加密的初始向量值随机产生，但rand()产生的随机值不太严谨，仅做测试用
        srand(time(NULL));
        vi[0] = rand();
        vi[1] = rand();

        printf("初始向量iv:%u(高32bit):%u(低32bit)\n",vi[1],vi[0]);
    }else if(argv[1][0] == 'd'){//解密的向量初始值和加密时相同
        vi[1] = atoi(argv[5]);
        vi[0] = atoi(argv[6]);
    }

    char passwd[100] = {0};
    strcpy(passwd, argv[2]);
    FILE * fpin = fopen(argv[3],"rb");
    FILE * fpout = fopen(argv[4],"wb");

    if(fpin && fpout){
        unsigned int msg[2],i=0;
        while(!feof(fpin)){
            msg[0] = msg[1] = 0;
            if(fread(msg,1,8,fpin) == 0){
                break;
            }
            if(argv[1][0] == 'e'){
                msg[0] ^= vi[0];    msg[1] ^= vi[1];//明文与向量异或
                encipher(msg,(unsigned int *)passwd);//加密
                vi[0] = msg[0];     vi[1] = msg[1];//产生的秘文做新的向量
            }else{
                tmp[0] = msg[0];    tmp[1] = msg[1];//保存秘文
                decipher(msg,(unsigned int *)passwd);//解密
                msg[0] ^= vi[0];    msg[1] ^= vi[1];//解密后与向量异或得明文
                vi[0] = tmp[0];     vi[1] = tmp[1];//用上次解密的秘文做下一次的向量
            }
            fwrite(msg,1,8,fpout);
        }
    }
    fclose(fpin);
    fclose(fpout);

    return 0;
}

测试结果：
我们先观察加密“1111111111111111111111111111111111111111”信息的密文是否有规律可寻，如下图（可以看到即使明文分组有规律，但是密文分组没有像ECB那样的规律）：

测试其他点（加密解密成功）：

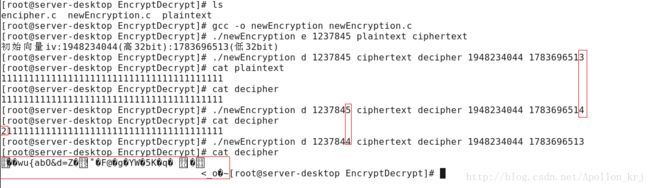
我们发现：在密钥错误的情况下是完全不能解密的。但是在密钥正确的情况下，即使初始向量错误，也能够解密部分信息。甚至我在测试时发现，即使初始向量错误，也可能完全解密，因为每一组解密后的明文正确与否依赖的是本组密文与上一组密文，只有第一组是依赖本组密文与初始向量的。即使初始向量错误，也只能影响第一组密文解密，而不会影响之后的组解密。这似乎是一个问题，但是我们要搞清楚，我们加入Initalization Vector的目的不是为了防止解密时如何如何，而是为了防止破解密码的人在密文中就发现规律。而Initalization Vector确实使得密文无规律可寻，那就达到了要求，只要密钥不被窃取到，即使知道了初始向量那也无关紧要（这就再次说明了密钥妥善保管的重要性）。