金融系统性风险的网络模型

Introduction

金融系统性风险的研究是一个跨学科的研究（其背景涉及economics and finance, statistical physics, ecology, engineering, applied mathematics, etc），因为金融市场可以看作是复杂系统，而对复杂系统的研究往往被视为跨学科的工作。
金融市场的参与者有：

• central banks
• commercial banks
• hedge funds
• insurance companies
• individual investors
  这些参与者通过买入或卖出金融资产交互而产生金融网络，其链接的类型主要有：

• financial liabilities
• cross-asset holdings
• correlations in asset returns

学术界对于金融系统性风险，目前还没有一个统一的定义，大致可以理解为：

Systemic risk is generally used in reference to an event that can trigger a huge collapse in a certain industry or overall economy.

如果从复杂系统的角度来对“系统性风险”进行理解的话，它来自于个体参与者对他们共同创造的市场总体动态做出反应。因此要了解系统性风险，必须考虑个体动态和集体动态之间的反馈回路（feedback loop）。

揭示systemic risk的关键在于：理解从微观到宏观的反馈（micro-to-macro feedback），即“涌现”（emergence）。
尽管在经济学文献中也有很多关于系统风险的研究，其方法通常基于博弈论game theory，金融和宏观经济模型finance and macroeconomic modeling，但在这里，我们关注的是在传统经济学之外开发的金融市场网络模型network models of financial markets。

把金融系统建模为一个复杂网络的优势是：

可以直接用来分析微观与宏观现象之间的复杂反馈，而无需过度简化金融连接的结构。网络的结构在将微观事件引导到集体现象中起着至关重要的作用。
此外，金融网络的实际经验结构很少采用程式化的拓扑形式，例如E-R随机图和星形图，但它需要更复杂的结构，例如multiplex，bipartite，core-periphery和time-varying networks，具体取决于相关金融链接的属性。 传统的经济模型无法处理这种复杂而现实的网络结构。

清算机制

在金融网络的系统性风险分析中，“清算”是核心的机制，因为不同交易的结算发生于这个相互承诺的网络中。
因此，它构成了导致可观察到的流动性问题，付款失败，损失和破产的结构基础。

Eisenberg–Noe algorithm

1. 基本原理：
   假设交易对手A和B之间的债务合同为：数额为$L_{ab}$在时间$T$由A支付给B。
   但是，在实际操作中B有可能不能够或者不愿意在时间T按时等额还钱给A。因此，必须考虑债务的等级，即偿还此债务相对于其他债务的优先级。此外，除了确定性合同的额度之外，交易对手B更对合同到期前A违约的概率（PD）及违约损失（LGD）感兴趣。
   所有银行需在到合同期时清算其付款，双边合同也同样如此。

市场中的不透明性和信息不对称性导致不同金融机构的信用风险估计与实际风险之间普遍存在差异。

2. 前提假设：
   从某种意义上说，“偿还债权人的资金数额是与借出的资金数额成比例地内生确定的”从经济上讲是明智的。 但是，在现实世界中，这种理想的配置可能不可行，尤其是在金融动荡中，因为评估破产银行的资产和债权人之间的谈判需要很长时间。
   模型中，金融系统为$F=(L,e)$一个非负负债矩阵和一个经营性现金流向量。
   The financial requirements for the Eisenberg–Noe clearing procedure are the following:
   (1) 所有元件的清算向量都小于或等于银行可用的现金流（Limited Liabilities）；
   (2) 银行应该尽可能多地还债，即银行的权益资本的优先级低于其同业间债务；
   (3) 还钱给各个债务人的金额应该根据其名义负债占总名义负债的比例来偿还。
3. 后续改进：
   考虑一个固定的外生恢复率（recovery rate），即债权人获得固定比例的付款；但是为了分析最坏情况，一般将其设为0（zero-recovery assumption）.
4. 相关研究
   Eisenberg和Noe（以下简称EN）的开创性论文引发了研究，并且自发表以来就提出了许多概括。 在这里，我们仅讨论那些引入最重要影响并概述其对系统性损失性质的影响的影响。
   Rogers and Veraart¹引入了违约代价（default cost）：
   一个无法偿付的金融机构可能：
   （1）需要快速地以一个较低的价格清算其有价值的外部资产，比如，由于抛售对价格的影响；
   （2）需要撤回其同业银行的资产，使对手方享有与到期前提早还款相关的折扣，即同业还款无需支付合同中那么多的本金加利息。
   因此，引入了两个因子$\alpha$和$\beta$来表征在清算时对外部资产和银行间同业资产的折扣。
   
   其动机是，尽管经济冲击造成的外部损失是由几乎无法控制的复杂经济动态驱动的，但监管机构可以通过实施特定政策来避免由于金融体系相互联系而可能造成的内生损失放大。
5. 模型的评述
   E-N模型和R-V模型都是完全决定性的（只要外部冲击足够大一定会发生违约传染的级联），他们分别构造了在金融系统中的资产重新分配和损失放大的机制。然而，这种机制仅由*实际破产*来触发（然而现实中风险的传染源头不一定非得等到某个银行破产），即，负债必须超过资产才能使银行传播其损失。因此，它们是违约传染机制（default contagion mechanism）。
6. 相应的解决方法
   (1) 首先，如DebtRank²中所述，直接说明当交易对手处于财务困境时激活的传播，并定义了危机蔓延机制；
   (2) 然后，统计在到期前外部资产价值的不确定性，即引入一种外部资产的概率分布。

由于双边银行敞口导致的违约级联

使用网络科学中的“社会传染”模型来描述此类传染现象

1. The Gai–Kapadia model
   Gai的模型是很大程度上基于Watts³的全球级联模型，该模型将在人与人之间的社会互动形成的网络上发生。

在Watts模型中，一个节点如何影响另一个节点的机制非常简单：当且仅当其至少一部分$R\in [0,1]$的邻居节点被激活时，节点才会被“激活”（或“感染”）。
因此，Watts的模型被归类为线性阈值模型或仅是阈值模型，其属于复杂传染类。 Watts模型的主要含义是，在随机连接的网络上，即使初始活动节点的很小一部分消失，只要网络不稀疏或过于密集，也可能导致很大一部分无限个节点被激活。
此临界现象称为全局级联，可以通过利用均值场近似来计算可能发生全局级联的解析条件，称为级联条件。

由于可以将人类的激活阈值重新解释为银行的违约阈值，因此理解社交网络文献中的阈值模型对于理解现有许多银行间网络的违约传染模型非常重要。
下面，将重点解释2种不同的计算级联规模的方法：

• 基于树的估计法（tree-based approximation）
• 生成函数法（generating function approach）

由于其简单性和可分析性，过去几年Gai-Kapadia模型经常被用作更复杂的金融传染模型的基准框架。下面来总结最简单的Gai-Kapadia模型中的一些重要假设：
（1）银行间贷款平均分布；
（2）银行间借贷形成了一个Erd}os–Re´nyi随机图；
（3）外部资产的风险没有考虑在内。
2. Extensions of the threshold cascade model
（1）异质的边权：
违约的条件不再是借款者违约的比例，而是所有银行间资产损失的比例：
$$\frac{{\sum }_{j\in N_i^{def}}{A}_{ij}^{IB}}{A_i^{IB}}>\overline{R}$$
有学者⁴考虑了一种情况从而可以得到平均级联规模的解析解：

网络的边权$w$是服从边$k$和$k^{\prime }$两侧节点度CDFs（累积分布函数）的随机变量；得出的结论是，权重异质性的增加将减小级联的大小。

（2）非ER网络：
ER随机图是在全球级联的解析模型中使用最广泛的网络结构；但是，没有实证的金融网络结构是ER随机的。
比如说，有研究证明了“银行间网络”的度分布服从“厚尾分布”，比如幂律分布、对数正态分布等。
此外，尽管大多数解析方法假设了一个局部树状结构，实证网络却呈局部簇状，并且边有一个叫做“同类/配性（assortativity：意味着，网络中的高度值节点，倾向于与高度值节点相连；低度值节点，倾向于与低度值节点相连。）”的度与度的关联。
即使在一个配置模型中，当假设为厚尾分布时其“聚类系数”也有可能很大。

In network science, the configuration model is a method for generating random networks from given degree sequence. It is widely used as a reference model for real-life social networks, because it allows the user to incorporate arbitrary degree distributions.

幸运的是，最近的研究开发了几种方法，其中局部循环的存在不会影响分析解析解的准确性。Radicci and Castellano ⁵ develop an alternative technique based on a message-passing algorithm, which gives an accurate approximation in networks with local clusters. Ikeda et al. ⁶ also show that the presence of local clusters will enhance the chance of global cascades.
另一个与ER随机图假设相背离的实证研究是：
在真实的金融网络中存在负的度与度相关性（disassoritivity，异配性），即度大的银行更倾向于与度小的银行产生贸易；
此外，当银行交易不同类型的资产时（比如，不同风险级别的贷款，长期、短期贷款，外汇敞口，衍生品等），银行间网络有可能呈现一个“多重网络”结构，

The essential difference between multiplex networks and multilayer networks is that in the latter, different layers can have different nodes while each layer has the same set of nodes in the former.
多重网络与多层网络的关键区别是，后者中不同层可以有不同的节点，但是前者每一层中的节点集都是一样的，不同层只是代表节点的不同属性。

Brummitt and Kobayashi⁷通过区分不同优先级的资产，将其放置在multiplex networks的不同层中，一般化了Gai-Kapadia的模型。他们考虑了一般情况即存在$M$级别的资产，表明级联条件通常由$M$个雅可比递归方程的迹给出。
（3）外部资产的风险：
Gai-Kapadia模型中仅考虑了银行间市场中由于还款失败而导致的级联；事实上，该渠道仅是系统性风险来源的一部分。
外部资产的贬值风险不仅是个别银行进行资产组合管理的主要部分，还是整个金融系统性风险的重要关注点；
近年来，对于重叠的投资组合下导致的风险渠道引发了大量的研究。这样一个同时对多个银行的冲击将加速传统的通过银行间敞口的传染过程。
在Gai-Kapadia模型中认为，外部资产的风险在引发传染时起作用。假设由不同银行持有的外部资产的收益是独立的，并且银行$i$持有的外部资产价格下降。如果外部资产价格的贬值使得银行的净资产下降至其违约条件，则它可能将导致银行$i$的债权人违约，引发一个传染过程。
然而，现实中外部资产由于相互关联，并且资产的波动使得银行与银行间资产负债表的健康程度区分开来。为了考虑到这些更现实的情况，许多研究进行了模拟，以了解外部资产相关性对系统风险的影响。Kobayashi⁷提供了一种简单的方法来概括响应函数（response function），以包括外部资产的值遵循概率分布的可能性，该可能性实际上对应于Watts模型，在该模型中，传染阈值是随机变量。

信用质量恶化造成的危机扩散

动机：交易对手违约传染对于实际目的的重要性在理论和经验上都受到了挑战。
Glasserman等人证明，在Eisenberg-Noe框架内，传染性对银行违约概率的贡献始终很小，Battiston等人指出，之所以如此，是因为“损失守恒”隐含地嵌入了Eisenberg-Noe算法中，从而阻止了它放大外来冲击。
从经验的角度来看，由于一小部分银行倒闭而导致的银行间网络系统发生“多米诺效应”的现象在现实中几乎很少发生。另一方面，在存在其他传染渠道的情况下，例如银行间的卖空交易和重叠的投资组合，表明银行间敞口网络可以极大地扩大遇险扩散。

卖空交易(Sell short or bear)：是买空交易的对称，亦称卖空。 证券市场上的证券投机者利用证券价格飞涨的时机，先借入大批的证券在市场上高价售出;待将来证券价格下跌以后，再低价买回证券，归还所借证券，进而从中获利的一种证券投机交易。 它具有以下特征：(1)卖出的股票和债券并非出售人所有，而是其从证券公司借入的。

除了与其他传染机制的相互作用之外，银行间风险敞口网络之所以重要的另一个原因如下：由于交易对手违约风险引起的传染模型假定损失仅在借款人违约后才从借款人传播到贷方。但是实际上，由于信用质量下降，即使在没有违约的情况下也可能发生损失。

经典模型：DebtRank
DebtRank是一个离散时间图（discrete-time map），它描述了系统遭受冲击后所有银行的权益演变。
在DebtRank中，动态银行可以处于两种状态：活跃 或 不活跃。
活跃银行是指在遭受损失时将困境转移给债权人的银行，而一旦将困境转移给债权人，银行就会变得不活跃。这并不一定意味着银行已违约，也不意味着银行不会遭受其他损失，而仅仅是意味着进一步的损失不会转移给其债权人。
银行间杠杆矩阵：代表$i$的权益损失百分比，对应于其$j$的敞口贬值1％。
$$W_{ij}/E_i(t)$$
实证应用：
Batision等人使用“DebtRank”模型对美国商业银行的研究表明，他们的算法可以有效地用于根据系统重要性对银行进行排名。通过证明相对较小的银行可能是系统上最重要的银行，并且由于DebtRank与网络中的集中度度量之间的类比，他们将有关某些银行可能“过于集中而无法倒闭”的思想引入了系统性风险的辩论中。

1. 压力测试的框架及步骤：
   （1）application of an exogenous shock to the system and estimation of direct losses;
   （2）propagation of distress through the DebtRank dynamic Eq and estimation of
   second-round losses;
   （3）further (third-round) losses caused by banks liquidating a common asset to target their initial leverage.
2. Extensions
   根据以上公式，由于节点在传播一次灾难后变为非活动状态，因此损失只能在网络中的一个循环中流动一次。
   为了说明损失进一步的传播，Bardoscia等人从资产负债表身份的迭代中得出以下经修改的动态过程：
   
   其中，$h_i(1)$表示影响银行$i$的初始外部冲击；
   此公式可以更容易理解系统在小扰动方面的稳定性。特别是，如果银行间杠杆率矩阵的最大特征值大于1，则冲击将被网络放大并导致系统中某些银行的违约。
   此外，DebtRank的基本假设是损失从借款人线性传播到贷方：借款人信用质量（权益资产）$x\%$的贬值，导致通过银行间资产使得其债权人也发生$x\%$的贬值，可以通过考虑表单的动态来放宽此假设：
   
   
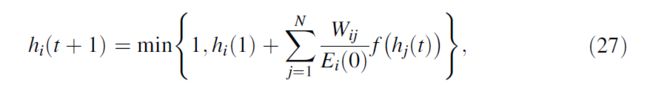
   此函数表示遇险传播规则的单参数系列，最早用于Gai-Kapadia外部资产贬值的阈值模型中。当$\alpha \to \infty$时恢复，而对于DebtRank中的线性规则则反映为$\alpha =0$.
   Bardoscia等人⁸还考虑了风险非线性传播的情况，并认为$f(x)$是递增的且凸的。
   他们分析了银行间杠杆矩阵的最大特征值，他们显示了网络空间中存在的轨迹，这些轨迹可以通过通常被认为可以增强金融市场稳定性的过程（即市场整合和多元化）将系统从稳定变为不稳定。
   然后，他们考虑了在系统中的银行之间随机添加链接的情况，但是这种方式使得每次添加链接时，都会保留每个银行的贷款总额。这意味着银行平均在增加其多样化。他们表明，通过这种多样化的过程，最初稳定的网络可能会变得不稳定。
   他们认为，在这种类型的动力学下，网络的不稳定性是由于银行间风险敞口网络中出现了特殊的周期性结构。

投资组合重叠和价格介导的传染

区别于“银行双边债务敞口”机制的传染：风险不止在债权人和债务人之间进行传染，事实上，损失也发生在持有共同资产的投资者身上，主要来自于资产价格的下跌。

上图为“投资组合重叠”的风险传染示意图，当银行1遇到困境需要清算其投资组合时，会导致其持有资产A的贬值，进一步导致持有相同资产A的银行2的资产缩水。
那么，可以被建模为“双向网络”的银行之间的“重叠投资组合模式”如何影响系统性风险？
由于持有共同资产且甩卖造成损失的影响最先被Cifuentes⁹ 所研究，他的模型是在Eisenberg-Noe模型的背景下。他考虑一个银行系统，该系统通过银行间借贷关系网络进行交互，并且所有银行都在其中投资一种共同的外部资产。银行受到资本约束（capital constraint），因此如果面临亏损，则需要清算对共同资产的部分投资。
此外，还有一部分研究也采用类似的方法，考虑一个或一类资产甩卖产生的影响。但是，他们的研究重点是根据银行同业拆借网络的性质对系统的稳定性进行研究。最近，重点转向研究重叠投资组合网络本身及其形状如何影响系统稳定性。
投资组合重叠网络往往使用一个“二分网络”来描述，如果我们考虑一个系统包含$N$个银行和$M$类资产，则可以用一个矩阵$Q$来描述，其中矩阵元素$Q_{ia}$表示——银行$i$持有资产$a$的股份数；此外，用$p_a$来表示资产$a$的价格。
除了网络之外，定义模型还需要两个主要要素：
（1）银行对其损失的反应：

其中，$A_i(t)$表示$t$时刻银行$i$的资产总量；
（2）资产对其清算的响应：

其中，$\{Q_{ia}(t)\}$表示集合：$\{Q_{1a}(t),Q_{2a}(t),...,Q_{Na}(t)\}$。
在关于重叠投资组合的网络模型的文献中，关于银行响应有两种常见的选择：
（1）要么银行一直处于被动状态，直到它们违约，这时他们清算其整个投资组合；
（2）要么它们的目标是一定水平的杠杆率，杠杆率的定义是资产的市值与资产之间的比率。

1. Threshold dynamics
   Huang等人¹⁰考虑银行在其违约之前一直处于被动状态，并在违约时清算其全部投资组合的情况，因此，银行对其损失的反应为：
   
   在其模型中，将资产价格假定为对清算的响应，
   
   其中，$\alpha >=0$是与资产$a$相关的市场影响参数。
   上述表达式意味着：在$t$时刻的资产价格线性地取决于到那时为止已清算的股份份额（相对于系统中持有的股份总数）。
   Caccioli等人¹¹提出了一个相似的投资组合重叠模型，其中资产价格的变化是对数线性相关的：
   
   Caccioli等人研究了当银行和资产数量很大时，系统在极限状态下的稳定性。 特别是，他们确定了在什么情况下，诸如银行的初始破产或资产贬值之类的小的初始动荡会导致全球范围的破产。
   
   上图为以“银行网络中平均度分布”以及“杠杆”为函数的“稳定/不稳定”区域，即通过将网络系统的不稳定指标映射到这两个参数上来绘制出。
2. Leverage targeting
   如果银行蒙受损失，其杠杆将上升，因此，需要进行重新平衡以降低风险。
   他们考虑了银行在$t$时刻通过清算一小部分投资，来对损失做出反应以维持杠杆率恒定：
   
   上式中，${\lambda }_i$是银行$i$的目标杠杆率，而参数$\gamma \in [0,1]$决定了银行尝试达到目标杠杆的速度。$\Delta A_i(t)$是银行在时间$t$清算的资产总值。
   要知道售出给定资产$a$的股份数量，需要除以银行投资组合中不同资产的数量$k_i$（此处假设银行对每种资产均清算相同的比例），再除以当前资产$a$的价格。
   因此，银行对损失的响应函数为：
   

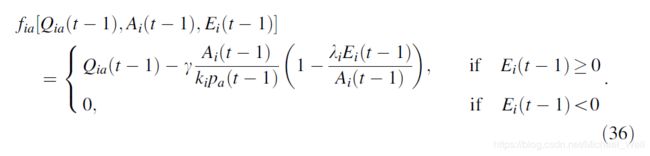
他们发现，银行通过先发制人的清算来降低个人风险的尝试最终大大拓宽了可以观察到全球级联的参数空间区域。(起了反作用)

Greenwood等人¹²提出了一个基于由于杠杆作用而引起冲击传播的压力测试的框架：在这种情况下，银行在$t$时刻估计其损失，然后减小其投资规模以在$t+1$时恢复其初始杠杆，这对应于等式（36）中给出的映射，其中$\gamma =1$。
去杠杆化导致价格贬值，从而导致银行的按市价计价的损失，这将进一步需要去杠杆化，依此类推。
他们试图弄清不同因素对甩卖（fire-sales）蔓延造成的损失的影响，表明如果银行联系更紧密、规模更大、更杠杆化并且更容易受到初始冲击，那么银行对总体去杠杆化的贡献就越高。这必须与直接脆弱性的概念形成对比，直接脆弱性是银行对资产的直接敞口。
Greenwood的模型是基于Duarte and Eisenbach¹³衡量银行的总体脆弱性和系统重要性的框架，由于杠杆率、系统规模和对非流动资产的投资集中度的增加，他们能够分散对总体脆弱性的贡献。
Cont and Schaanning¹⁴考虑了一种介于被动投资者和目标投资者之间的动态变化。在他们的模型中，他们考虑到一个事实，即银行的杠杆率与法规允许的最大杠杆率之间通常存在缓冲。这样做是为了使他们不会因为相对较小的损失而被迫平仓。

平仓指的是证券以及期货市场上，持有空头部位的投资人，借由买进等量的契约以离开市场；或是持有多头部位的投资人，借由卖出等量的契约以离开市场。即以等量但相反买卖方向，来冲销原有的契约。

然后他们将银行视为被动投资者，直到其亏损使银行打破其杠杆约束条件为止。发生这种情况时，银行会尽力达到其目标杠杆，但是该目标低于监管制度所允许的最大值（以便恢复较小的缓冲）。
他们还区分了可以被清算并受到市场影响的有价证券（marketable securities）和不可出售的不可流动资产，因此不能被清算。去杠杆化只涉及有价证券。
他们还引入了不同银行投资组合之间的重叠矩阵，其中每种资产均以其流动性加权​​，他们表明，尽管许多金融机构的投资组合之间有零重叠，但它们都是通过二阶重叠连接在一起的。这意味着不考虑第二轮损失的压力测试可能会大大低估系统风险。
尽管冲击系统或重叠投资组合网络的构建可能存在随机性，但上述动力学过程都是确定性的。
Corsi等人¹⁴考虑了一个随机的动态过程，一个包含$N$个银行的系统随机选择$M$类资产中的$m$个进行投资，然而，其中$m$被计算为，在VaR约束条件下的银行最大化其利润相对应的银行多元化经营的最优值，这等效于杠杆目标。
那么，资产的价值就是取决于银行交易的线性市场影响项的总和 加上 随机成分，而随机成分又是公因子和特质成分的总和。
至于我们在此讨论的其他模型，投资组合的相对组成（包含的资产类型）不会随时间而变化，但是每次银行都会更改其在投资组合上的投资量以维持其目标杠杆。
Corsi等人的研究结果表明，随着多元化程度的提高，系统将从资产收益的时间序列固定的稳定状态转变为以泡沫和破裂为特征的不稳定状态。

银行间网络的经验结构

---

1. Rogers, L. C., & Veraart, L. A. (2013). Failure and rescue in an interbank network. Management Science, 59(4), 882–898. ↩︎

2. Battiston, S., Puliga, M., Kaushik, R., Tasca, P., & Caldarelli, G. (2012). Debtrank: Too central to fail? Financial networks, the Fed and systemic risk. Scientific Reports, 2, 541. ↩︎

3. Watts, D. J. (2002). A simple model of global cascades on random networks. Proceedings of the National Academy of Sciences USA, 99(9), 5766–5771. ↩︎

4. Hurd, T. R., & Gleeson, J. P. (2013). On Watts’ cascade model with random link weights. Journal of Complex Networks, 1(1), 25–43. ↩︎

5. Radicchi, F., & Castellano, C. (2016). Beyond the locally treelike approximation for percolation on real networks. Physical Review E, 93(3), 030302. ↩︎

6. Ikeda, Y., Hasegawa, T., & Nemoto, K. (2010). Cascade dynamics on clustered network. Journal of Physics: Conference Series, 221(1), 012005. ↩︎

7. Kobayashi, T. (2013). Network versus portfolio structure in financial systems. European Physical Journal B, 86(10), 434. ↩︎ ↩︎

8. Bardoscia, M., Battiston, S., Caccioli, F., & Caldarelli, G. (2017). Pathways towards instability in financial networks. Nature Communications, 8, 14416. ↩︎

9. Cifuentes, R., Ferrucci, G., & Shin, H. S. (2005). Liquidity risk and contagion. Journal of the European Economic Association, 3(2–3), 556–566. ↩︎

10. Huang, X., Vodenska, I., Havlin, S., & Stanley, H. E. (2013). Cascading failures in bi-partite graphs: Model for systemic risk propagation. Scientific Reports, 3, 1219. ↩︎

11. Caccioli, F., Shrestha, M., Moore, C., & Farmer, J. D. (2014). Stability analysis of financial contagion due to overlapping portfolios. Journal of Banking & Finance, 46, 233–245. ↩︎

12. Greenwood, R., Landier, A., & Thesmar, D. (2015). Vulnerable banks. Journal of Financial Economics, 115(3), 471–485. ↩︎

13. Duarte, F., & Eisenbach, T. M. (2015). Fire-sale spillovers and systemic risk. Staff Report no. 645. New York: Federal Reserve Bank of New York. ↩︎

14. Corsi, F., Marmi, S., & Lillo, F. (2016). When micro prudence increases macro risk: The destabilizing effects of financial innovation, leverage, and diversification. Operations Research, 64(5), 1073–1088. ↩︎ ↩︎