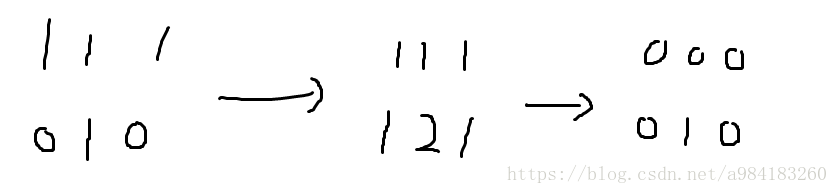POJ 3274 Gold Balanced Lineup
| Gold Balanced Lineup
Description Farmer John's N cows (1 ≤ N ≤ 100,000) share many similarities. In fact, FJ has been able to narrow down the list of features shared by his cows to a list of only K different features (1 ≤ K ≤ 30). For example, cows exhibiting feature #1 might have spots, cows exhibiting feature #2 might prefer C to Pascal, and so on. FJ has even devised a concise way to describe each cow in terms of its "feature ID", a single K-bit integer whose binary representation tells us the set of features exhibited by the cow. As an example, suppose a cow has feature ID = 13. Since 13 written in binary is 1101, this means our cow exhibits features 1, 3, and 4 (reading right to left), but not feature 2. More generally, we find a 1 in the 2^(i-1) place if a cow exhibits feature i. Always the sensitive fellow, FJ lined up cows 1..N in a long row and noticed that certain ranges of cows are somewhat "balanced" in terms of the features the exhibit. A contiguous range of cows i..j is balanced if each of the K possible features is exhibited by the same number of cows in the range. FJ is curious as to the size of the largest balanced range of cows. See if you can determine it. Input Line 1: Two space-separated integers, N and K. Output Line 1: A single integer giving the size of the largest contiguous balanced group of cows. Sample Input 7 3 7 6 7 2 1 4 2 Sample Output 4 Hint In the range from cow #3 to cow #6 (of size 4), each feature appears in exactly 2 cows in this range Source USACO 2007 March Gold |
官方解题报告——
Consider the partial sum sequence of each of the k features built by taking the
sum of all the values up to position i. The problem is equivalent to:
Given an array s[n][k], find i,j, with the biggest separation for which s[ i ]
[l]-s[j][l] is constant for all l.
The problem is now to do this efficiently. Notice that s[ i ][l]-s[j][l] being
constant for all l is equivalent to s[ i ][l]-s[j][l]=s[ i ][1]-s[j][1] for all
l, which can be rearranged to become s[ i ][l]-s[ i ][1]=s[j][l]-s[j][1] for all
l. Therefore, we can construct another array a[n][k] where a[ i ][j]=s[ i ][j]-
s[ i ][1] and the goal is to find i and j with the biggest separation for which
a[ i ][l]=a[j][l] for all l.
This can be done by sorting all the a[ i ] entries, which takes O(nklogn) time
(although in practice rarely will all k elements be compared). Another
alternative is to go by hashing, giving an O(nk) solution. Both solutions are
fairly straightforward once the final array is constructed.
意思就是对每天的增长进行累加 最后对累加的数组减去数组第一个特征的累加值
例子
2 3
7
2
转换到最后后 当i ,j 两行各位数都相同时 求max(i-j)即为答案
ac代码
#include
#include
#include
#include
#include