树状数组专题

树状数组专题

 

基础和原理就不多说了，做了一些树状数组的题，现在根据题目来大概分一下类。

1、一维 单点修改 区间查询

这是树状数组最基础的用法，query函数的判断条件如果习惯写成while(x)的请注意一下，如果x为负数的话，会造成死循环。要将数据偏移到1下标开始。

void add(int x,int k)
{
    while(x<=n)
    {
        sum[x]+=k;
        x+=lowbit(x);
    }
}
query(int x)
{
    int ans = 0;
    while(x>0)
    {
        ans+=sum[x];
        x-=lowbit(x);
    }
    return ans;
}

2、一维 区间修改 单点查询

操作是修改一个区间内的数，查询是只查询一个点。

如果区间范围很大，我们每次模拟修改一遍是非常耗时的。所以我们要优化每次对区间的操作，如果对区间[3,5]操作一次，x[3]++,x[6]--。

那么我们观察前六个数的前缀和为：0 0 1 1 1 0 ，前缀和的状态正好可以表示我们刚才的操作，而且去更新前缀和可以借助树状数组优化至logn。

因此一个位置的前缀和就可以表示这个位置的值。

修改：[x,y] + c

add(x,c) add(y+1,-c)

查询：query(x)

题目： hdu 1556

题解：http://blog.csdn.net/chy20142109/article/details/50674183

3、一维 区间修改 区间查询

如果对一个区间[x,y]都加上c

那么如果查询前i个数的和：s(i) 表示改变之前的和 s(i)'表示改变之后的和

(1) i>y s(i)’ = s(i) + ( y - x + 1 ) * c

(2) i∈[x,y] s(i)’ = s(i) + ( i - x + 1 ) * c

对于区间修改，我们可以参考第二种，在x位置加上c，y+1位置减去c，这样求得的前缀和的值就只在[x,y]内有效。观察(1)(2)都有一个固定的 (1-x)*c,所以我们可以在x位置先将其减去，再在y+1处加上y*c，用意为，如果范围超过y的话，这个前缀和正好就是( y - x + 1 ) * c。但是如果没超过怎么办？如果在范围内的话c还是有效的，所以加上i*c即可。

这样我们设计两个前缀和来维护。

第一个T1来维护增加量c

第二个T2来维护区间的实际增加量

所以每次操作[x,y]都加上一个值c就可以

T1:add(x,c)  add(y+1,-c)

T2:add( x , (1-x)*c )  add( y+1, y*c )

查询[1,x]

T2.query(x) + x * T1.query(x)

如果查询[x,y]，那么就先用查询y的结果减去查询x-1的结果即可。

题目： poj 3468

题解：http://blog.csdn.net/chy20142109/article/details/50674218

4、二维 单点修改 区间查询

有一个二维矩阵，每次修改一个点，或者查询一个矩形范围内的和。

void add(int x,int y,int k)
{
    while( x <= n )
    {
        int ty = y;
        while( ty <= n )
        {
            sum[x][ty]+=k;
            ty+=lowbit(ty);
        }
        x+=lowbit(x);
    }
}

int query(int x,int y)
{
    int ans = 0;
    while( x>0 )
    {
        int ty = y;
        while(ty>0)
        {
            ans+=sum[x][ty];
            ty-=lowbit(ty);
        }
        x-=lowbit(x);
    }
    return ans;
}

我看到有人用for来写，代码也很简洁。
void add(int x,int y,int k)
{
   for(int i = x; i <= n; i+=lowbit(i))
    for(int j = y; j <= n; j+=lowbit(j))
        sum[i][j]+=k;
}

int query(int x,int y)
{
    int ans = 0;
    for(int i = x; i > 0; i-=lowbit(i))
        for(int j = y; j > 0; j-=lowbit(j))
            ans+=sum[i][j];
    return ans;
}

二维树状数组也是维护一个前缀和，只不过一个增加了一维而已。

回到问题，如果是单点修改的话直接add(x,y,c)即可。

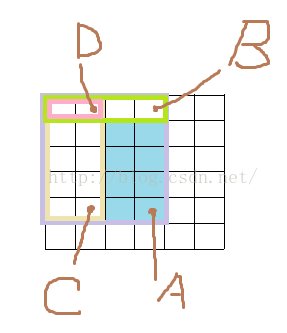
如果是区间查询的话，调用一次query(x,y)显然是求(1,1) 到 (x,y)范围内矩形的和。观察下图，我们没办法一次查询出来给定区间的值，但是我们可以通过计算得出。

现在如果要查询蓝色范围内的和

调用A点是求紫色边框

调用B点是求绿色边框

调用C点是求黄色边框

调用D点是求红色边框

那么A-B-C+D即是答案。

题目：poj 1195

题解：http://blog.csdn.net/chy20142109/article/details/50674194

5、二维 区间修改 单点查询

一次修改一个区间，或者查询一个点的值。

这个可以仿照一维情况下1->2的变化，因为要照顾区间修改，所以用一个点的前缀和来表示这个点的变化。我们确定起点和终点，在起点设置影响，那么将会从起点开始一直扩散到结束，所以我们在区间结束处做一次相反的操作来抵消区间终点之后造成的影响。

来看这个图，我们想对蓝色区间内修改一次，那么如果我们改变第一个蓝色的点会造成紫色区间内的修改，所以我们必须再通过修改来抵消这些多余的影响。

于是就有了黄色、绿色、红色的框...具体怎么写大家可以试着想一想。

题目：poj 2155

题解：http://blog.csdn.net/chy20142109/article/details/50674204

6、求逆序对

逆序对就是 i < j 并且 a[i] > a[j]，这样的存在算一对

我们可以将一个序列倒着考虑，如果处理到第i个数a[i]，先查询一下之前已经有多少个数比a[i]小，然后再将a[i]加进去。我们用树状数组来维护数的数量，就可以查询1~x范围内的数有多少个了。

题目： poj 2299 这道题是树状数组求逆序对模板，可以根据理解试着写一下

题目：poj 3067

题解：http://blog.csdn.net/chy20142109/article/details/50660162

还有一些问题也是借助树状数组统计来优化计算的。可以自己练习一下，树状数组用法比较活，代码也很少，是一个不错的数据结构。

1、  hdu 1541 

题解：http://blog.csdn.net/chy20142109/article/details/50660192

2、  poj 2481

题解：http://blog.csdn.net/chy20142109/article/details/50660168

3、  poj 2182

题解：http://blog.csdn.net/chy20142109/article/details/50660177

4、  poj 1990

题解：http://blog.csdn.net/chy20142109/article/details/50673968

5、poj 2309

题解：http://blog.csdn.net/chy20142109/article/details/50674157

6、poj 3321

题解：http://blog.csdn.net/chy20142109/article/details/50674049