十分钟带你了解Fisher线性判别
应用统计方法解决模式识别问题时,一再碰到的问题之一就是维度问题。在低维空间里计算上行得通的方法,在高维空间中往往行不通,如维度灾难等问题。因此,降低维数有时就会成为处理实际问题的关键。
简介
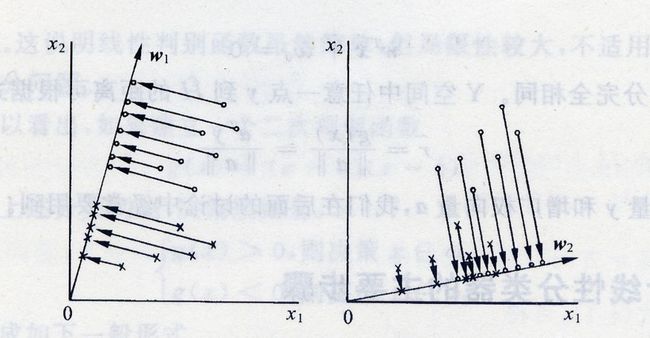
前面说到,在处理实际问题时,我们可能需要将维度降低以避免维度灾难等问题。我们不妨考虑把 d d d维空间的样本投影到一条直线上,形成一维空间,即把维数压缩到一维。当然,即使样本在 d d d维空间里形成若干紧凑的互相分得开的集群,当把它们投影到一条直线上时,也可能会是几类样本混在一起而变得无法识别。但是,在一般情况下,总可以找到某个方向,使在这个方向的直线上,样本的投影能分得开。那么,如何根据实际情况找到一条最好的、最易于分类的投影线呢?这就是Fisher判别方法所要解决的基本问题。如下图所示。
在讨论Fisher线性判别之前,我们不妨先看看样本是如何从 d d d维空间映射到一维空间的。
假设有一包含 N N N个 d d d维的样本集合 S S S,其中 N 1 N_1 N1个属于 w 1 w_1 w1的样本集合记为 S 1 S_1 S1, N 2 N_2 N2个属于 w 2 w_2 w2的样本集合记为 S 2 S_2 S2。若对 x i \mathbf{x}_i xi的分量做线性组合即可得到标量,
y i = w T x i , i = 1 , 2 , … , N y_i = \mathbf{w}^{T}\mathbf{x}_i, i = 1, 2, \dots, N yi=wTxi,i=1,2,…,N
这样,我们便可得到 N N N个一维样本 y i y_i yi组成的集合,并可分为两个子集 S 1 ′ S_1^{'} S1′和 S 2 ′ S_2^{'} S2′。
因此,我们只需找到一个矩阵 w ∈ R 1 × d \mathbf{w} \in \mathbb{R}^{1\times d} w∈R1×d即可将样本从 d d d维空间降到1维空间。此外, w \mathbf{w} w的值是无关紧要的,它仅是一个比例因子。重要的是选择 w \mathbf{w} w的方向。因为, w \mathbf{w} w的方向不同,将使样本投影后的可分离程度不同,从而直接影响的分类效果。因此,上述寻找最佳投影方向的问题,在数学上就是寻找最好的变换向量 w ∗ \mathbf{w}^{*} w∗的问题。
Fisher线性判别中的基本参量
在之前的内容,我们讨论了Fisher线性判别的基本概念。这里,在对Fisher线性判别进行详细地数学推导之前,我们先见到介绍一下涉及到的一些基本参量。
-
在 d d d维 X X X空间
-
各类样本的均值向量 m i \mathbf{m}_i mi
m i = 1 N i ∑ x ∈ S i x , i = 1 , 2 \mathbf{m}_i = \frac{1}{N_i}\sum_{\mathbf{x} \in S_i}\mathbf{x}, \quad i = 1, 2 mi=Ni1x∈Si∑x,i=1,2 -
样本类内离散度矩阵 S i S_i Si和总样本类内离散度矩阵 S w S_w Sw。其中 S w S_w Sw是对称半正定矩阵,而且当 N > d N>d N>d时通常是非奇异的。
S i = ∑ x ∈ S i ( x − m i ) ( x − m i ) T , i = 1 , 2 S w = S 1 + S 2 \begin{aligned} S_i &= \sum_{\mathbf{x} \in S_i}(\mathbf{x} - \mathbf{m}_i)(\mathbf{x} - \mathbf{m}_i)^{T}, \quad i = 1, 2 \\ S_w &= S_1 + S_2 \\ \end{aligned} SiSw=x∈Si∑(x−mi)(x−mi)T,i=1,2=S1+S2 -
样本类间离散度矩阵 S b S_b Sb。其中, S b S_b Sb是对称半正定矩阵。
S b = ( m 1 − m 2 ) ( m 1 − m 2 ) T S_b = (\mathbf{m}_1 - \mathbf{m}_2)(\mathbf{m}_1 - \mathbf{m}_2)^{T} Sb=(m1−m2)(m1−m2)T
-
-
在1维 Y Y Y空间
- 各类样本均值 m ~ i \tilde{m}_i m~i
m ~ i = 1 N i ∑ y ∈ S i ′ y , i = 1 , 2 \tilde{m}_i = \frac{1}{N_i}\sum_{y \in S_i^{'}}y,\quad i = 1, 2 m~i=Ni1y∈Si′∑y,i=1,2 - 样本类内离散度 S ~ i 2 \tilde{S}_i^{2} S~i2和总样本类内离散度 S ~ w \tilde{S}_w S~w
S ~ i 2 = ∑ y ∈ S i ′ ( y − m ~ i ) 2 , i = 1 , 2 S ~ w = S ~ 1 2 + S ~ 2 2 \begin{aligned} \tilde{S}_i^{2} &= \sum_{y \in S_i^{'}}(y - \tilde{m}_i)^{2}, \quad i = 1, 2 \\ \tilde{S}_w &= \tilde{S}_1^{2} + \tilde{S}_2^{2} \\ \end{aligned} S~i2S~w=y∈Si′∑(y−m~i)2,i=1,2=S~12+S~22
- 各类样本均值 m ~ i \tilde{m}_i m~i
Fisher准则函数
ok!Fisher线性判别的基本参量已经介绍完毕,接下来就开始进入正题吧。
直观上看,为了样本映射后能线性划分,我们想要同一类的样本彼此靠近,不同类的样本彼此分离。因此,我们不妨定义函数如下,
J F ( w ) = ( m ~ 1 − m ~ 2 ) 2 S ~ 1 2 + S ~ 2 2 J_F(\mathbf{w}) = \frac{(\tilde{m}_1 - \tilde{m}_2)^{2}}{\tilde{S}_1^{2} + \tilde{S}_2^{2}} JF(w)=S~12+S~22(m~1−m~2)2
其中, m ~ 1 − m ~ 2 \tilde{m}_1 - \tilde{m}_2 m~1−m~2是两类样本均值之差, S ~ i 2 \tilde{S}_i^{2} S~i2是样本类内离散度。显然,应该使 J F ( w ) J_F(\mathbf{w}) JF(w)的分子尽可能大而分母尽可能小,即应该尽可能寻找使 J F ( w ) J_F(\mathbf{w}) JF(w)大的 w \mathbf{w} w作为投影方向。但上式中不显式包含 w \mathbf{w} w。因此,我们首先需要将 J F ( w ) J_F(\mathbf{w}) JF(w)转换为 w \mathbf{w} w的显函数。
由各类样本的均值可推出,
m ~ i = 1 N i ∑ y ∈ S i ′ y = 1 N i ∑ x ∈ S i w T x = w T m i \tilde{m}_i = \frac{1}{N_i}\sum_{y \in S_i^{'}}y = \frac{1}{N_i}\sum_{\mathbf{x} \in S_i}\mathbf{w}^{T}\mathbf{x} = \mathbf{w}^{T}\mathbf{m}_i m~i=Ni1y∈Si′∑y=Ni1x∈Si∑wTx=wTmi
这样,Fisher准则函数 J F ( w ) J_F(\mathbf{w}) JF(w)的分子可写成,
( m ~ 1 − m ~ 2 ) 2 = ( w T m 1 − w T m 2 ) 2 = w T ( m 1 − m 2 ) ( m 1 − m 2 ) T w = w T S b w \begin{aligned} (\tilde{m}_1 - \tilde{m}_2)^{2} &= (\mathbf{w}^{T}\mathbf{m}_1 - \mathbf{w}^{T}\mathbf{m}_2)^{2} \\ &= \mathbf{w}^{T}(\mathbf{m}_1 - \mathbf{m}_2)(\mathbf{m}_1 - \mathbf{m}_2)^{T}\mathbf{w} \\ &= \mathbf{w}^{T}S_b\mathbf{w}\\ \end{aligned} (m~1−m~2)2=(wTm1−wTm2)2=wT(m1−m2)(m1−m2)Tw=wTSbw
现在再来考察 J F ( w ) J_F(\mathbf{w}) JF(w)的分母与 w \mathbf{w} w的关系,
S ~ i 2 = ∑ y ∈ S i ′ ( y − m ~ i ) 2 = ∑ x ∈ S i ( w T x − w T m i ) = w T [ ∑ x ∈ S i ( x − m i ) ( x − m i ) T ] w = w T S i w \begin{aligned} \tilde{S}_i^{2} &= \sum_{y \in S_i^{'}}(y - \tilde{m}_i)^{2} \\ &= \sum_{\mathbf{x} \in S_i}(\mathbf{w}^{T}\mathbf{x} - \mathbf{w}^{T}\mathbf{m}_i) \\ &= \mathbf{w}^{T}[\sum_{\mathbf{x} \in S_i}(\mathbf{x} - \mathbf{m}_i)(\mathbf{x} - \mathbf{m}_i)^{T}]\mathbf{w} \\ &= \mathbf{w}^{T}S_i\mathbf{w}\\ \end{aligned} S~i2=y∈Si′∑(y−m~i)2=x∈Si∑(wTx−wTmi)=wT[x∈Si∑(x−mi)(x−mi)T]w=wTSiw
因此,有 S ~ 1 2 + S ~ 2 2 = w T ( S 1 + S 2 ) w = w T S w w \tilde{S}_1^{2} + \tilde{S}_2^{2} = \mathbf{w}^{T}(S_1 + S_2)\mathbf{w} = \mathbf{w}^{T}S_w\mathbf{w} S~12+S~22=wT(S1+S2)w=wTSww
将各式代入准则函数 J F ( w ) J_F(\mathbf{w}) JF(w),得
J F ( w ) = w T S b w w T S w w J_F(\mathbf{w}) = \frac{\mathbf{w}^{T}S_b\mathbf{w}}{\mathbf{w}^{T}S_w\mathbf{w}} JF(w)=wTSwwwTSbw
其中, S b S_b Sb为样本类间离散度矩阵, S w S_w Sw为总样本类内离散度矩阵。
w ∗ \mathbf{w}^{*} w∗的求取
不难发现, w ∗ \mathbf{w}^{*} w∗的求取实际上是一个有条件约束的优化问题。因为,在求解 w ∗ \mathbf{w}^{*} w∗的过程中,要始终保持 w T S w w ≠ 0 \mathbf{w}^{T}S_w\mathbf{w} \ne 0 wTSww̸=0。因此,我们需要使用拉格朗日乘子法求解 w ∗ \mathbf{w}^{*} w∗。
令分母为非零常数,即,
w T S w w = c ≠ 0 \mathbf{w}^{T}S_w\mathbf{w} = c \ne 0 wTSww=c̸=0
定义拉格朗日函数为,
L ( w , λ ) = w T S b w − λ ( w T S w w − c ) L(\mathbf{w}, \lambda) = \mathbf{w}^{T}S_b\mathbf{w} - \lambda(\mathbf{w}^{T}S_w\mathbf{w} - c) L(w,λ)=wTSbw−λ(wTSww−c)
其中, λ \lambda λ是拉格朗日乘子。将上式对 w \mathbf{w} w求偏导,得
∂ L ( w , λ ) ∂ w = S b w − λ S w w \frac{\partial L(\mathbf{w}, \lambda)}{\partial \mathbf{w}} = S_b\mathbf{w} - \mathbf{\lambda}S_w\mathbf{w} ∂w∂L(w,λ)=Sbw−λSww
令偏导数为零,有,
S b w ∗ − λ S w w ∗ = 0 S_b\mathbf{w}^{*} - \lambda S_w\mathbf{w}^{*}= 0 Sbw∗−λSww∗=0
即,
S b w ∗ = λ S w w ∗ S_b\mathbf{w}^{*} = \lambda S_w\mathbf{w}^{*} Sbw∗=λSww∗
其中, w ∗ \mathbf{w}^{*} w∗就是 J F ( w ) J_F(\mathbf{w}) JF(w)的极值解。因为 S w S_w Sw非奇异,将上式两边左乘 S w − 1 S_w^{-1} Sw−1,可得
S w − 1 S b w ∗ = λ w ∗ S_w^{-1}S_b\mathbf{w}^{*} = \lambda \mathbf{w}^{*} Sw−1Sbw∗=λw∗
上式为求一般矩阵 S w − 1 S b S_w^{-1}S_b Sw−1Sb的特征值问题。利用 S b = ( m 1 − m 2 ) ( m 1 − m 2 ) T S_b = (\mathbf{m}_1 - \mathbf{m}_2)(\mathbf{m}_1 - \mathbf{m}_2)^{T} Sb=(m1−m2)(m1−m2)T的定义,将上式左边的 S b w ∗ S_b\mathbf{w}^{*} Sbw∗写成,
S b w ∗ = ( m 1 − m 2 ) ( m 1 − m 2 ) T w ∗ = ( m 1 − m 2 ) R S_b\mathbf{w}^{*} = (\mathbf{m}_1 - \mathbf{m}_2)(\mathbf{m}_1 - \mathbf{m}_2)^{T}\mathbf{w}^{*} = (\mathbf{m}_1 - \mathbf{m}_2)R Sbw∗=(m1−m2)(m1−m2)Tw∗=(m1−m2)R
其中, R = ( m 1 − m 2 ) T w ∗ R = (\mathbf{m}_1 - \mathbf{m}_2)^{T}\mathbf{w}^{*} R=(m1−m2)Tw∗是一标量,所以 S b w ∗ S_b\mathbf{w}^{*} Sbw∗总在向量 ( m 1 − m 2 ) (\mathbf{m}_1 - \mathbf{m}_2) (m1−m2)的方向上。因此, λ w ∗ \lambda \mathbf{w}^{*} λw∗可写成,
λ w ∗ = S w − 1 ( m 1 − m 2 ) R \lambda \mathbf{w}^{*} = S_w^{-1}(\mathbf{m}_1 - \mathbf{m}_2)R λw∗=Sw−1(m1−m2)R
因此,可有
w ∗ = R λ S w − 1 ( m 1 − m 2 ) \mathbf{w}^{*} = \frac{R}{\lambda}S_w^{-1}(\mathbf{m}_1 - \mathbf{m}_2) w∗=λRSw−1(m1−m2)
由于我们的目的是寻找最佳的投影方向, w ∗ \mathbf{w}^{*} w∗的比例因子对此并无影响,因此可忽略比例因子 R λ \frac{R}{\lambda} λR,有
w ∗ = S w − 1 ( m 1 − m 2 ) \mathbf{w}^{*} = S_w^{-1}(\mathbf{m}_1 - \mathbf{m}_2) w∗=Sw−1(m1−m2)
总结
- w ∗ \mathbf{w}^{*} w∗是使Fisher准则函数 J F ( w ) J_F(w) JF(w)取极大值时的解,也就是 d d d维 X X X空间到一维 Y Y Y空间的最佳投影方向。有了 w ∗ \mathbf{w}^{*} w∗,就可以把 d d d维样本x投影到一维,这实际上是多维空间到一维空间的一种映射,这个一维空间的方向 w ∗ \mathbf{w}^{*} w∗相对于Fisher准则函数 J F ( w ) J_F(w) JF(w)是最好的。
- 利用Fisher准则,就可以将 d d d维分类问题转化为一维分类问题,然后,只要确定一个阈值 T T T,将投影点 y i y_i yi与 T T T相比较,即可进行分类判别。
参考文献
黄庆明,《第三章.ppt》