使用BloomFilter布隆过滤器解决缓存穿透、垃圾邮件识别、集合判重

简介

Bloom Filter是一个占用空间很小、效率很高的随机数据结构，它由一个bit数组和一组Hash算法构成。可用于判断一个元素是否在一个集合中，查询效率很高（1-N，最优能逼近于1）。

在很多场景下，我们都需要一个能迅速判断一个元素是否在一个集合中。譬如：
网页爬虫对URL的去重，避免爬取相同的URL地址；
反垃圾邮件，从数十亿个垃圾邮件列表中判断某邮箱是否垃圾邮箱（同理，垃圾短信）；
缓存穿透，将已存在的缓存放到布隆中，当黑客访问不存在的缓存时迅速返回避免缓存及DB挂掉。

可能有人会问，我们直接把这些数据都放到数据库或者redis之类的缓存中不就行了，查询时直接匹配不就OK了？
是的，当这个集合量比较小，你内存又够大时，是可以这样做，你可以直接弄个HashSet、HashMap就OK了。但是当这个量以数十亿计，内存装不下，数据库检索极慢时该怎么办。

以垃圾邮箱为例：

方案比较

1.将所有垃圾邮箱地址存到数据库，匹配时遍历
2.用HashSet存储所有地址，匹配时接近O（1）的效率查出来
3.将地址用MD5算法或其他单向映射算法计算后存入HashSet，无论地址多大，保存的只有MD5后的固定位数
4.布隆过滤器，将所有地址经过多个Hash算法，映射到一个bit数组

优缺点

方案1和2都是保存完整的地址，占用空间大。一个地址16字节，10亿即可达到上百G的内存。HashSet效率逼近O(1)，数据库就不谈效率了，不在一个数量级。
方案3保存部分信息，占用空间小于存储完整信息，存在冲突的可能（非垃圾邮箱可能MD5后和某垃圾邮箱一样，概率低）
方案4将所有地址经过Hash后映射到同一个bit数组，看清了，只有一个超大的bit数组，保存所有的映射，占用空间极小，冲突概率高。

大家知道，java中的HashMap有个扩容参数默认是0.75，也就是你想存75个数，至少需要一个100的数组，而且还会有不少的冲突。实际上，Hash的存储效率是0.5左右，存5个数需要10个的空间。算起来占用空间还是挺大的。
而布隆过滤器就不用为每个数都分配空间了，而是直接把所有的数通过算法映射到同一个数组，带来的问题就是冲突上升，只要概率在可以接受的范围，用时间换空间，在很多时候是好方案。布隆过滤器需要的空间仅为HashMap的1/8-1/4之间，而且它不会漏掉任何一个在黑名单的可疑对象，问题只是会误伤一些非黑名单对象。

原理

初始化状态是一个全为0的bit数组

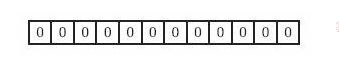
为了表达存储N个元素的集合，使用K个独立的函数来进行哈希运算。x1，x2……xk为k个哈希算法。
如果集合元素有N1，N2……NN，N1经过x1运算后得到的结果映射的位置标1，经过x2运算后结果映射也标1，已经为1的报错1不变。经过k次散列后，对N1的散列完成。
依次对N2，NN等所有数据进行散列，最终得到一个部分为1，部分位为0的字节数组。当然了，这个字节数组会比较长，不然散列效果不好。

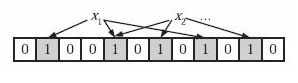
那么怎么判断一个外来的元素是否已经在集合里呢，譬如已经散列了10亿个垃圾邮箱，现在来了一个邮箱，怎么判断它是否在这10亿里面呢？
很简单，就拿这个新来的也依次经历x1，x2……xk个哈希算法即可。
在任何一个哈希算法譬如到x2时，得到的映射值有0，那就说明这个邮箱肯定不在这10亿内。
如果是一个黑名单对象，那么可以肯定的是所有映射都为1，肯定跑不了它。也就是说是坏人，一定会被抓。
那么误伤是为什么呢，就是指一些非黑名单对象的值经过k次哈希后，也全部为1，但它确实不是黑名单里的值，这种概率是存在的，但是是可控的。



上面的几个图看起来很高深，但那不是我们关心的问题，归根到底意思其实就是你想让错误率降低，就得增大数组的长度，就是这样。
我们使用BloomFilter的目的就是想省空间，所以我们需要做的就是在错误率上做个权衡就OK。
很多时候这个错误率我们是能接受的，譬如垃圾邮箱问题，是坏人一定会被抓，这个能保证。无非是一些好人也被抓，这个可以通过给这些可伶的被误伤的设置个白名单就OK。至于爬虫Url重复这个就更没问题了，会缺掉一些网页而已。
至于在缓存穿透上的应用，是为了避免恶意用户频繁请求缓存中不存在DB也不存在的值，会导致缓存失效、DB负载过大，可以使用BloomFilter把所有数据放到bit数组中，当用户请求时存在的值肯定能放行，部分不存在的值也会被放行，绝大部分会被拦截，这些少量漏网之鱼对于DB的影响就会比大量穿透好的多了。

如何判断一个元素是否存在一个集合中？

常规思路：
数组
链表
树、平衡二叉树、Trie
Map (红黑树)
哈希表
虽然上面描述的这几种数据结构配合常见的排序、二分搜索可以快速高效的处理绝大部分判断元素是否存在集合中的需求。但是当集合里面的元素数量足够大，如果有500万条记录甚至1亿条记录呢？这个时候常规的数据结构的问题就凸显出来了。数组、链表、树等数据结构会存储元素的内容，一旦数据量过大，消耗的内存也会呈现线性增长，最终达到瓶颈。有的同学可能会问，哈希表不是效率很高吗？查询效率可以达到O(1)。但是哈希表需要消耗的内存依然很高。使用哈希表存储一亿 个垃圾 email 地址的消耗？哈希表的做法：首先，哈希函数将一个email地址映射成8字节信息指纹；考虑到哈希表存储效率通常小于50%（哈希冲突）；因此消耗的内存：8 * 2 * 1亿 字节 = 1.6G 内存，普通计算机是无法提供如此大的内存。这个时候，布隆过滤器（Bloom Filter）就应运而生。

布隆过滤器—不存在肯定不存在

布隆过滤器（Bloom Filter）的核心实现是一个超大的位数组和几个哈希函数。假设位数组的长度为m，哈希函数的个数为k。

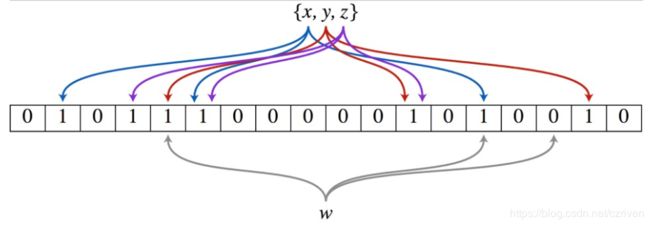
以上图为例，具体的操作流程：假设集合里面有3个元素{x, y, z}，哈希函数的个数为3。首先将位数组进行初始化，将里面每个位都设置位0。对于集合里面的每一个元素，将元素依次通过3个哈希函数进行映射，每次映射都会产生一个哈希值，这个值对应位数组上面的一个点，然后将位数组对应的位置标记为1。查询W元素是否存在集合中的时候，同样的方法将W通过哈希映射到位数组上的3个点。如果3个点的其中有一个点不为1，则可以判断该元素一定不存在集合中。反之，如果3个点都为1，则该元素可能存在集合中。注意：此处不能判断该元素是否一定存在集合中，可能存在一定的误判率。可以从图中可以看到：假设某个元素通过映射对应下标为4，5，6这3个点。虽然这3个点都为1，但是很明显这3个点是不同元素经过哈希得到的位置，因此这种情况说明元素虽然不在集合中，也可能对应的都是1，这是误判率存在的原因。

布隆过滤器添加元素

将要添加的元素给k个哈希函数
得到对应于位数组上的k个位置
将这k个位置设为1

布隆过滤器查询元素

将要查询的元素给k个哈希函数
得到对应于位数组上的k个位置
如果k个位置有一个为0，则肯定不在集合中
如果k个位置全部为1，则可能在集合中

布隆过滤器代码实现

package com.github.lovasoa.bloomfilter;

import java.util.BitSet;
import java.util.Random;
import java.util.Iterator;

public class BloomFilter implements Cloneable {
  private BitSet hashes;
  private RandomInRange prng;
  private int k; // Number of hash functions
  private static final double LN2 = 0.6931471805599453; // ln(2)

  /**
   * Create a new bloom filter.
   * @param n Expected number of elements
   * @param m Desired size of the container in bits
   **/
  public BloomFilter(int n, int m) {
    k = (int) Math.round(LN2 * m / n);
    if (k <= 0) k = 1;
    this.hashes = new BitSet(m);
    this.prng = new RandomInRange(m, k);
  }

  /**
   * Create a bloom filter of 1Mib.
   * @param n Expected number of elements
   **/
  public BloomFilter(int n) {
    this(n, 1024*1024*8);
  }

  /**
  * Add an element to the container
  **/
  public void add(Object o) {
    prng.init(o);
    for (RandomInRange r : prng) hashes.set(r.value);
  }
  /** 
  * If the element is in the container, returns true.
  * If the element is not in the container, returns true with a probability ≈ e^(-ln(2)² * m/n), otherwise false.
  * So, when m is large enough, the return value can be interpreted as:
  *    - true  : the element is probably in the container
  *    - false : the element is definitely not in the container
  **/
  public boolean contains(Object o) {
    prng.init(o);
    for (RandomInRange r : prng)
      if (!hashes.get(r.value))
        return false;
    return true;
  }

  /**
   * Removes all of the elements from this filter.
   **/
  public void clear() {
    hashes.clear();
  }

  /**
   * Create a copy of the current filter
   **/
  public BloomFilter clone() throws CloneNotSupportedException {
    return (BloomFilter) super.clone();
  }

  /**
   * Generate a unique hash representing the filter
   **/
  public int hashCode() {
    return hashes.hashCode() ^ k;
  }

  /**
   * Test if the filters have equal bitsets.
   * WARNING: two filters may contain the same elements, but not be equal
   * (if the filters have different size for example).
   */
  public boolean equals(BloomFilter other) {
    return this.hashes.equals(other.hashes) && this.k == other.k;
  }

  /**
   * Merge another bloom filter into the current one.
   * After this operation, the current bloom filter contains all elements in
   * other.
   **/
  public void merge(BloomFilter other) {
    if (other.k != this.k || other.hashes.size() != this.hashes.size()) {
      throw new IllegalArgumentException("Incompatible bloom filters");
    }
    this.hashes.or(other.hashes);
  }

  private class RandomInRange
      implements Iterable<RandomInRange>, Iterator<RandomInRange> {

    private Random prng;
    private int max; // Maximum value returned + 1
    private int count; // Number of random elements to generate
    private int i = 0; // Number of elements generated
    public int value; // The current value

    RandomInRange(int maximum, int k) {
      max = maximum;
      count = k;
      prng = new Random();
    }
    public void init(Object o) {
      prng.setSeed(o.hashCode());
    }
    public Iterator<RandomInRange> iterator() {
      i = 0;
      return this;
    }
    public RandomInRange next() {
      i++;
      value = prng.nextInt() % max;
      if (value<0) value = -value;
      return this;
    }
    public boolean hasNext() {
      return i < count;
    }
    public void remove() {
      throw new UnsupportedOperationException();
    }
  }
}

源码地址: link.