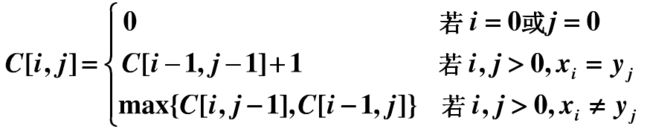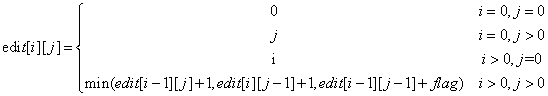动态规划面试题基础合集1--数学三角形，LIS , LCS, CSD

动态规划的一般思路是分为四步，即：寻找最优子结构、递归定义最优子结构、自底向上求解最优子结构和构造最优解。

接下来我列举出几个常见的动态规划面试题进行说明。

（1）数学三角形：比较简单，直接贴一个我看到的讲得最清楚的文章，http://blog.csdn.net/baidu_28312631/article/details/47418773

（2）LIS：最长上升子序列问题。

　　思路1：

　　其实就是寻找f(n)和f(n-1)之间的关系，对于一个序列，f(n)要么等于f(n-1),要么等于f(n-1)+1, 但是什么情况下相等，这是需要思考清楚的，也是解决这个问题的关键。

　　通过自己写一写test case，可以发现这种递推式无法很方便地写出来，因为第n个数和第n-1个数的关系无法推导f(n), 但是我们换个思路转换原问题的话，马上可以得到这样一个递推式：

　　　　　　　　　　　　　　

　　这里对问题进行了转换，变成了：序列加入一个数后，包含这个数的最长上升子序列。举个例子，如果加入的数小于序列其他值，那么显然有L(k) = 1。 这是一个递推式，我们很容易能自底向上求得L(k).

　　这个问题和原问题并不等价，但是我们可以发现既然是最长递增子序列，那么只要找到这个问题中L(k)的最大值即可。原问题的f(k) = max(L(k)) , 这个才是原问题的解。

　　思路2：（奇妙的解法，复杂度O(n*logn), 看了几篇文章发现要么不解释，要么解释很复杂，我这里简洁描述一下，应该挺好懂）

　　由于一个序列的上升子序列有很多，那么我们如何判断新加入一个数后，最长子序列是否增长了呢？我们可以记录相同长度的子序列中所有最大值的最小值，只要加入一个数，就遍历不同长度子序列的最小值，判断新加入的数是否大于这个最小值就能得到最长子序列。

　　所以，创建一个长度为n的数组来存这些不同长度的最小值，每加入一个数就进行二分搜索并更新这个数组，代码如下：

　　

int LIS(int* a, int n)
{
    int dp[n];
    const int inf = 0x7FFFFFFF;
    fill(dp, dp + n, inf);
    for(int i = 0; i < n; i++) {
             *upper_bound(dp,dp + n, a[i]) = a[i];//二分搜索，返回一个非递减序列[first, last)中的第一个大于值val的位置
    }
    return (lower_bound(dp, dp + n, inf)-dp);//二分搜索，返回一个非递减序列[first, last)中的第一个大于等于值val的位置
}

 （3）LCS:最长公共子序列问题，比如求两个字符串的最长公共字符串长度。

比如字符串1：BDCABA；字符串2：ABCBDAB

则这两个字符串的最长公共子序列长度为4，最长公共子序列是：BCBA

思路：可以推导出如下递归公式：

 

//递归解法
int LCS(const char* s1, const char* s2, int i, int j)
{
    if(i<0 || j<0)
        return 0;
    if(s1[i] == s2[j])
    {
        return LCS(s1, s2, i-1, j-1)+1;
    }
    else
    {
        return max(LCS(s1, s2, i, j-1),LCS(s1, s2, i-1, j));
    }
}
//循环解法
int LCS2(string s1, string s2)
{
    int len1 = s1.length();
    int len2 = s2.length();
    int dp[len1+1][len2+1];
    for(int i=0;i<=len1;++i)
        fill(dp[i], dp[i]+len2+1, 0);
    for(int i=1;i<=len1;++i)
    {
        for(int j=1;j<=len2;++j)
        {
            if(s1[i-1]==s2[j-1])
                dp[i][j] = dp[i-1][j-1]+1;
            else
                dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
        }
    }
    return dp[len1][len2];
}

 （4）CSD(编辑距离)：

字符串的编辑距离，又称为Levenshtein距离，由俄罗斯的数学家Vladimir Levenshtein在1965年提出。是指利用字符操作，把字符串A转换成字符串B所需要的最少操作数。其中，字符操作包括：

• 删除一个字符    

• 插入一个字符    

• 修改一个字符     

例如对于字符串"if"和"iff"，可以通过插入一个'f'或者删除一个'f'来达到目的。

思路：递推公式如下

i>0,j>0的公式分别是删除一个字符，插入一个字符，修改一个字符后的操作次数。其它的边界条件就容易理解了。递归代码如下，循环版本的也很好写。

int min3(int a, int b, int c)
{
    return min(min(a,b),c);
}

int CSD(const char* s1, const char* s2, int i, int j)
{
    if(i<0 && j<0)
        return 0;
    else if(i<0)
        return j+1;
    else if(j<0)
        return i+1;
    return min3(CSD(s1,s2,i-1,j)+1, CSD(s1,s2,i,j-1)+1, CSD(s1,s2,i-1,j-1)+(s1[i]==s2[j]?0:1));
}

 

转载于:https://www.cnblogs.com/nice-forever/p/6635425.html