深入浅出EM算法

写这篇博文用了很多时间和精力，如果这篇博文对你有帮助，希望您可以打赏给博主相国大人。哪怕只捐1毛钱，也是一种心意。通过这样的方式，也可以培养整个行业的知识产权意识。我可以和您建立更多的联系，并且在相关领域提供给您更多的资料和技术支持。

赏金将用于拉萨儿童图书公益募捐
手机扫一扫，即可：

附：《春天里，我们的拉萨儿童图书馆，需要大家的帮助》

博主博文推荐：
如果你希望能够对python有更多的掌握，可以参考博主的系列博文
《python高手的自修课》

1.概率论基础：你没见过的概率

这一部分内容与EM算法并没有太大的关系，如果你不想多学点儿东西，可以直接跳过。写这一部分主要原因是：很多学生最开始接触EM算法是通过李航博士的《统计学系方法》这本书，然而，李航博士在这本书中的推导，用的书写格式过于专业，因此，如果你不了解本一部分内容，可能阅读这本书会遇到障碍。另一方面，我们阅读的很多论文，都存在这样的障碍，如果你对这一部分已经有了很好的理解，这将会为你扫清很大的障碍。

1.1约定：

P(α1∩α2∩...∩αk) 与 P(α1,α2,...,αk) 一样，都表示 (α1,α2...αk) 的联合概率。
请不要忽略这句话的存在，今后看各种文献焦头烂额时，或许你才会体会到这句话真正的价值。来看一组练习：

P(α|β,γ)⇔P(α|β∩γ)⇔P(α|β)（在事件（参数）β的背景（条件）下）

P(α,β|γ)⇔P(α∩β|γ)⇔P(α∩β)orP(α,β)在事件（参数）γ的背景（条件）下

Note:
你需要自如的对这些进行无障碍的转换，因为在不同的论文，教材中，作者的书写习惯都不相同（就像上面两个式子中的第1个和第2个）。在接下来的环节中，为了锻炼这种自如转换的能力，我在下面的公式中，将随机采用上面的某一种表达形式。
你要学会自如地做这样的变化。在阅读某些文献的时候，公式推导可能非常复杂，书写也非常繁琐，为了便于理解和分析，你可以试着把都有的背景条件去掉（就像上面两个式子中的第3个），这样式子就会大大简化。

1.2链式法则：

P(α1∩α2∩...∩αk)=P(α1)P(α2|α1)P(α3|α1∩α2)...P(αk|α1∩α2∩α3∩...∩αk−1)

1.3贝叶斯定理

贝叶斯（你知道的版本）：

P(α|β)=P(β|α)P(α)P(β)

贝叶斯（你不知道的版本）：

P(α|β∩γ)=P(β|α∩γ)P(α∩γ)P(β∩γ)

其中所有的概率均以某个背景事件 γ 为条件。当然也可以这样写：

P(α|β,γ)=P(β|α,γ)P(α,γ)P(β,γ)

1.4独立性

第一种定义：假如 P(α|β)=P(α)orP(β)=0 ，则称 α 与 β 独立。记作： P⊨(α⊥β) 简写为 (α⊥β)
第二种定义：分布 P 满足 (α⊥β) 当且仅当 P(α∩β)=P(α)P(β)

1.5条件独立

把上一节的独立性定义中，都加上一个共同的背景条件，就变成了条件独立性。例如：
第一种定义：假如 P(α|β,γ)=P(α|γ)orP(β∩γ)=0 ，则称 α 与 β 在给定事件 γ 时，在分布 P 中条件独立独立。记作： P⊨(α⊥β|γ) 简写为 (α⊥β|γ)
第二种定义：分布 P 满足 (α⊥β|γ) 当且仅当 P(α∩β|γ)=P(α|γ)P(β|γ)

条件独立有什么实际意义呢？事实上，在现实生活中，我们很少会碰到两个相互独立的事件。一种更为普遍的情况是，两个事件在给定额外事件的条件下独立。例如，假定要推理某学生被东南大学（SEU）或者南京大学（NU）录取为研究生的机会。在许多合理的分布中，这两个事件并不独立。因为，如果已知一个学生已经被南京大学录取，那么我们对他被东南大学录取的概率估计就会提高。因为他被南京大学录取说明他是一个比较有前途的学生。
现在，假定这两所大学都只根据本科成绩GRAD做决定，且只根据这个做决定。并且已知学生的本科成绩是A，那么在这种情况下，我们发现，已知这个学生被南京大学录取并不会改变他被东南大学录取的概率。因为两个学校都只根据GRAD来录取。也就是说，他的成绩已经显示出他被东南大学录取的相关信息，并且他被南京大学录取的事实并不会改变现状。用公式表示为：

P(SEU|NU,GRAD)=P(SEU|GRAD=A)

对于这种情况，我们就说，在给定 GRAD=A 的条件下， SEU 与 NU 条件独立。

1.6随机变量独立性性质

1.6.1对称

(X⊥Y|Z)⇒(Y⊥X|Z)

1.6.2分解

(X⊥Y,W|Z)⇒(X⊥Y|Z)

这个式子看糊涂了没？看糊涂的话，请返回第1小结的 Note。
接下来，相国大人带你分析这玩意儿吧：
原式相当于（非严格）：

(X⊥(Y∩W))⇒(X⊥Y)

意思就是说， X 与两个事件的联合独立，则其与联合中任何一个分量都独立。
WHY？
证明（这里把 W 写成了 M ，笔误）：

1.6.3弱联合

(X⊥Y,W|Z)⇒(X⊥Y|Z,W)

又看不懂了？请返回第1小结的 Note
接下来，相国大人带你分析这玩意儿吧：

(X⊥Y,W)⇒(X⊥Y|W)

证明：

1.6.4收缩

(X⊥W|Z,Y)∩(X⊥Y|Z)⇒(X⊥Y,W|Z)

证明（以后更新）：
精力实在有限，这部分没时间去证明了，有做好的同行，欢迎发给我，我粘贴到这里。

1.6.5相交

对正分布（如果对于所有事件 α≠0,α∈S , P(α)>0 成立则称 P 为正分布），以及互不相交的集合 X,Y,Z,W ：

(X⊥Y|Z,W)∩(X⊥W|Z,Y)⇒(X⊥Y,W|Z)

证明（以后更新）：
精力实在有限，这部分没时间去证明了，有做好的同行，欢迎发给我，我粘贴到这里。

2.琴声不等式

Jensen不等式在优化理论中大量用到，首先来回顾下凸函数和凹函数的定义。假设 f 是定义域为实数的函数，如果对于所有的 x ， f(x) 的二阶导数大于等于0，那么 f 是凸函数。当 x 是向量时，如果海森矩阵H是半正定（即H>=0），那么 f 是凸函数。如果 f(x) 的二阶导数小于0或者H<0，那么 f 就是凹函数。

Jensen不等式描述如下：
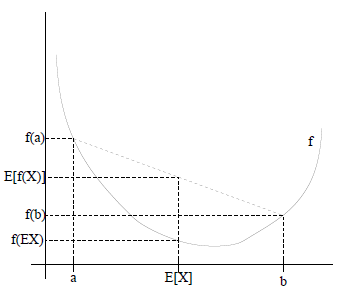
1，如果 f 是凸函数，X是随机变量，则 f(E[X])⩽E[f(X)] ，特别地，如果 f 是严格凸函数，那么等号成立当且仅当 P(x=E[X])=1 时（也就是说X是常量）；
2，如果 f 是凹函数，X是随机变量，则 f(E[X])⩾E[f(X)] ，，特别地，如果 f 是严格凹函数，那么等号成立当且仅当 P(x=E[X])=1 时（也就是说X是常量）；
3，当 f 是（严格）凹函数当且仅当-f是（严格）凸函数。

通过下面这张图，可以加深印象：

上图中，函数 f 是凸函数， X 是随机变量，有0.5的概率是 a ，有0.5的概率是 b 。 X 的期望值 E(x) 就是 a 和 b 的中值 (a+b)/2 了，图中可以看到 E[f(X)]⩾f(E[X]) 成立。

本文在第四节EM算法导出中，会用到这个不等式性质，在那一节，我们公式中的 X 是一个函数。这个函数是：

X:g(z)=p(x,z;θ)Q(z)

你不必理解这个函数的具体意思，这里只是混个脸熟就好。如果告诉你这个函数是凹函数，那么，你应该理解：

f(E[p(x,z;θ)Q(z)])⩾E[f(p(x,z;θ)Q(z))]

进一步的，如果告诉你 Q(z) 是 z 的概率，那么仅仅根据本科的知识，你也应该知道:

E[p(x,z;θ)Q(z)]=∑zQ(z)p(x,z;θ)Q(z)

如果对这个式子看了好久还是没有明白，那么博主建议你放弃机器学习这个行业。

3.坐标上升方（坐标下降法）

坐标下降法是一种对多个参数分步迭代最终得到目标函数局部极大值（极小值）的方法。具体来说，对于目标函数： f(μ,θ) ，我们首先给定一个最初的猜想值 θ0 ，则：

μ1=argmaxμf(μ,θ0)

θ1=argmaxθf(μ1,θ)

μ2=argmaxμf(μ,θ1)

θ2=argmaxθf(μ2,θ)

...

显然，一定有 f(μ1,θ0)⩽f(μ2,θ1)...⩽f(μi+1,θi)⩽fmax 。随着迭代的持续进行， f(μi+1,θi) 将逐渐逼近为 fmax ，此时 θi 和 μi+1 即为我们的参数估计。本文在第四节中将会用到这一方法。当然，对于更多的参量，坐标下降（上升）法的迭代规则可以参考这个公式：

xt+1i=argminyf(xt+11,xt+22,...,y,xti+1,...,xtd)

4.EM算法导出

到这里，我们才算真正进入到了EM算法的门口了。EM算法之所以学习起来感到困难，一方面是我们忽略了几本的概率知识，另一方面，对于刚开始接触机器学习的人来说，还不习惯迭代的这种思想。导出的方法多种多样，博主选择从零开始，一点一点，用最通俗易懂的方法来进行推导。
博主的目标是：让零基础，没学过机器学习的人也可以看懂。这个目标的实现有一下几个前提：

1. 你已经对前三节有了一个比较靠谱的理解和吸收。
2. 你能够回忆一些本科概率统计中关于极大似然估计方面的知识。如果你回忆已经很模糊也没有关系，你可以重新找这个部分的教材看一下，我接下来也会讲到。

我将按照下面的顺序进行讲解：

1. 从最大似然估计MLE说起
2. 我们遇到了什么问题？
3. EM算法的导出
4. 网络上流行的几个导出版本
5. 深入之后，让我们浅出一下
   接下来，让我们开始激动人心的探险之旅吧！

4.1 从最大似然估计MLE说起

现实生活中，我们解决问题的一个常用思路是：

1.第一步：在这个问题中，我们可以观测到哪些特征呢？不妨把它们叫做 x(1),x(2),...,x(n ，每一个特征都有自己的取值。这样一来我们可以把这些特征统称为 X ,其中 X={x(1),x(2),...,x(n} 。我们会重复很多次实验，观测到很多结果。因为每次实验都是独立操作的（例如你今天摸彩票和你明天摸彩票没关联，但是你每天都去摸，那么一个月下来后，你就得到了30个观测样本。）于是我们可以得到一系列独立同分布的样本点。

相国大人倾情补充：
什么是独立同分布？
就是每天去摸彩票之间是没关联的不会因为你昨天没中奖，今天就能中，但是每天中奖的概率都是遵循都一个概率分布函数，注意是同一个，同一个，同一个。重要的事情说三遍。我们来看一个例子：
这是某一个概率分布 P(X) ，每一次做实验都由它产生了样本点 x1,x2,x3...xn 。我们用大写 X 来表达 X 可以是 xi 中的任何一个， X 被叫做随机变量。 xi 表示每一次实验的样本（观测到的结果），注意这是一个特征向量不要和这个混淆 x(1) ，这个是特征。例如 x=(x(1),x(2),...,x(k)) ,其中 x(1) 也许表示的是肤色， x(2) 也许表示体重……你或许已经发现了，这些样本点，其实就是这些特征构成的特征空间中的点。这些点组成的整体的形态，就是这个概率分布规定的。我们不妨姑且假设这个概率分布产生的样本点，在特征空间中是一个球（随便胡诌的）
现在有另一个概率分布 P′(X) 它产生了另外一组样本点 x′1,x′2,x′3...x′n 他在这个同样的特征空间中，产生了另一群样本点，这群样本点也有自己的形态（姑且是一个椭球吧）
我们知道所有样本点都是独立做一次实验的结果，跟前一次实验结果没有关系，因此我们说这些点都是独立的。但是 x1,x2,x3...xn，x′1,x′2,x′3...x′n 这些样本点不是同分布。他们分别属于两个分布。这就是独立同分布的一个直观的解释。
当然，好奇的你也许会问，这个空间中，有一个椭球，有一个球，他们各自是同分布的，彼此不是。而且刚才您也说到，他们的形态是有各自的分布规定的。那么我可不可以把这种位置不变的椭球体加球体的组合看做是一个联合体（整体），并把它叫做“相国大人体”呢？答案是可以的，那既然我们把它看做了一个新的几何体。它自然也有自己的概率分布 P′′(X) ，这个玩意儿能求吗？
能求。而且事实上，这个玩意儿已经求出来了：

P′′(X)=weight1P(X)+weight2P′(X)

其实就是两个类别分布的加权组合。那么这个权值又是什么呢？聪明的你，知道吗？
既然是联合了，那么我每次做实验时，就要考虑一个问题，这次实验，老子是要做第一个呢？还是第二个呢？这是一个问题，不妨我们弄个概率模型 P′′′(Z),Z={"first","second"} ，随机生成一个吧，生成那个，俺就做哪个。于是这个权值，就是选择做第1（2）个实验的概率。换句话说，就是这个样本点是来自第一（二）个分布的概率；换句话说，就是这个样本点属于第1（2）类的概率；换句话说，就是这个样本点隐含的类别；话句话说……

接下来，为了让你不二胡，我们再强调一下书写：不同的样本点用下标表示，上标 (i) 表示是某一个特征。换句话说下标是特征空间的某一个点，上标是这个特征空间的坐标轴。某一个 xi=(x(1),...x(n)) 所对应的具体的 x(i) 是这个点的坐标值。 累死本大爷了。

2.第二步：我们会根据自己的学识，对这些个 x(i) 进行建模，我们的模型中会有一些参量，不妨把它们叫做 θ （特别的，如果是多个参量，那 θ 就是一个向量 θ=(θ1,...θk) ）。问题是我们应该建立什么模型呢？一种最通俗易懂的模型就是建立这些特征的联合概率。即：

P(x(1),x(2),...,x(n)

不要对这个式子“感冒”哦，在第一节我说过，这个式子其实就是：

P(x(1)∩x(2)∩,...,∩x(n)

为什么要这么建模呢？你问过自己吗？
没问过，说明你不会学习。
通俗地说，这种建模非常符合人类对事情的认知。
例如，我们研究一个问题，只能得到观测的数据，这些观测数据，就是一系列的 X ，进一步的说，这些观测数据，就是一系列的 x1,...,xn 取值的组合。人类看到天上有星星，于是就问自己，为什么我会看到这些星星而不是那些星星呢？于是产生了地心说和日心说。我们看到一种现象，就会思考为什么出现的是这个现象，而不是另一个现象。为什么 (x1,...,xn) 是 (0,1,...,"周一","小红") 而不是 (1,0,...,"周二","小绿") 呢？于是我们很自然的希望能够得到一种特定组合发生的概率，也就是我们的这个联合概率:

P(x(1),x(2),...,x(n)公式(1)

3.第三步:已知我们已经做了n次实验，得到了n个样本点 x1,x2,...xn 上面的公式1是每一个样本的概率，请注意公式（1）也可以写成这个样子： P(x) 。现在我们独立做了n实验，我们不禁在想，为什么是这样一种结果的组合，而不是另一种结果的组合呢？（这个思想如果你还没有理解，请返回第2步）于是我们用上面的概率构造了另一个概率(请注意下标！)：

P(x1,x2,...,x3)=P(x1)P(x2)...P(xn)（注意xi相互独立）

准确来讲，这个东西是一个值，我们已经知道的值。因为这里的 xi 都是我们观测的结果，是已知量。而这个 P（⋅） 是我们自己建的模型，也是已知的。也就是说，如果我们的模型里面没有未知参数 θ ，这玩意儿就求出来了。但是正是因为模型里面有 θ 所有我们的这个式子里面有 θ 。于是你会发现，这个玩意儿是关于 θ 的一个函数，不妨把它叫做 L(θ) 吧。走到这一步，完事具备，只欠“ θ ”了，于是我们开始基于训练数据，也就是已有经验来对参数进行估计，我们把这一步叫做“学习”。参数稳定后，接下来，给定一个观测点 X ，我们就可以预测它的类别了（如果你建立的模型是为了这个的话），或者我们的模型是一个联合概率，这样我们可以预测某一种组合状态发生的概率。
现在的问题是该如何估计呢？
一般情况下，如果幸运，我们的模型就是输入 X （这个是我们的观测值，是已知量）与参数 θ 之间的那点恩怨纠葛。我们可以假定联合概率取最大时，应该用什么参数，来得到参数的估计。更准确地说，就是 θ 应该取得什么值，才能使得无论输入 X 如何，得到的联合概率都是这一特定输入下的最大的概率了呢？ 换句话说，现在我们有这n个样本点，我们要估计 θ （注意，是估计！），我们该如何让上帝相信我们估计的 θ 是最可靠的呢？事实胜于雄辩，我们告诉上帝，你用我这个 θ ，出现这种观测结果的概率是最大的。于是上帝明白，哦，看来用这个参数值是最有可能出现这种现象的。换句话说，就是这个联合概率 L(θ) 关于参数 θ 取得最大值时，对应的 θ 。一种本科小屁孩儿都知道的方法就是将这个联合概率对 θ 求偏导数，令其为零。Are you understand?
是的，就是这么个破玩意儿，还有个专有名词，叫做“ 最大似然估计”。

相国大人温情补充：
具体来说，我们把这个联合概率关于参数 θ 的函数叫做似然函数：

L(θ)=P(x1,x2,...,xn;θ)

需要注意的是，这里我们用分号把 xi 和 θ 进行了分隔，在李航博士《统计学系方法》和《概率图模型》等著作中，人们是用”|”来进行分隔的。当然，不嫌事儿多的你，也许喜欢更刺激的表达方式：

L(θ)=P((x11,x21,...,xk1),(x12,x22,...,xk2)...,(x1n,x2n,...,xkn);θ)

我们更为常用的似然函数形式是对这个联合概率取对数，即更为常用的似然函数是：

L(θ)=logP(x1,x2,...,xn;θ)

不知你有没有想过为什么？
如果不取对数，那么我们的似然函数就是若干概率的乘积。每一个概率都是小于1的数。如果有100个样本点，那么最终得到的结果几乎就为0了。任何一门编程语言，都不太可能保证如此精确的计算。我们把这个叫做“下溢”。当然，另一方面，也是因为取对数计算更简单。
考虑到我们观测的样本点都是相互独立的，因此可以进一步写成：

L(θ)=∑ilogP(xi;θ)

如果你看了上一段我说的那个 和上帝对话的比喻的话，你也许就会知道为什么把它叫做“似然”了吧：
“然”在古汉语中，常常用做形容词，表示“对的”。（“诚然”）
“似”，在古代汉语中，常常用作副词（修饰限定形容词、动词的词），表示“似乎，好像”（白发三千丈，缘愁似个长。）
因此似然值可以表达为“似乎是对的值”，用来求似然值的函数，就叫做“似然函数”了。
不要问我从哪里知道的。我说过，这篇博客的名字叫做《深入浅出EM》，如果你感激我，别整那些没用的，直接扫我 支付宝捐款（在开头），其他的都是虚的。
此处看不懂，尔等可缓缓归矣。

4.2 我们遇到了什么问题？

极大似然估计这玩意儿是真好啊，解决了不少问题，但是有一种情况，它玩儿完了。
我们刚才说到，如果幸运，我们的模型就是输入 X （这个是我们的观测值，是已知量）与参数 θ 之间的那点恩怨纠葛。但是如果模型的输入不仅仅有 X ，还有某些我们观测不到，但是确实存在的”影子”输入 z 呢？
这种情况下，我们想像以前一样对这个联合概率做 θ 偏导，可是人们发现，这个偏导数求不出来。为什么求不出来呢？你看到过的所有资料，对这个问题都是一笔带过，是吧？接下来，让我来为你刨根究底：
假设概率模型为 P((x(1),x(2),z);θ) ，其中 (x(1),x(2),z) 是一个三维的特征向量，由于某种原因，我们只看到了 x(1),x(2) 这两个特征，没有观测到 z 这个特征。 (x(1),x(2),z) 构成了一个三维的样本空间，我们做的n次实验结果，是根据这个概率模型分布生成的点。如下图（这个图是我用python做的一个示意图，生成的是随机点，当然你也可以按照某个概率模型来生成点，但是从说明的功能上看，这个示意图已经足够了。如果你对我这个图比较感兴趣，可以在这篇博文中，找到代码）：

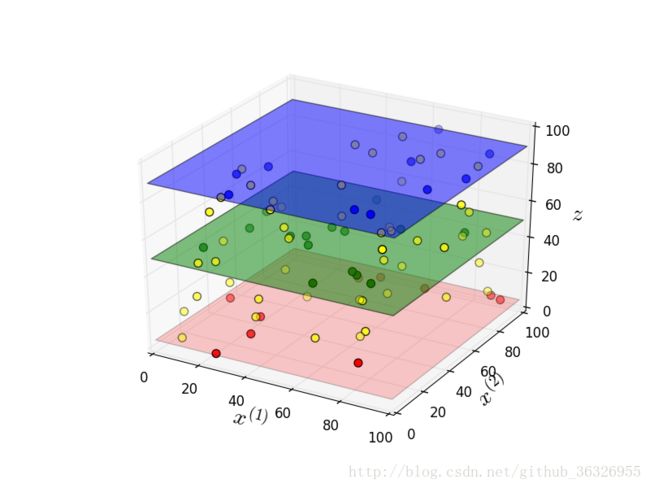
看不清楚的话，再换个角度：

一位浙大的博士提出，我这个图有问题，就是z轴不应该与x，y垂直。因为垂直意味着z与x，y没有信息交互。我觉得这种说法是有道理的。在此表示感谢。但是为了让大家有一个直观的印象，我想，还是暂且沿用这个图吧。空间所有的点，都是由 P((x(1),x(2),z);θ) 这个模型生成的，这个模型规定了这些点在三维空间内的形态。但是对于每个平面中的点而言，他们在这个平面中也有一个形态，这个形态是由位于这个平面上的二维概率模型 P′((x(1),x(2));θ) 规定的。这个 P′ 与那个 P 是不同的分布。一个是三维，一个是二维。由于你看不到 z ,因此这些样本点，在你看来，是这样的：

于是你会发现，我们仅仅基于二维特征，得不到第三个维度 z 的特征。
如果你对这句话还存在怀疑的态度，那么我们下面用数学式子，来为你推一下：
我们首先设红，绿，蓝三个平面上的概率分布为 P(1),P(2),P(3) ，每个 z 平面上出现的样本点个数分别为 k1,k2,...km ,换句话说，这 k1,k2,...km 的和是样本点总数 n ，而下标 m 正好是这些样本点对应的所有不同 z 值的个数，换句话说就是这些样本点对应着 m 个 z 平面。那么前面说的似然函数可以写成：

L(θ)=P(x1,x2,...,x3)=P(x1)P(x2)...P(xn)

其中 P(xi)=∑mk=1P(z=zk)P(k)(xi)
即：

L(θ)=∏i=1n(∑k=1mP(z=zk)P(k)(xi))

这里面的 P(i)(xk) 更为准确的表述应该是：

P(i)(xk|z=zi,θ)

但是，如果你看过我在第一章写的Note的话，并且如果你跟着我也看了一下第一章那几个独立性性质的分析的话，我想你应该不会对这样的书写感到吃惊。
进一步地，我们把似然函数换成对数似然函数可以写成：

L(θ)=∑xlog(∑zP(z)P(x))

这里面的 P(x) 更为准确的表述应该是： P(x|z,θ) ，而 P(z) 应该写成 P(z|θ) 。由于 log 里面的和号中，每一项都是确定的一个 z ，因此，对于这两个概率而言，表达式里面是没有z的，而是一个含有 θ 的表达式。并且，给定某一个 z ，这两个概率我们一般也都是知道的（ 请注意我的表述：我说的是给定一个z，换句话说我要想得到这两个概率，就必须要知道这个z是什么。）。为了不让你迷糊，我这里重写一下：

L(θ)=∑xlog(∑zP(z|θ)P(x|z,θ))

按照极大似然估计的方法，我们接下来要做的是求偏导数：

∂L(θ)∂θ=∑x⎧⎩⎨∑z[P(z|θ)∂P(x|z,θ)∂θ+P(x|z,θ)∂P(z|θ)∂θ]∑zP(z|θ)P(x|z,θ)⎫⎭⎬

这里面有两点需要注意：
第一：这个式子令其为0后，求解是否复杂？我想，不用我说，你也知道，这个计算是很复杂的。但这不是主要问题。主要问题是：
第二：仔细看一下上面的式子。我们希望令这个式子为0，解出 θ ，但是从这个式子我们发现，如果我们不知道 z 有几种，上面的和式就没办法展开（写不成实际的表达式）。即便我们知道z的种类，可以展开这个和式，里面的 x 到底是哪一个样本的 x ?我们也不知道。如果这两个你都知道。。。那还叫隐变量吗？（那样的话，我们就绕回去了，可以写出具体的式子，这就变成了极大似然估计了。）也就是说，我们至少要知道z的情况，即z有多少个取值？每种取值下对应的 P(z|θ) 为多少？然而遗憾的是，我们在实际的实验中，并不能观测到z的特征，或者说，即便我们知道z的取值，我们也不知道每一个样本对应的是哪一个z。因此上面的式子，看起来有路可走，实际上是死路一条，写不出具体的式子来。这也是为什么很多教材上说“没有显示的表达式”。说的就是这个意思。

抛开繁琐的推理，让我们回到上面的那张特征空间图。
我们的样本特征有: x(1),x(2),z 。这些特征构成了一个三维的立体特征空间，每一个样本都是空间内的一个点。假设我们现在得到的数据是根据这样一个概率分布得到的 P(x(1),x(2),z) ，那么这些点将会以一种特定的“排兵布阵”弥散在这个三维空间中。很遗憾，我们现在观测不到 z ,只能看到 x(1),x(2) ，那么，这些点组成的”阵型”，在我们看来，不过是平面上的投影（也就是第3张图的视角）。
请回顾前面一节我反复提到的独立同分布这个问题。我们要估计三维概率分布的参数，就要用这个三维空间内所有的样本点来估计。我们要估计某个平面上的概率分布参数，就只能用这个平面上的样本点来估计。这就是同分布的条件。问题是，现在给我们一些点，我们搞不清哪些点是同一个平面的。如果我们蛮横地用所有点去估计一个平面上的二维概率分布，200%是错的。这就好比，你拿美国佬的饮食习惯来估计南京居民的饮食习惯，取错了地方。

一个样本集合的元素是从多个概率分布中得出的话，某个元素只可能是一个概率分布的结果，但是我们不知道这个元素从哪个概率分布中得出。所以，我们不仅要求出多个概率分布的最佳参数，而且要求出多个概率分布在模型中的比例。
而如果我们知道样本集合中的一个个元素是从哪个概率分布得出的，那直接运用极大似然估计就可求出多个概率分布的最佳参数，进而求出概率分布的比率。反过来，如果我们知道这些概率分布的最佳参数，那么我们也知道样本集合中的一个个元素分别对应哪个概率分布，也能求出概率分布的比率。于是，我们陷入了“鸡生蛋蛋生鸡”的死循环了。

截止到目前，我们终于彻底搞清了EM算法的前提。别得意的太早，接下来，才是真正开始推导EM算法的环节：

4.3 EM算法的导出

截止目前，我们其实已经介绍了两种参数估计的方法。一个是坐标下降法。另一个就是上一节的极大似然估计。那么，这两种方法什么时候，用哪个呢？
以函数 L(θ) 为例，我们会首先考察这个这个函数对 θ 求偏导。如果这两个偏导数都能够求出来（即存在偏导数）,并且都可以令其为0时，我们就得到了等式。这样就可以求得这个参数。对于凸函数而言，这个参数也必然是其极大似然估计值。但是，就像上一节我们遇到的那样。当存在隐变量时，我们得到的等式其实是个“中看不中用”的家伙。这个时候，我们可以做一个好玩的变化：
首先，我们知道这个函数有一个参数，我们希望通过某个确定的关系，再构建一个参数。不妨叫做 μ ，这样原来的函数就变成了 L(μ,θ) 。这样我们就可以用坐标下降法，假定某一个未知数的初始值，然后以此来估计另一个未知数。反复交替，也可以完成对参数的估计。也就是说，我们之所以想到要构建这样一个参数，纯粹就是为了套用坐标下降法的。
眼下的问题是，这个参数改怎么构建呢？
回顾一下坐标下降法：

μ1=argmaxμf(μ,θ0)

θ1=argmaxθf(μ1,θ)

μ2=argmaxμf(μ,θ1)

θ2=argmaxθf(μ2,θ)

...

我们发现， 当前时刻的 μi+1 其实它的式子里包含的是上一个时刻的 θi ，那么对于我们的似然函数而言，我们也可以构造一个函数 Q ，使得 μi+1=Q(θi)

还记得我们似然函数长什么样子吗？：

L(θ)=∑xlog(∑zP(z|θ)P(x|z,θ))

我想你已经注意到了，这个 log 里面有个和号，这很不好。再次强调，log里面的和号中每一项，都没z啥事儿（因为每一项都针对的是一个确定的z），这个概率都只是 θ 的参数。但是，由于有了这个和号，使得我们的log总是受到z的限制。
现在，我们引入一个新的概率 P(z|x,θ) ,很显然，这个概率表达的含义是，给定一个样本，判断它属于某一类（z）的概率，这也恰恰是我们不知道的。但是我们突然发现，这个东西里面含有 θ 并且，它还是一个不知道的。那我们就把它当做我们苦苦寻找的那个 Q 吧！
从刚才的分析中，我们已经确定了这么几个东西：
1，这个 P(z|x,θ) （也就是我们的 Q ）是对于给定的 x 和给定的 z 而言的，因此，它其实是一个含有 θ 的式子,只不过这个式子我们不知道罢了。
2，这个Q中的 θ 应该是上一时刻的 θ

如果你对于这两个东西都已经信服，那么接下来的工作就好办了。我们把Q引进到似然函数中，可以得到这样的等价变换：

L(θ)=∑xlog⎛⎝⎜∑zP(z|x,θ(i))P(z|θ)P(x|z,θ)P(z|x,θ(i))⎞⎠⎟

对于这个式子中 θ 的上标问题，我想，你应该没有疑问了吧。
我们把它用一下琴声不等式，希望把里面的和号拿到外面。关于这个地方的具体操作和推导，我已经在琴声不等式那一节的末尾给你说过了，在那里，我们的 Q(z) 其实就是 Q(z|θ) 你可以回过头来再看一下。这里我直接给出结论：

L(θ)=∑xlog⎛⎝⎜∑zP(z|x,θ(i))P(z|θ)P(x|z,θ)P(z|x,θ(i))⎞⎠⎟⩾∑x∑z⎛⎝⎜P(z|x,θ(i))logP(z|θ)P(x|z,θ)P(z|x,θ(i))⎞⎠⎟

不等式右侧，我想你已经很清楚了，它就是一个含有 θ(i) 和 θ 的式子。并且他俩儿相差一个时刻。我们不妨令:

P(z|x,θ)=μ

令不等式右侧的的部分为:

B(μ,θ)

则有：

L(θ)⩾B(μ,θ)

那么接下来我们希望通过对 B(μ,θ) 运用坐标下降法，来得到 B(μ,θ) 取极大值时的 μ,θ 。如果能证明 B(μ,θ) 取极大值与似然函数极大值相等（换句话说，就是迭代收敛到 L(θ)max ），那么我们就完成了 用坐标下降法来最大化对数似然函数下界,从而得到对数似然函数取得极大值时的参数估计,也就是极大似然估计的过程。
关于收敛性的证明，将会放到后面，我想即便我不证明，你也能感觉出来，收敛是明摆着的嘛：）

在开始我们的迭代之前，我们先来研究一个问题，就是 L(θ)⩾B(μ,θ) 这个式子，什么时候取得等号？
其实，在琴声不等式那一节，我已经说过了，对于 f(E[X])⩾E[f(X)] ，取等号的充要条件是 X 为常数。对应到我们的这个式子中来，就是： P(z|θ)P(x|z,θ)P(z|x,θ(i))=c 即：

P(z|θ)P(x|z,θ)=cP(z|x,θ(i))

两边对 z 取和式得到：

∑zP(z|θ)P(x|z,θ)=c∑zP(z|x,θ(i))

即

∑zP(z,x|θ)=c∑zP(z|x,θ(i))

看到这里，你是不是后悔自己没有好好看我的第一章呢？如果这里你二胡了，我建议你回到第一章。看看我都语重心长地对你说了什么。
这个不等式左边是x的概率。右边则为常数c即：

P(x|θ)=c

注意： ∑zP(z,x|θ)=P(x|θ) ， ∑zP(z|x,θ(i))=1 ，如果这两个你没看懂。博主给你的建议是：放弃治疗。你不适合机器学习。
紧接着我们立即可以得到：

P(z|x,θ(i))=P(z,x|θ)c=P(z,x|θ)P(x|θ)

最右侧的部分是贝叶斯定理，我在第一节说过。于是立即得到：

P(z|x,θ(i))=P(z,x|θ)P(x|θ)=P(z|x,θ)

这个式子告诉我们，当 θ 取值为 θ(i) 时，我们有 L(θ(i))=B(θ(i),θ(i)) （这里 B(μ(i),θ(i)) 我写成了 B(θ(i),θ(i)) ，都一个意思，你懂吧。）

这样一来我们就 明白了一个事情： L(θ) 与 B(θ(i),θ) 其实是下面这个图表达的关系：

这个图是从网上博客（见参考文献）粘贴过来的，所以函数名字和我的不一样。在这个图中，红线表示的是 L(θ) ，蓝色，绿色表示的分别是 B(θ(t),θ) 和 B(θ(t+1),θ) 也就是说 B(θ(t),θ) 在 θ(t) 处与 L(θ) 相等，即 L(θ(t))=B(θ(t),θ(t)) ，而在其他地方则严格小于，绿线同理。我们对 B(θ(t),θ) 采取坐标下降迭代的过程，就是下界函数有蓝线不断转移到绿线的过程。为了让你清楚的理解这个迭代过程，我们讲一下具体的操作：
初始时刻假定 θ(0) ，于是立即可以得到 μ(1)=P(z|x,θ(0)) 。这样

θ(1)=argmaxθB(μ(1),θ)

μ(2)=argmaxθB(μ,θ(1))

对于上面这个式子，我们可以直接得到 μ(2)=P(z|x,θ(1)) 想一想为什么？
我们刚才已经证明过， L(θ(1))⩾B(μ,θ(1)) ，也就是说，你 B(μ,θ(1)) 最大也就只是 L(θ(1)) 而只有 μ(2)=P(z|x,θ(1)) 的时候，等号才成立（因为此时函数 B 为 B(μ=P(z|x,θ(1)),θ(1))=B(θ(1),θ(1)) ）。所以以后不再说明，你应该知道了我们的迭代策略为：
E步：

μ(i)=P(z|x,θ(i−1))

M步：

θ(i)=argmaxθB(μ(i),θ)

以上就是我们EM算法推导的主要内容。我们“深入”的工作基本结束，接下来该“浅出”了：

“EM算法可以看做用坐标下降法来最大化对数似然下界的过程。”
——周志华《机器学习》第163页。

4.4 最后一点小尾巴

我们刚才运用 L(θ(1))⩾B(μ,θ(1)) 和 B(μ=P(z|x,θ(1)),θ(1))=B(θ(1),θ(1))=L(θ(1)) 成功的将E步做了可行性的化简。其实对于M步，我们也可以进一步地化简，这样有利于真正使用。
我们看到，在M步中，我们的式子实际上是这样的

θ(i)=argmaxθB(μ(i),θ)=argmaxθ∑x∑z⎛⎝⎜P(z|x,θ(i))logP(z|θ)P(x|z,θ)P(z|x,θ(i))⎞⎠⎟

其实，在这一步，我们的 P(z|x,θ(i)) 是个已知量。对于求最大似然估计，并没什么卵用。所以我们可以省去对 θ 的极大化而言是常数的项。则可以化简为：

θ(i)=argmaxθ∑x∑z(P(z|x,θ(i))logP(z|θ)P(x|z,θ))

网友问题解答：
有网友问为什么只把log分母去掉，而不把log前面相同的因子也去掉？
其实，提出这个问题，说明大家还没有理解这其中的本质。我们不妨把log里面的分式写成log相减的形式，则有下面的公式：

argmaxθ∑x∑z⎛⎝⎜P(z|x,θ(i))logP(z|θ)P(x|z,θ)P(z|x,θ(i))⎞⎠⎟=argmaxθ∑x∑zP(z|x,θ(i))log[P(z|θ)P(x|z,θ)]−∑x∑zP(z|x,θ(i))logP(z|x,θ(i))

其中最后一项是常数，因此去掉。

事实上，很多教材都把这个化简后的函数叫做 Q(θ(i),θ) 。因此我们最终的迭代策略为：
E步：

μ(i)=P(z|x,θ(i−1))

M步：

θ(i)=argmaxθQ(θ(i),θ)

其中

Q(θ(i),θ)=∑x∑z(P(z|x,θ(i))logP(z|θ)P(x|z,θ))

在第五节中，我们将运用这个东西，来做一个实战，推导一下高斯混合模型的参数估计。

4.5 EM算法收敛性证明

很简答，略

5.EM算法与高斯混合模型学习

我看过很多类似的博客和书籍，非常的差异。好端端的，优美的东西，让这群人推导得如此眼花缭乱。要么就是抄的并且自己没搞懂，要么就是故弄玄虚彰显情怀。在这里，你将会看到，我的推导是非常清晰和易于理解的。为了达到这个目的，我付出了很多。如果 你觉得有所收获，可以给我捐款，资助一个弱小的心灵。
首先讲一下什么是混合高斯模型，报告老师，就是这个玩意儿：