数据结构和算法之六:贪婪和动规算法
算法理论之贪婪算法和动态规划
本篇文章,简单的介绍一下贪婪算法和动态规划,因本人是算法渣渣,因此权当大家看个热闹。
贪婪算法
一个简单的问题:公司有N个同等级的会议需要使用同一个会议室,现在给你这个N个会议的开始和结束
时间,你怎么样安排才能使安排最多场次的会议?
大家先花两分钟,脑海里面梳理一下解题思路。
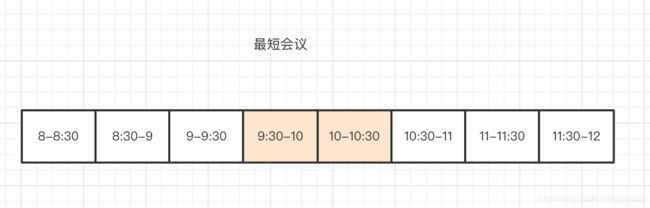
思路1:优先安排会议时间最短的能不能行?
比如时间是8-12点,会议1是9点半到10点半(1个小时),会议2从8点到10点(2个小时),会议3从10点到11点30分(1.5个小时),此时如果优先安排最短的会议,你会发现只能安排一场(会议1),但实际上会议2和会议3也能安排下去。
思路2:优先安排最早开始的会议能不能行?
这个我想相信不用举例子你就能明白,肯定是不得行的。
思路3:优先安排会议结束时间最早的能不能行?
优先安排会议结束时间最早的,那么首先将所有会议按照结束时间排序,结束时间越早的约优先安排,这样我不管以后还能不能安排会议,我只管越早结束,留下的时间就越多,能安排的会议就越多。这种是可行的,你可以多举例来证明。
我们用代码实现这个会议调度功能:
/**
* 会议调度问题
*
* 有一会议室,可接受早上8点到晚上6点这个时间段的会议,现有若干场会议需要召开
* 问,如何安排会议才能让召开的会议场次最多?
*
* 贪心算法,局部最优解推导出全局最优。
* 特点:在一定的限制中,求最值。
* 套路:一定有个一排序
*
*
* 解决思路:
* 如果先召开最早结束的会议,那么剩下的时间也就越多,能够召开的会议也就越多。
* 这样将会议进行排序,结束时间从小到大排序。
*
*/
public class MeetingSchdule {
public static void schedule(List<Meeting> meetings, int minTime, int maxTime){
if (meetings==null || meetings.isEmpty()) {
return;
}
//结束时间从小到大排序
meetings.sort((o1, o2) -> o1.endTime > o2.endTime ? 1 : -1);
final int[] curIdleBeginTime = {minTime}; //当前会议室空闲的开始时间点
meetings.forEach(meeting -> {
if(meeting.startTime >= curIdleBeginTime[0]){
System.out.println("举行会议:"+meeting);
curIdleBeginTime[0] = meeting.endTime;
}
});
}
public static void main(String[] args) {
List<Meeting> meetings = new ArrayList<>();
meetings.add(new Meeting(1, 8,9));
meetings.add(new Meeting(2, 9,10));
meetings.add(new Meeting(4, 9,11));
meetings.add(new Meeting(5, 11,12));
meetings.add(new Meeting(6, 11,13));
meetings.add(new Meeting(7, 12,14));
schedule(meetings, 8, 14);
}
private static class Meeting {
int number;
int startTime;
int endTime;
public Meeting(int number, int startTime, int endTime) {
this.number = number;
this.startTime = startTime;
this.endTime = endTime;
}
@Override
public String toString() {
final StringBuffer sb = new StringBuffer("Meeting{");
sb.append("number=").append(number);
sb.append(", startTime=").append(startTime);
sb.append(", endTime=").append(endTime);
sb.append('}');
return sb.toString();
}
}
}
上面的思路3就是所谓的贪婪算法,也就贪心算法,是通过局部最优来推出全局最优,也就是说只考虑当前利益最大化。
你一定在想,贪心算法在解决会议调度问题的时候,是不是感觉很巧妙,想到了这个思路感觉很简单,可是最开始又是如何想到的呢?别着急,用贪心算法是有一定套路的
- 贪心算法通常用在求最值上面,比如最多,最大,最短等。示例就是求最大会议场次,因此以后看到求最值时,要想到有贪心算法这个东西。
- 贪心算法必定有一个贪心策略(也就是如何让后局部最优),贪心策略可能没那么容易一下就看得出来,但是贪心策略一定包含一个排序在里面。比如示例的思路1,2,3,对应3个贪心策略,其实就是3个排序。
- 贪心策略并不好选,因此你要做的事情通常是备选若干个策略,一个一个举例验证,最终挑选一个最合适的出来。
动态规划
动态规划算法,号称是最难理解的,本人也只是学点皮毛,供大家饭后消遣。
经典问题:背包问题
小偷去某商店盗窃,背有一个背包,容量是50kg,现在有以下物品(物品不能切分,且只有一个),请问小偷应该怎么拿才能得到最大的价值?
| 重量 | 价值 | |
|---|---|---|
| 物品1 | 10kg | 60元 |
| 物品2 | 20kg | 100元 |
| 物品3 | 40kg | 120元 |
咋一看,这个问题是求最值,好像可以使用贪心算法来求解,不信你可以试试各种贪心策略,总能找到反例(当然表格中的数据你的修改下)。
思路1,穷举法,每个物品都有两个状态,要么拿,要么不拿,可用二进制位来表示。那么3个物品可用3个位来表示,组合方式那么就有2^3个,000 001 010 100 011 101 110 111 。这种方式对于物品数量较小,比如小于10个的时候能够接受,在多几个物品,组合方式指数级增长,就算不出来了。
思路2,将背包可装的5kg,拆分成5个1kg的(为了方便推演,将原数据缩小10倍),来一个物品之后,在5个状态下分析当前价值最大化的情况。我们来画个表格来理解下这种思路。
-
物品1加入时,
当背包只有1kg时,能装下物品1,那么此时的最大价值为6元;
当背包有2kg时,能装下物品1,此时的最大价值还是为6元;
同理,背包有3kg、4kg、5kg时,最大价值都是6元。
| 物品\重量 | 1KG | 2KG | 3KG | 4KG | 5KG |
|---|---|---|---|---|---|
| 物品1(1KG,6元) | 6 | 6 | 6 | 6 | 6 |
-
当物品2加入时:
当背包只有1kg时,物品2装不下,因此当前单元格的最大价值为和只有物品1时一样,也就是继承上一个单元格的值,为6;
当背包有2kg时,物品2装得下,此时有两种选择,如果装物品2,刚好装满,价值为10元;如果不装,继承上一个单元格的价值为6,因此装物品2划得算,因此选择装,最大价值为10元;
当背包有3kg时,物品2装得下,此时有两种选择,如果装物品2,装之后还剩下1kg,因此价值为装物品2的10元+背包只有1kg时的最大价值6 = 16;如果不装,只有6,因此选择装。
当背包有4kg时,物品2装得下,此时有两种选择,如果装物品2,装之后还剩下2kg,因此价值为装物品2的10元+背包有2kg时的最大价值6(注意是除去物品2时的最大价值,因为只有一个物品,不能重复装) = 16;如果不装,只有6,因此选择装。
同理,背包有5kg时,最大价值为16元。
| 物品\重量 | 1KG | 2KG | 3KG | 4KG | 5KG |
|---|---|---|---|---|---|
| 物品1(1KG,6元) | 6 | 6 | 6 | 6 | 6 |
| 物品2(2KG,10元) | 6 | 10 | 16 | 16 | 16 |
-
当物品3加入时:
当背包只有1kg时,物品3装不下,因此当前单元格的最大价值为和有物品1和2时一样,也就是继承上一个单元格的值,为6;
当背包有2kg时,物品3装不下,因此当前单元格的最大价值为和有物品1和2时一样,也就是继承上一个单元格的值,为10;
当背包有3kg时,物品3装不下,因此当前单元格的最大价值为和有物品1和2时一样,也就是继承上一个单元格的值,为16;
当背包有4kg时,物品3装得下,此时有两种选择,如果装物品3,装之后还剩下0kg,因此价值为装物品3的12元;如果不装,继承上一个单元格的值,为16;因此选择不装。
当背包有5kg时,物品3装得下,此时有两种选择,如果装物品3,装之后还剩下1kg,因此价值为装物品3的12元+上一轮(没有物品3时)背包只有1kg时的最大价值6 = 18元;如果不装,继承上一个单元格的值,为16;因此选择装,最大价值18.
| 物品\重量 | 1KG | 2KG | 3KG | 4KG | 5KG |
|---|---|---|---|---|---|
| 物品1(1KG,6元) | 6 | 6 | 6 | 6 | 6 |
| 物品2(2KG,10元) | 6 | 10 | 16 | 16 | 16 |
| 物品3(4KG,12元) | 6 | 10 | 16 | 16 | 18 |
最后一个单元格就是能够得到的最大价值。
通过上面的推演,可以得出这样一个公式,当某个物品加入时,单元格最大价值的值 = max(装的价值, 不装的价值)。装的价值 = 当前装的物品的价值 + 剩余空间下上一轮(没有加入当前物品时)最大价值; 不装的价值就很好理解,相当于没有这个物品嘛,就等于上一轮最大价值。
现在,如果你觉得你理解了这个推导的过程,那么你可以思考下,最大价值时,是由哪些物品组成的呢?(后面的代码中有答案,但先不着急去看。)
明白了这个分析的过程,那么用代码实现出来也就没那么复杂了
/**
* 背包问题
*
* 背包可以装5kg,现有如下物品,问,如何装物品,才能价值最大化?
* 重量 价值
* item1 1kg 6
* item2 2kg 10
* item3 4kg 12
*
* 思路:
* 1. 粗暴的方式,可以通过排列组合方式,即每个物品都有两个状态,装或不装,如果用位来表示上面的这个问题
* 那么可能的组合方式有 000 001 011 010 011 100 101 111 一共2^3次方 = 8种组合。
* 这种解决方案称之为枚举,算法时间复杂度为O(2^n),当物品数量不多时,比如10以内 问题不大。
*
* 2. 动态规划
* 将背包可装的5kg,拆分成5个1kg的
* 来一个物品之后,在5个状态下分析当前价值最大化的情况。
* 比如来第一个物品时,它是1kg,价值是6,那么背包为1kg时,装的下,最大价值为 6. 背包为2kg时,最大价值还是6,一直到5kg,最大价值都是6.
* 来第二物品时,它是2kg,价值是10,
* 那么背包为1kg时,装不下,那么最大价值就是继承上上一轮中,背包为1kg时的最大价值,也就是6.
* 背包为2kg时,发现装得下,那么此时有需要看是装下时能够产生的价值最大,还是不装时,继承上一轮2kg时的价值最大。显然,装下物品2时,价值为10,大于上一轮中最大价值,当然选择装了
* 当背包为3kg是,发现装得下,同时还剩下1kg,那么1kg时,最大价值是6,因此本次的最大价值是10+6=16.
* 当背包为4kg时,最大价值16
* 当背包为5kg时,最大价值16
* 来第三个物品时,它是4kg,价值是12
* 那么背包为1kg时,装不下,那么最大价值就是继承上上一轮中,背包为1kg时的最大价值,也就是6.
* 背包为2kg时,装不下,那么最大价值就是继承上上一轮中,背包为2kg时的最大价值,也就是10.
* 背包为3kg时,装不下,那么最大价值就是继承上上一轮中,背包为3kg时的最大价值,也就是16.
* 背包为4kg时,装得下,那么此时有需要看是装下时能够产生的价值最大,还是不装时,继承上一轮4kg时的价值最大。
* 装下时产生的价值是12+0,而上一轮中,背包为4kg时的最大价值16,因此不装更划算
* 背包为5kg时,装得下,那么此时有需要看是装下时能够产生的价值最大,还是不装时,继承上一轮5kg时的价值最大。
* 装下时产生的价值是12+6,而上一轮中,背包为4kg时的最大价值16,因此装下的价值最高。
*
* 这样通过从上一个状态往下一个状态推算,这就是动态规划的思路,其最难的,也是最关键的就是 状态转移方程的推导。
*
*/
public class BagProblem {
public static void main(String[] args) {
Item item1 = new Item(1, 1, 6);
Item item2 = new Item(2, 2, 10);
Item item3 = new Item(3, 4, 12);
List<Item> items = new ArrayList<>();
items.add(item1);
items.add(item2);
items.add(item3);
items.forEach(System.out::println);
int weightCap = 5; //背包容量
int[][] value = new int[items.size() + 1][weightCap + 1]; //注意,+1是为了表格的表头加入进去,便于编码实现
for (int i = 1; i <= weightCap; i++) { //初始化行头,初始化为0,表示没有物品时的价值
value[0][i] = 0;
}
for (int i = 1; i <= items.size(); i++) { //初始化列头,初始化为0,表示没有容量时的价值
value[i][0] = 0;
}
//动态规划推导
for (int i = 1; i <= items.size(); i++) { //外层是物品
Item curItem = items.get(i - 1); //当前需要推导的物品
for (int j = 1; j <= weightCap; j++) { //内层来一个物品时,在不同的容量下,最大价值
int curBagCap = j; //当前推导中,背包的容量。
int maxValue;
if (curItem.weight > curBagCap) { //当前物品装不下,那么价值就是继承上一轮中,相同容量下的最大价值
maxValue = value[i - 1][curBagCap];
} else { //当前物品装得下,那么就要选择是装的时候的价值大,还是不装,继承上一轮中,相同容量下价值大
//装时的最大价值, 等于当前物品的价值 + 剩余重量下的最大价值(不能包含当前物品),
int valueOfHold = curItem.money + value[i-1][(curBagCap - curItem.weight)];
//不装时的最大价值,就是上一轮中相同容量下最大价值。
int valueOfNotHold = value[i - 1][curBagCap];
maxValue = Math.max(valueOfHold, valueOfNotHold);
}
value[i][j] = maxValue; //设置最大价值
}
}
//最大的容量下,所有物品都加入时的最大价值,就是是在最后一个格子里面。
System.out.println("能装的最大价值是:" + value[items.size()][weightCap]);
//物品组成
//思路,首先最后一个格子,从下往上两两比较,如果下面的大于上面的,表示这一行的物品选择了,
// 如果相等,则这一行的物品就没有选择。
// 如果选择了,那么下一次,就是在装了物品之后,剩下的重量的那一列进行比较了
int curWeightCap = weightCap; //当前的背包剩余重量
for (int i = items.size(); i >= 1 ; i--) { //从下往上遍历
if (value[i][curWeightCap] > value[i-1][curWeightCap]) { //当前物品选中
System.out.println("装下的物品:"+items.get(i-1));
curWeightCap = curWeightCap - items.get(i-1).weight ; //注意物品选择后,要减去占用的重量。
}
}
//把价值表格打印出来。
for (int i = 1; i <= items.size(); i++) {
for (int j = 1; j <= weightCap; j++) {
System.out.print(value[i][j] + "\t");
}
System.out.println();
}
}
private static class Item{
int id; //编号;
int weight; //重量
int money; //金额
public Item(int id, int weight, int money) {
this.id = id;
this.weight = weight;
this.money = money;
}
@Override
public String toString() {
final StringBuffer sb = new StringBuffer("Item{");
sb.append("id=").append(id);
sb.append(", weight=").append(weight);
sb.append(", money=").append(money);
sb.append('}');
return sb.toString();
}
}
}
其实解决背包问题,这整个推算的思路就是传说中的动态规划,通过把问题分成很多小阶段一段段的转移,从而得出最优解。背包问题的时间复杂度可以看到,O(m*n ), m为问题拆解粒度(这也是为什么推演表把数据量缩小10倍,背包问题就是重量拆解为5个1kg),n就是物品数量,算起来就是表格单元格个数。
动规难就难在这个推演过程,遇到类似问题的时候,只能慢慢的琢磨推演了。
用动规算法求字符串最长公共子串,你可以可视化看到推导过程:
最长公共子串:https://www.cs.usfca.edu/~galles/visualization/DPLCS.html