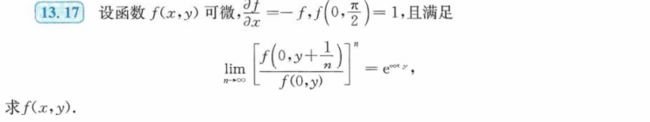高等数学张宇18讲 第十讲 多元函数微分学
目录
- 例题十
- 例10.3 设 z = f ( x , y ) = { ( x 2 + y 2 ) sin 1 x 2 + y 2 , x 2 + y 2 ≠ 0 , 0 , x 2 + y 2 = 0 , z=f(x,y)=\begin{cases}(x^2+y^2)\sin\cfrac{1}{\sqrt{x^2+y^2}},&x^2+y^2\ne0,\\0,&x^2+y^2=0,\end{cases} z=f(x,y)=⎩⎪⎨⎪⎧(x2+y2)sinx2+y21,0,x2+y2=0,x2+y2=0,则下列四个结论中,
(1) f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (0,0) (0,0)处连续;
(2) f x ′ ( 0 , 0 ) , f y ′ ( 0 , 0 ) f'_x(0,0),f'_y(0,0) fx′(0,0),fy′(0,0)存在;
(3) f x ′ ( x , y ) , f y ′ ( x , y ) f'_x(x,y),f'_y(x,y) fx′(x,y),fy′(x,y)在 ( 0 , 0 ) (0,0) (0,0)处连续;
(4) f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (0,0) (0,0)处可微。
正确的结论的个数为
( A ) 1 ; (A)1; (A)1;
( B ) 2 ; (B)2; (B)2;
( C ) 3 ; (C)3; (C)3;
( D ) 4. (D)4. (D)4. - 例10.16 求函数 f ( x , y ) = x 4 + y 4 − ( x + y ) 2 f(x,y)=x^4+y^4-(x+y)^2 f(x,y)=x4+y4−(x+y)2的极值。
- 例10.19 设 x , y x,y x,y为任意正数, n n n为正整数,求证 x n + y n 2 ⩾ ( x + y 2 ) n \cfrac{x^n+y^n}{2}\geqslant\left(\cfrac{x+y}{2}\right)^n 2xn+yn⩾(2x+y)n。
- 新版例题十三
- 例13.2
- 例13.4
- 例13.6
- 例13.8
- 例13.17
- 例13.18
- 新版习题十三
- 13.17
- 写在最后
例题十
例10.3 设 z = f ( x , y ) = { ( x 2 + y 2 ) sin 1 x 2 + y 2 , x 2 + y 2 ≠ 0 , 0 , x 2 + y 2 = 0 , z=f(x,y)=\begin{cases}(x^2+y^2)\sin\cfrac{1}{\sqrt{x^2+y^2}},&x^2+y^2\ne0,\\0,&x^2+y^2=0,\end{cases} z=f(x,y)=⎩⎪⎨⎪⎧(x2+y2)sinx2+y21,0,x2+y2=0,x2+y2=0,则下列四个结论中,
(1) f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (0,0) (0,0)处连续;
(2) f x ′ ( 0 , 0 ) , f y ′ ( 0 , 0 ) f'_x(0,0),f'_y(0,0) fx′(0,0),fy′(0,0)存在;
(3) f x ′ ( x , y ) , f y ′ ( x , y ) f'_x(x,y),f'_y(x,y) fx′(x,y),fy′(x,y)在 ( 0 , 0 ) (0,0) (0,0)处连续;
(4) f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (0,0) (0,0)处可微。
正确的结论的个数为
( A ) 1 ; (A)1; (A)1;
( B ) 2 ; (B)2; (B)2;
( C ) 3 ; (C)3; (C)3;
( D ) 4. (D)4. (D)4.
解 对于结论(3),当 ( x , y ) ≠ ( 0 , 0 ) (x,y)\ne(0,0) (x,y)=(0,0)时,用公式法求,
f x ′ ( x , y ) = 2 x sin 1 x 2 + y 2 + ( x 2 + y 2 ) cos 1 x 2 + y 2 ⋅ [ − 1 2 ⋅ 2 x ( x 2 + y 2 ) 3 ] = 2 x sin 1 x 2 + y 2 − x x 2 + y 2 cos 1 x 2 + y 2 . \begin{aligned} f'_x(x,y)&=2x\sin\cfrac{1}{\sqrt{x^2+y^2}}+(x^2+y^2)\cos\cfrac{1}{\sqrt{x^2+y^2}}\cdot\left[-\cfrac{1}{2}\cdot\cfrac{2x}{\sqrt{(x^2+y^2)^3}}\right]\\ &=2x\sin\cfrac{1}{\sqrt{x^2+y^2}}-\cfrac{x}{\sqrt{x^2+y^2}}\cos\cfrac{1}{\sqrt{x^2+y^2}}. \end{aligned} fx′(x,y)=2xsinx2+y21+(x2+y2)cosx2+y21⋅[−21⋅(x2+y2)32x]=2xsinx2+y21−x2+y2xcosx2+y21.
因为当 ( x , y ) ≠ ( 0 , 0 ) (x,y)\ne(0,0) (x,y)=(0,0)时, 2 x sin 1 x 2 + y 2 → 0 , x x 2 + y 2 cos 1 x 2 + y 2 2x\sin\cfrac{1}{\sqrt{x^2+y^2}}\to0,\cfrac{x}{\sqrt{x^2+y^2}}\cos\cfrac{1}{\sqrt{x^2+y^2}} 2xsinx2+y21→0,x2+y2xcosx2+y21不存在,故 lim ( x , y ) → 0 f x ′ ( x , y ) \lim\limits_{(x,y)\to0}f'_x(x,y) (x,y)→0limfx′(x,y)不存在,所以, f x ′ ( x , y ) f'_x(x,y) fx′(x,y)在 ( 0 , 0 ) (0,0) (0,0)处不连续。同理, f y ′ ( x , y ) f'_y(x,y) fy′(x,y)在 ( 0 , 0 ) (0,0) (0,0)处也不连续,所以结论(3)不成立。
对于结论(4),
Δ z = f ( 0 + Δ x , 0 + Δ y ) − f ( 0 , 0 ) = [ ( Δ x ) 2 + ( Δ y ) 2 ] ⋅ sin 1 ( Δ x ) 2 + ( Δ y ) 2 = ρ 2 sin 1 ρ , lim Δ x → 0 , Δ y → 0 Δ z − f x ′ ( 0 , 0 ) Δ x − f y ′ ( 0 , 0 ) Δ y ( Δ x ) 2 + ( Δ y ) 2 = lim ρ → 0 ρ 2 sin 1 ρ ρ = lim ρ → 0 ρ sin 1 ρ = 0 , \Delta z=f(0+\Delta x,0+\Delta y)-f(0,0)=[(\Delta x)^2+(\Delta y)^2]\cdot\sin\cfrac{1}{\sqrt{(\Delta x)^2+(\Delta y)^2}}=\rho^2\sin\cfrac{1}{\rho},\\ \lim\limits_{\Delta x\to0,\Delta y\to0}\cfrac{\Delta z-f'_x(0,0)\Delta x-f'_y(0,0)\Delta y}{(\Delta x)^2+(\Delta y)^2}=\lim\limits_{\rho\to0}\cfrac{\rho^2\sin\cfrac{1}{\rho}}{\rho}=\lim\limits_{\rho\to0}\rho\sin\cfrac{1}{\rho}=0, Δz=f(0+Δx,0+Δy)−f(0,0)=[(Δx)2+(Δy)2]⋅sin(Δx)2+(Δy)21=ρ2sinρ1,Δx→0,Δy→0lim(Δx)2+(Δy)2Δz−fx′(0,0)Δx−fy′(0,0)Δy=ρ→0limρρ2sinρ1=ρ→0limρsinρ1=0,
其中 ρ = ( Δ x ) 2 + ( Δ y ) 2 \rho=\sqrt{(\Delta x)^2+(\Delta y)^2} ρ=(Δx)2+(Δy)2。故 f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (0,0) (0,0)处可微,所以结论(4)成立。
故应选 ( C ) (C) (C)。(这道题主要利用了可微和偏导连续的判定求解)
例10.16 求函数 f ( x , y ) = x 4 + y 4 − ( x + y ) 2 f(x,y)=x^4+y^4-(x+y)^2 f(x,y)=x4+y4−(x+y)2的极值。
解
{ f x ′ = 4 x 2 − 2 ( x + y ) = 0 , f y ′ = 4 y 2 − 2 ( x + y ) = 0 ; ⇒ { x = − 1 , y = − 1 ; { x = 0 , y = 0 ; { x = 1 , y = 1 ; \begin{cases} f'_x=4x^2-2(x+y)=0,\\ f'_y=4y^2-2(x+y)=0; \end{cases}\Rightarrow\begin{cases}x=-1,\\y=-1;\end{cases}\begin{cases}x=0,\\y=0;\end{cases}\begin{cases}x=1,\\y=1;\end{cases} {fx′=4x2−2(x+y)=0,fy′=4y2−2(x+y)=0;⇒{x=−1,y=−1;{x=0,y=0;{x=1,y=1;
即得驻点 P 1 ( − 1 , − 1 ) , P 2 ( 0 , 0 ) , P 3 ( 1 , 1 ) P_1(-1,-1),P_2(0,0),P_3(1,1) P1(−1,−1),P2(0,0),P3(1,1)。又
A = f x x ′ ′ = 12 x 2 − 2 , B = f x y ′ ′ = − 2 , C = f y y ′ ′ = 12 y 2 − 2 ; A=f''_{xx}=12x^2-2,\quad B=f''_{xy}=-2,\quad C=f''_{yy}=12y^2-2; A=fxx′′=12x2−2,B=fxy′′=−2,C=fyy′′=12y2−2;
B 2 − A C ∣ P 1 = ( − 2 ) 2 − 10 ⋅ 10 = − 96 < 0 B^2-AC|_{P_1}=(-2)^2-10\cdot10=-96<0 B2−AC∣P1=(−2)2−10⋅10=−96<0,且 A ∣ P 1 > 0 A|_{P_1}>0 A∣P1>0,故 f ( − 1 , − 1 ) = − 2 f(-1,-1)=-2 f(−1,−1)=−2是极小值。
B 2 − A C ∣ P 2 = < 0 B^2-AC|_{P_2}=<0 B2−AC∣P2=<0,故 P 2 ( 0 , 0 ) P_2(0,0) P2(0,0)点的极值情况无法由二阶导数的充分性定理判别。由于 f ( x , y ) = x 4 + y 4 − ( x + y ) 2 f(x,y)=x^4+y^4-(x+y)^2 f(x,y)=x4+y4−(x+y)2,则在 ( 0 , 0 ) (0,0) (0,0)的任一邻域 x 2 + y 2 < δ 2 < 1 x^2+y^2<\delta^2<1 x2+y2<δ2<1内,取 ( ϵ , − ϵ ) (\epsilon,-\epsilon) (ϵ,−ϵ),得 f ( ϵ , − ϵ ) = 2 ϵ 4 > 0 f(\epsilon,-\epsilon)=2\epsilon^4>0 f(ϵ,−ϵ)=2ϵ4>0,而 f ( ϵ , ϵ ) = 2 ϵ 4 − 4 ϵ 2 = 2 ϵ 2 ( ϵ − 2 ) ( ϵ + 2 ) f(\epsilon,\epsilon)=2\epsilon^4-4\epsilon^2=2\epsilon^2(\epsilon-\sqrt{2})(\epsilon+\sqrt{2}) f(ϵ,ϵ)=2ϵ4−4ϵ2=2ϵ2(ϵ−2)(ϵ+2),由 0 < ϵ < 1 0<\epsilon<1 0<ϵ<1知,故 f ( 0 , 0 ) = 0 f(0,0)=0 f(0,0)=0不是极值。
B 2 − A C ∣ P 3 = − 96 < 0 B^2-AC|_{P_3}=-96<0 B2−AC∣P3=−96<0,且 A ∣ P 3 > 0 A|_{P_3}>0 A∣P3>0,故 f ( 1 , 1 ) = − 2 f(1,1)=-2 f(1,1)=−2也是极小值。(这道题主要利用了极值的充分性定理求解,具体的定理见下图)
例10.19 设 x , y x,y x,y为任意正数, n n n为正整数,求证 x n + y n 2 ⩾ ( x + y 2 ) n \cfrac{x^n+y^n}{2}\geqslant\left(\cfrac{x+y}{2}\right)^n 2xn+yn⩾(2x+y)n。
证 设 x + y = a x+y=a x+y=a,则原式化为在 x + y = a x+y=a x+y=a的条件下求 f ( x , y ) = x n + y n 2 ( 0 < x ⩽ a , 0 < y ⩽ a ) f(x,y)=\cfrac{x^n+y^n}{2}(0
新版例题十三
例13.2
例13.4
例13.6
例13.8
例13.17
例13.18
新版习题十三
13.17
写在最后
如果觉得文章不错就点个赞吧。另外,如果有不同的观点,欢迎留言或私信。
欢迎非商业转载,转载请注明出处。