简介
在之前的文章里,对于字符串的搜索算法,我曾经讨论过KMP算法的思路和实现。 KMP算法的实现思路是基于模式串里面的的前缀和后缀匹配,这种算法的效率已经足够快了。没想到的是,这里我们要讨论的Boyer Moore算法效率更加惊人。
思路分析
在之前的算法里,我们是通过从模式串的开头到结尾这么一个个的去和目标串比较,这种方式在碰到匹配的元素时则继续比较下一个,在没有匹配的时候,则通过查找模式表构建的匹配表来选择模式串里后面的第几个元素来继续进行比较。这样目标串里的索引就不用往回挪。但是,这里比较的顺序恰好相反。假设目标串长度为n, 模式串长度为m。那么,首先我们就从两个串的m - 1索引位置开始比较,如果相同,则一直向前,如果不同,则需要根据这个不同的字符的情况来判断。
根据比较字符的不同,我们可能有两种情况,一种是这个不同的字符不在模式串里。那么很显然,模式串里任何一个字符都不可能和它匹配的,我们只需要跳到这个字符的后面那个位置开始继续比较就可以了。还有一种情况就是这个字符是在模式串里的,那么,我们就需要找到和这个字符匹配的最后一个出现在模式串里的字符。这样,我们可以在模式串中从最后匹配的位置开始继续往后比较。
前面的这部分描述显得比较抽象,我们可以结合一个具体的示例来讨论。假设我们有字符串s和p,s的值为:FINDINAHAYSTACKNEEDLEINA, p的值为: NEEDLE。我们分别用i, j来表示s, p当前的位置。那么,他们比较的过程如下图:
结合上图来说,他们最开始比较的位置是从索引5开始。这个时候s在这个位置的元素是N,而p在这个位置的字符是E。那么他们并不匹配。我们就需要跳到后面进行比较。而这个字符N在p里面是存在的,对应p里最后出现N的位置就是索引0。所以我们就从N的这个位置开始到p最末尾的位置作为比较的点,又从p的末尾和对应的s的位置进行比较。这个时候i的索引位置为10的时候它和p最末尾的字符E并不匹配,而且这个字符是S,在p串里也找不到对应的字符。那么这时候,我们就需要从S后面的元素开始和p的第一个元素对齐,然后我们再从p的最后一个元素以及s串的索引i + j进行比较。这时候一直比较到开头,发现有匹配的串。于是返回i = 15。
概括
经过上述的讨论,我们发现,要实现这个算法需要考虑的就是怎么用一种比较简单的方法将字符串的匹配和不匹配场景给统一起来。这样在每次比较到匹配或者不匹配的时候能够对应的调整。对于前面的场景我们来仔细看一下。
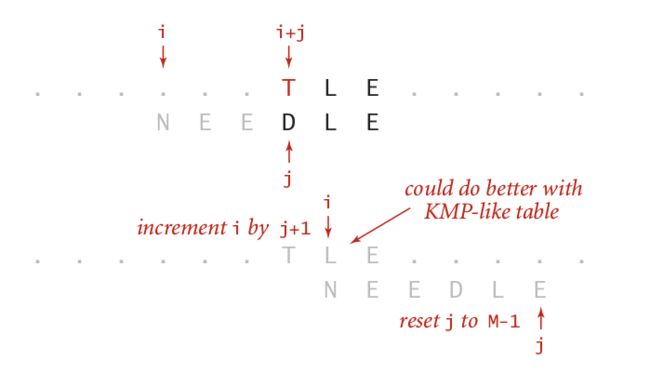
当比较的字符和当前p模式串里的字符不匹配时,如果这个不匹配的字符也不在模式串里,那么这种情形的调整如下图:
因为这种情况下,无论取模式串里的那个元素都不可能和这个元素匹配的,所以相当于要将整个模式串挪到这个元素的后面的那个位置对齐再来比较。这个时候,相当于将j重置到m - 1的值,而这个时候i的值也调整到i + j + 1 。
还有一种情况就是这个当前不匹配的字符在模式串里,如下图:
在这个示例里,因为不匹配的字符是N,但是N存在于模式串中。所以我们需要将i所在的位置移动到这个不匹配元素的位置。而这个时候模式串里的位置是j,如果我们可以找到N所在的索引位置,就可以通过j - right['N']来实现了。
所以总的来说,我们在比较的时候对于目标串的索引i和模式串的索引j来说,它们比较和调整顺序正好相反。i是逐步递增的调整,而j是递减的进行比较。当s.charAt(i + j) == p.charAt(j)的时候,表示它们匹配。所以这时候继续进行个j--这个操作进行下一步比较就可以。而s.charAt(i + j) != p.charAt(j)的时候,就要调整了。根据前面的讨论,如果s.charAt(i + j)不存在于p中间,这个时候,我们需要将i往右移动j + 1个位置。按照前面讨论的,也就是j - right[s.charAt(i + j)]。这也说明了right[s.charAt(i + j)] 为-1。
而如果s.charAt(i + j)存在于模式串中,那么我们需要找到这个字符在模式串中间的位置,我们需要移动的距离就是从j到这个字符的距离。如果用j - right[s.charAt(i + j)],那么这里right[s.charAt(i + j)]记录的应该就是字符s.charAt(i + j)在模式串中的位置。
这样,我们将right[]数组记录的值统一起来了。问题的核心就归结为怎么计算right数组。
计算right
计算right数组的过程比较简单,因为只要记录每个字符在模式串里最后出现的位置就可以了。对于不在模式串里的元素呢,只要设置为-1就可以了。所以我们可以用如下一段代码实现:
right = new int[r];
for(int c = 0; c < r; c++)
right[c] = -1;
for(int j = 0; j < m; j++)
right[pat.charAt(j)] = j;
最终实现
剩下的就是将整个实现给连贯起来。建立好right数组之后,剩下的就是从目标串i开始,每次比较s[i + j]和p[j]的位置。如果相等,就继续比较,直到j == 0。如果不等,则计算i后面要移动的距离skip,其中skip = j - right[s[i + j]]。这样,详细的实现如下:
public class BoyerMoore {
private int[] right;
private String pat;
public BoyerMoore(String pat) {
this.pat = pat;
int m = pat.length();
int r = 256;
right = new int[r];
for(int c = 0; c < r; c++)
right[c] = -1;
for(int j = 0; j < m; j++)
right[pat.charAt(j)] = j;
}
public int search(String txt) {
int n = txt.length();
int m = pat.length();
int skip;
for(int i = 0; i <= n - m; i+= skip) {
skip = 0;
for(int j = m - 1; j >= 0; j--) {
if(pat.charAt(j) != txt.charAt(i + j)) {
skip = j - right[txt.charAt(i + j)];
if(skip < 1) skip = 1;
break;
}
}
if(skip == 0) return i;
}
return -1;
}
}
在上述的代码实现里,还有一个值得注意的小细节,就是计算出skip之后,要判断skip是否小于1。因为有可能碰到的当前不匹配字符是存在于模式串里,但是它最后出现的位置要大于当前的值j了。这时候,我们要保证i最少要移动一位。所以这里要设置为1。
还有一个需要注意的地方就是,因为要考虑到为每个字符建立它的映射关系,所以我们需要建立一个有字符集长度那么长的right数组。在字符集太大的情况下,它占用的空间会比较多。这里只是针对理想的256个字符的情况建立的right表。
从该算法的性能来说,它在理想的情况下的时间复杂度为O(M/N) 其中M是目标串的长度,而N是模式串的长度。
总结
Boyer Moore算法是一个在实际中应用比较广泛的算法,它的速度更加快。和其他的字符串匹配方法比起来,它采用从后面往前的比较方式。同时通过建立一个字符映射表来保存字符在当前模式串里的位置,以方便每次比较的时候源串的位置调整。它最大的特点就是不再是一个个字符的移动,而是根据计算一次跳过若干个字符。这样总体的性能比较理想。
参考材料
http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/StringMatch/boyerMoore.htm
algorithms