卷积convolution函数详解及反向传播中的梯度求导
摘要
本文给出 convolution 函数的定义, 并求解其在反向传播中的梯度
相关
配套代码, 请参考文章 :
Python和PyTorch对比实现卷积convolution函数及反向传播
系列文章索引 :
https://blog.csdn.net/oBrightLamp/article/details/85067981
正文
1. 概念
灰度图片单通道卷积 :
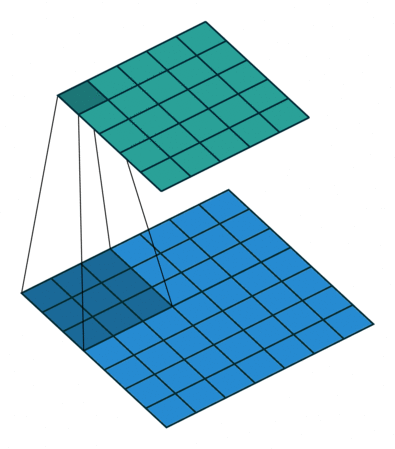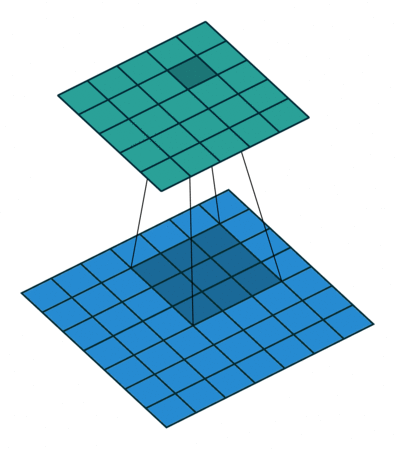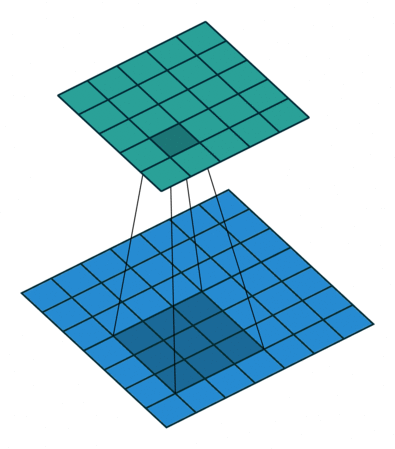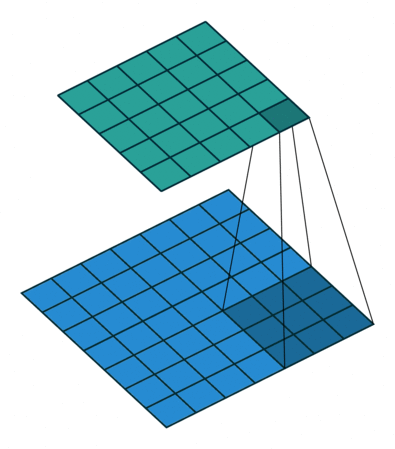
图片来源 : https://github.com/vdumoulin/conv_arithmetic
RGB图片三通道分别卷积, 将三个实数值结果相加 :
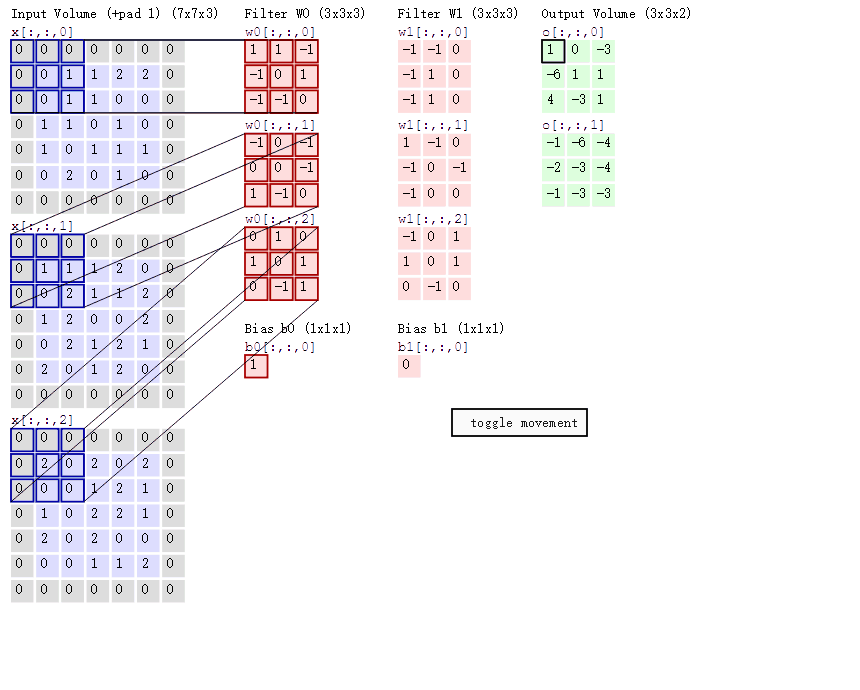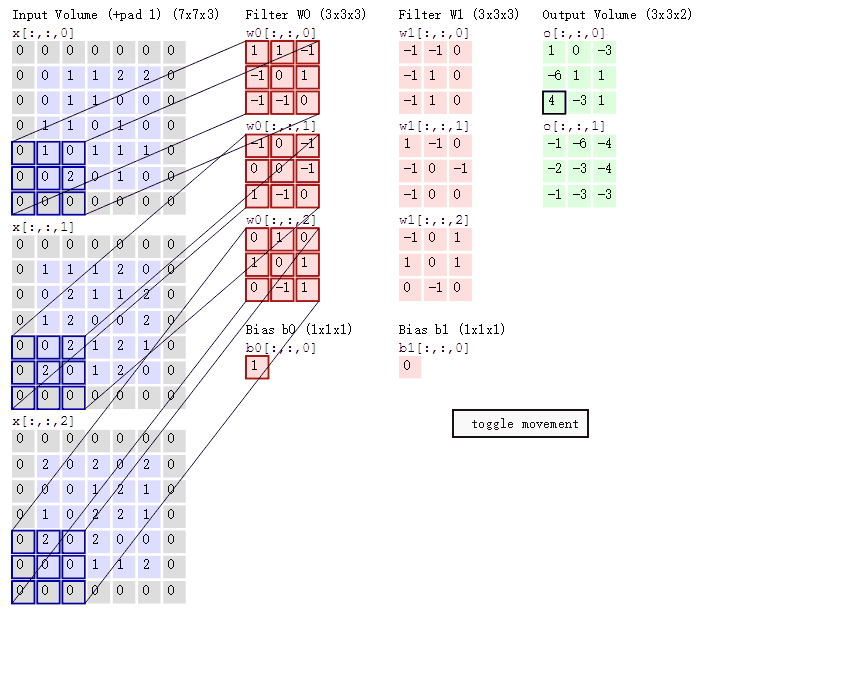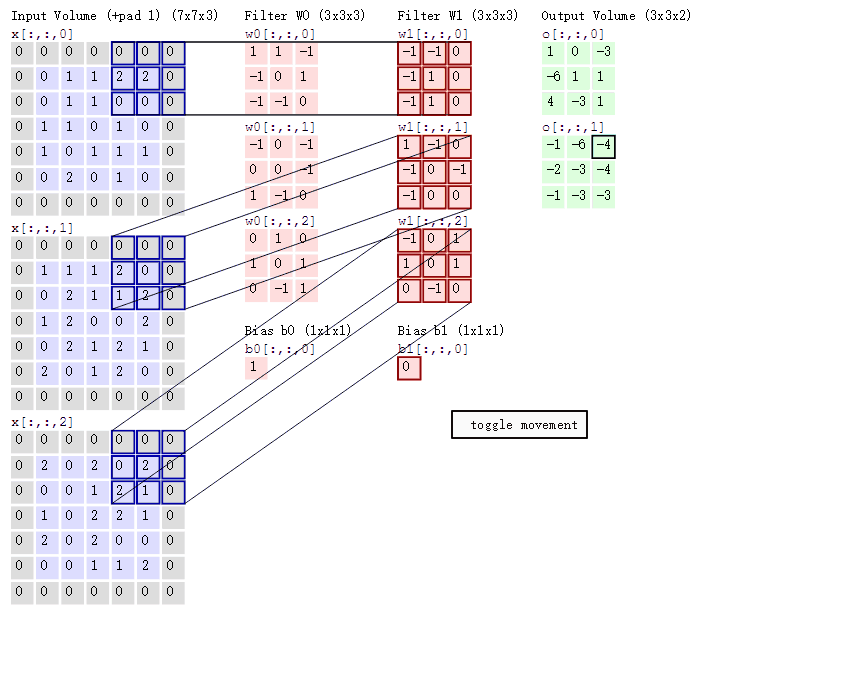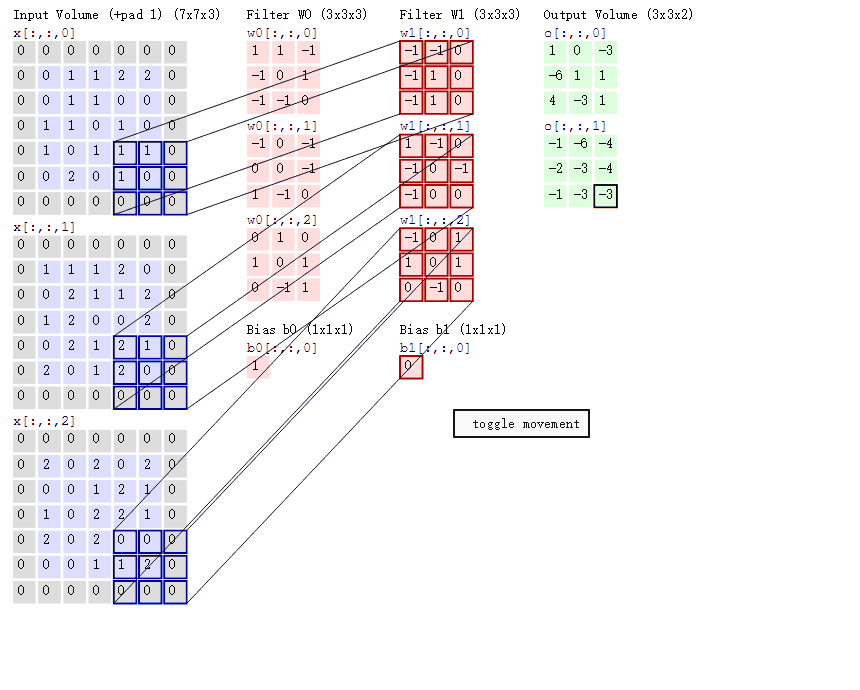
图片来源 : http://cs231n.github.io/convolutional-networks/
关于卷积的概念, 网络上已经有大量的详细资料, 都讲的很好, 这里就不再赘述了.
2. 卷积的定义
本文约定矩阵元素的脚标从 0 开始.
当 X 为 m x n 矩阵, W 为 2 x 2 矩阵, 步长为 1 时 :
y i j = ∑ i = 0 m − 2 ∑ j = 0 n − 2 ( x i , j w 00 + x i , j + 1 w 01 + x i + 1 , j w 10 + x i + 1 , j + 1 w 11 ) + b i ⩽ m − 2 j ⩽ n − 2 y_{ij} = \sum_{i=0}^{m-2}\sum_{j=0}^{n-2}(x_{i,j}w_{00} + x_{i,j+1}w_{01}+x_{i+1,j}w_{10} + x_{i+1,j+1}w_{11}) + b\\ \;\\ i\leqslant m-2 \\ \;\\ j\leqslant n-2 \\ yij=i=0∑m−2j=0∑n−2(xi,jw00+xi,j+1w01+xi+1,jw10+xi+1,j+1w11)+bi⩽m−2j⩽n−2
当 X 为 m x n 矩阵, W 为 p x q 矩阵, 步长为 1 时 :
y i j = ∑ r = 0 p − 1 ∑ s = 0 q − 1 x i + r , j + s w r s + b i ⩽ m − p j ⩽ n − q y_{ij} =\sum_{r=0}^{p-1}\sum_{s=0}^{q-1}x_{i+r,j+s}w_{rs}+ b\\ \;\\ i\leqslant m-p\\ \;\\ j\leqslant n-q\\ yij=r=0∑p−1s=0∑q−1xi+r,j+swrs+bi⩽m−pj⩽n−q
当 W 为 p x q 矩阵, 步长为 t, 为保证整除, 填充后的 X 是 m x n 矩阵时 :
y i j = ∑ r = 0 p − 1 ∑ s = 0 q − 1 x i ⋅ t + r , j ⋅ t + s w r s + b i ⩽ ( m − p ) / t j ⩽ ( n − q ) / t y_{ij} = \sum_{r=0}^{p-1}\sum_{s=0}^{q-1}x_{i\cdot t+r,j\cdot t+s}w_{rs}+b\\ \;\\ i\leqslant (m-p)/t\\ \;\\ j\leqslant (n-q)/t\\ yij=r=0∑p−1s=0∑q−1xi⋅t+r,j⋅t+swrs+bi⩽(m−p)/tj⩽(n−q)/t
偏置 b 为标量.
3. 反向传播
3.1 误差值对 X 的梯度的理论推导
当 W 为 p x q 矩阵, 步长为 t, 为保证整除, 填充后的 X 是 m x n 矩阵, 经 conv 卷积得到矩阵 g x h 矩阵 Y, 往前 forward 传播得到误差值 error (标量 e ). 上游的误差梯度向量 ∇ e ( Y ) \nabla e_{(Y)} ∇e(Y) 已在反向传播时得到, 求 e 对 X 的梯度.
已知 :
y i j = ∑ r = 0 p − 1 ∑ s = 0 q − 1 x i ⋅ t + r , j ⋅ t + s w r s + b i ⩽ ( m − p ) / t j ⩽ ( n − q ) / t y_{ij} = \sum_{r=0}^{p-1}\sum_{s=0}^{q-1}x_{i\cdot t+r,\;j\cdot t+s}w_{rs}+b\\ \;\\ i\leqslant (m-p)/t\\ \;\\ j\leqslant (n-q)/t\\ yij=r=0∑p−1s=0∑q−1xi⋅t+r,j⋅t+swrs+bi⩽(m−p)/tj⩽(n−q)/t
e = f o r w a r d ( Y ) ∇ e ( Y ) = d e d Y = ( ∂ e / ∂ y 11 ∂ e / ∂ y 12 ∂ e / ∂ y 13 ⋯ ∂ e / ∂ y 1 h ∂ e / ∂ y 21 ∂ e / ∂ y 22 ∂ e / ∂ y 23 ⋯ ∂ e / ∂ y 2 h ∂ e / ∂ y 31 ∂ e / ∂ y 32 ∂ e / ∂ y 33 ⋯ ∂ e / ∂ y 3 h ⋮ ⋮ ⋮ ⋱ ⋮ ∂ e / ∂ y g 1 ∂ e / ∂ y g 2 ∂ e / ∂ y g 3 ⋯ ∂ e / ∂ y g h ) e=forward(Y)\\ \;\\ \nabla e_{(Y)}=\frac{de}{dY}=\begin{pmatrix} \partial e/ \partial y_{11}&\partial e/ \partial y_{12}&\partial e/ \partial y_{13}&\cdots& \partial e/ \partial y_{1h}\\ \partial e/ \partial y_{21}&\partial e/ \partial y_{22}&\partial e/ \partial y_{23}&\cdots& \partial e/ \partial y_{2h}\\ \partial e/ \partial y_{31}&\partial e/ \partial y_{32}&\partial e/ \partial y_{33}&\cdots& \partial e/ \partial y_{3h}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ \partial e/ \partial y_{g1}&\partial e/ \partial y_{g2}&\partial e/ \partial y_{g3}&\cdots& \partial e/ \partial y_{gh}\\ \end{pmatrix} e=forward(Y)∇e(Y)=dYde=⎝⎜⎜⎜⎜⎜⎛∂e/∂y11∂e/∂y21∂e/∂y31⋮∂e/∂yg1∂e/∂y12∂e/∂y22∂e/∂y32⋮∂e/∂yg2∂e/∂y13∂e/∂y23∂e/∂y33⋮∂e/∂yg3⋯⋯⋯⋱⋯∂e/∂y1h∂e/∂y2h∂e/∂y3h⋮∂e/∂ygh⎠⎟⎟⎟⎟⎟⎞
求解过程 :
当 i ⋅ t + r = u , j ⋅ t + s = r 时 ∂ y i j ∂ x u v = { w u − i ⋅ t , v − j ⋅ t , i ⋅ t ⩽ u ⩽ i ⋅ t + p − 1 & j ⋅ t ⩽ v ⩽ j ⋅ t + q − 1 0 , o t h e r s , 其 他 情 况 当 \;\; i\cdot t+r =u,\;j\cdot t+s=r\;\;时\\ \;\\ \frac{\partial y_{ij}}{\partial x_{uv}}= \left\{ \begin{array}{rr} w_{u-i\cdot t,\;v-j\cdot t}\;\;, & i\cdot t \leqslant u \leqslant i\cdot t+p-1 \;\\ & \& \;\;j\cdot t\leqslant v \leqslant j\cdot t+q-1\\ 0\;\;, & others,\;其他情况 \end{array} \right. 当i⋅t+r=u,j⋅t+s=r时∂xuv∂yij=⎩⎨⎧wu−i⋅t,v−j⋅t,0,i⋅t⩽u⩽i⋅t+p−1&j⋅t⩽v⩽j⋅t+q−1others,其他情况
若卷积区出现重叠, 则:
i ( t + 1 ) ⩽ i ⋅ t + p − 1 o r j ( t + 1 ) ⩽ j ⋅ t + q − 1 i(t+1)\leqslant i\cdot t+p-1 \;\; or \;\; j(t+1)\leqslant j\cdot t+q-1 i(t+1)⩽i⋅t+p−1orj(t+1)⩽j⋅t+q−1
即 :
1 ⩽ t ⩽ p − 1 o r 1 ⩽ t ⩽ q − 1 1\leqslant t\leqslant p-1 \;\;or\;\; 1\leqslant t\leqslant q-1 1⩽t⩽p−1or1⩽t⩽q−1
由于 :
∂ e ∂ x u v = ∑ i = 0 g − 1 ∑ j = 0 h − 1 ∂ e ∂ y i j ∂ y i j ∂ x u v \frac{\partial e}{\partial x_{uv}} = \sum_{i=0}^{g-1}\sum_{j=0}^{h-1}\frac{\partial e}{\partial y_{ij}}\frac{\partial y_{ij}}{\partial x_{uv}} ∂xuv∂e=i=0∑g−1j=0∑h−1∂yij∂e∂xuv∂yij
删除零值项后得 :
1.当 u , v u,v u,v 满足:
i ⋅ t ⩽ u ⩽ i ⋅ t + p − 1 & j ⋅ t ⩽ v ⩽ j ⋅ t + q − 1 ( 条 件 1 ) i\cdot t \leqslant u \leqslant i\cdot t+p-1 \;\; \& \;\;j\cdot t\leqslant v \leqslant j\cdot t+q-1\;\;(条件1)\\ i⋅t⩽u⩽i⋅t+p−1&j⋅t⩽v⩽j⋅t+q−1(条件1)
∂ e ∂ x u v = { ( ∂ e / ∂ y i j ) w u − i ⋅ t , v − j ⋅ t , t ⩾ p , t ⩾ q ∑ x = 0 p − t ( ∂ e / ∂ y i − x ⋅ t , j ) w u − i ⋅ t , v − j ⋅ t , 1 ⩽ t ⩽ p − 1 , t ⩾ q ∑ y = 0 q − t ( ∂ e / ∂ y i , j − y ⋅ t ) w u − i ⋅ t , v − j ⋅ t , t ⩾ p , 1 ⩽ t ⩽ q − 1 ∑ x = 0 p − t ∑ y = 0 q − t ( ∂ e / ∂ y i − x ⋅ t , j − y ⋅ t ) w u − i ⋅ t , v − j ⋅ t , 1 ⩽ t ⩽ p − 1 , 1 ⩽ t ⩽ q − 1 \frac{\partial e}{\partial x_{uv}}= \left\{ \begin{array}{rr} (\partial e/\partial y_{ij}) w_{u-i\cdot t,\;v-j\cdot t}\;, & t\geqslant p,\; t\geqslant q\\ \sum_{x=0}^{p-t}(\partial e/\partial y_{i-x\cdot t\;,j}) w_{u-i\cdot t,\;v-j\cdot t}\;, & 1\leqslant t\leqslant p-1,\; t\geqslant q\\ \sum_{y=0}^{q-t}(\partial e/\partial y_{i,\;j-y\cdot t}) w_{u-i\cdot t,\;v-j\cdot t}\;, & t\geqslant p,\; 1\leqslant t\leqslant q-1\\ \sum_{x=0}^{p-t}\sum_{y=0}^{q-t}(\partial e/\partial y_{i-x\cdot t,\;j-y\cdot t}) w_{u-i\cdot t,\;v-j\cdot t}\;, & 1\leqslant t\leqslant p-1 ,\; 1\leqslant t\leqslant q-1\\ \end{array} \right. ∂xuv∂e=⎩⎪⎪⎨⎪⎪⎧(∂e/∂yij)wu−i⋅t,v−j⋅t,∑x=0p−t(∂e/∂yi−x⋅t,j)wu−i⋅t,v−j⋅t,∑y=0q−t(∂e/∂yi,j−y⋅t)wu−i⋅t,v−j⋅t,∑x=0p−t∑y=0q−t(∂e/∂yi−x⋅t,j−y⋅t)wu−i⋅t,v−j⋅t,t⩾p,t⩾q1⩽t⩽p−1,t⩾qt⩾p,1⩽t⩽q−11⩽t⩽p−1,1⩽t⩽q−1
其中, 上游误差梯度 ( ∂ e / ∂ y i j ) (\partial e/\partial y_{ij}) (∂e/∂yij) 已由上游计算给出. 这个式子从上到下分别为卷积区无重叠, 行重叠, 列重叠, 行列都重叠 4 种情况.
2.当 u , v u,v u,v 不满足上述条件1:
∂ e ∂ x u v = 0 \frac{\partial e}{\partial x_{uv}} = 0 ∂xuv∂e=0
3.2 编程方法
为方便编程实现, 定义一个操作 f f f :
f ( D , W , i , j ) : D [ i t : i t + p , j t : j t + q ] + = ( ∂ e / ∂ y i j ) W p × q \begin{array}{lr} f(D,W,i,j):\\ \;\;\;\;\;\;\;D[it:it+p,\;jt:jt+q]+\!=(\partial e/\partial y_{ij})W_{p \times q} \end{array} f(D,W,i,j):D[it:it+p,jt:jt+q]+=(∂e/∂yij)Wp×q
表示将 D 矩阵中, 从脚标为 i ⋅ t , j ⋅ t i \cdot t,\;\; j\cdot t i⋅t,j⋅t 的元素开始, 取和 W 形状相同的子矩阵, 并将该子矩阵的元素原位加上 W 矩阵乘以 ( ∂ e / ∂ y i j ) (\partial e/\partial y_{ij}) (∂e/∂yij) 后的元素. 参考的是 numpy 的记法.
将矩阵 D 按照矩阵 X 的形状使用零值初始化, 然后操作 f f f 按照 Y 的形状对所有的 i, j 遍历一遍. 最后矩阵 D 就是 e 对 X 的梯度矩阵, 和上面的数学公式是等价的.
3.3 误差值对 W 的梯度的理论推导
参考上例 :
y i j = ∑ r = 0 p − 1 ∑ s = 0 q − 1 x i ⋅ t + r , j ⋅ t + s w r s + b ∂ y i j ∂ w u v = x i ⋅ t + u , j ⋅ t + v ∂ e ∂ w u v = ∑ i = 0 g − 1 ∑ j = 0 h − 1 ∂ e ∂ y i j ∂ y i j ∂ w u v = ∑ i = 0 g − 1 ∑ j = 0 h − 1 ∂ e ∂ y i j x i ⋅ t + u , j ⋅ t + v y_{ij} = \sum_{r=0}^{p-1}\sum_{s=0}^{q-1}x_{i\cdot t+r,j\cdot t+s}w_{rs}+b\\ \;\\ \frac{\partial y_{ij}}{\partial w_{uv}}=x_{i\cdot t+u,j\cdot t+v}\\ \;\\ \frac{\partial e}{\partial w_{uv}} = \sum_{i=0}^{g-1}\sum_{j=0}^{h-1}\frac{\partial e}{\partial y_{ij}}\frac{\partial y_{ij}}{\partial w_{uv}}= \sum_{i=0}^{g-1}\sum_{j=0}^{h-1}\frac{\partial e}{\partial y_{ij}}x_{i\cdot t+u,j\cdot t+v}\\ yij=r=0∑p−1s=0∑q−1xi⋅t+r,j⋅t+swrs+b∂wuv∂yij=xi⋅t+u,j⋅t+v∂wuv∂e=i=0∑g−1j=0∑h−1∂yij∂e∂wuv∂yij=i=0∑g−1j=0∑h−1∂yij∂exi⋅t+u,j⋅t+v
结果简洁, 编程实现时可以直接使用.
3.4 误差值对 b 的梯度的理论推导
参考上例 :
∂ y i j ∂ b = 1 ∂ e ∂ b = ∑ i = 0 g − 1 ∑ j = 0 h − 1 ∂ e ∂ y i j ∂ y i j ∂ b = ∑ i = 0 g − 1 ∑ j = 0 h − 1 ∂ e ∂ y i j \frac{\partial y_{ij}}{\partial b}=1\\ \;\\ \frac{\partial e}{\partial b} = \sum_{i=0}^{g-1}\sum_{j=0}^{h-1}\frac{\partial e}{\partial y_{ij}}\frac{\partial y_{ij}}{\partial b}= \sum_{i=0}^{g-1}\sum_{j=0}^{h-1}\frac{\partial e}{\partial y_{ij}}\\ ∂b∂yij=1∂b∂e=i=0∑g−1j=0∑h−1∂yij∂e∂b∂yij=i=0∑g−1j=0∑h−1∂yij∂e
结果简洁, 编程实现时可以直接使用.
4. 补充说明.
4.1 多通道卷积
如果输入的数据包含多通道, 比如RGB彩色图片有红, 绿, 蓝三个通道相同尺寸的数据. 只要分别在这三个通道上进行卷积操作, 然后将结果加起来就可以了.
这三个卷积操作拥有独立的卷积核 W, 但偏置 b 是共享的, 一样的, 在最后的结果时才加上.
4.2 加快计算效率
为了避免两层循环嵌套, 可以将矩阵 X 和 W 都拉伸成一维向量, 加快计算效率. 但这样做会增加公式推导的复杂度, 这里就不展开讨论了.
4.3 PADDING 填充
在常见的深度学习框架算法中, 卷积操作都会集成 PADDING 填充操作.
本文默认输入的矩阵 X 已经做好了 PADDING 填充处理, 简化推导过程.
有兴趣的读者可以自行在卷积前添加一个维度整除判断及预处理操作, 而这并不会影响卷积部分的代码.
全文完