皇后游戏

题目背景

还记得 NOIP 2012 提高组 Day1 的国王游戏吗？时光飞逝，光阴荏苒，两年
过去了。国王游戏早已过时，如今已被皇后游戏取代，请你来解决类似于国王游
戏的另一个问题。

题目描述

皇后有 n 位大臣，每位大臣的左右手上面分别写上了一个正整数。恰逢国庆
节来临，皇后决定为 n 位大臣颁发奖金，其中第 i 位大臣所获得的奖金数目为第
i－1 位大臣所获得奖金数目与前 i 位大臣左手上的数的和的较大值再加上第 i 位
大臣右手上的数。
形式化地讲：我们设第 i 位大臣左手上的正整数为 ai，右手上的正整数为 bi，
则第 i 位大臣获得的奖金数目为 ci可以表达为：

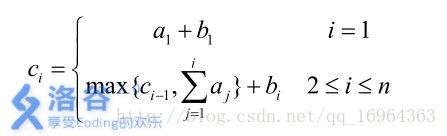
当然，吝啬的皇后并不希望太多的奖金被发给大臣，所以她想请你来重新安
排一下队伍的顺序，使得获得奖金最多的大臣，所获奖金数目尽可能的少。
注意：重新安排队伍并不意味着一定要打乱顺序，我们允许不改变任何一
位大臣的位置。

输入输出格式

输入格式：
第一行包含一个正整数 T，表示测试数据的组数。
接下来 T 个部分，每个部分的第一行包含一个正整数 n，表示大臣的数目。
每个部分接下来 n 行中，每行两个正整数，分别为 ai和 bi，含义如上文所述。

输出格式：
共 T 行，每行包含一个整数，表示获得奖金最多的大臣所获得的奖金数目。

输入输出样例

输入样例#1：
1
3
4 1
2 2
1 2
输出样例#1：
8
输入样例#2：
2
5
85 100
95 99
76 87
60 97
79 85
12
9 68
18 45
52 61
39 83
63 67
45 99
52 54
82 100
23 54
99 94
63 100
52 68
输出样例#2：
528
902

说明

按照 1、2、3 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 10；
按照 1、3、2 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 9；
按照 2、1、3 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 9；
按照 2、3、1 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 8；
按照 3、1、2 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 9；
按照 3、2、1 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 8。
当按照 3、2、1 这样排列队伍时，三位大臣左右手的数分别为：
(1, 2)、(2, 2)、(4, 1)
第 1 位大臣获得的奖金为 1 + 2 = 3；
第 2 位大臣获得的奖金为 max{3, 3} + 2 = 5；
第 3 为大臣获得的奖金为 max{5, 7} + 1 = 8。
对于全部测试数据满足： T≤10 T ≤ 10 , 1≤n≤20 000 1 ≤ n ≤ 20   000 , 1≤ai,bi≤109 1 ≤ a i , b i ≤ 10 9 。

【题解】
我们用对邻项微扰的方法解决，可以知道我们如果改变 i i 与 i+1 i + 1 将不会对其他人造成影响，同时我们知道右边的大臣总是大于左边的大臣所获得的奖赏，所以为了使获得奖赏最多的大臣所获得得最少，我们就要使得交换前比交换后的 i i 位更小
交换前：

ci=max{ci−1,∑j=1i−1aj+ai}+bi c i = m a x { c i − 1 , ∑ j = 1 i − 1 a j + a i } + b i

ci+1=max{max{ci−1,∑j=1i−1aj+ai}+bi,∑j=1i−1aj+ai+ai+1}+bi+1⋅⋅⋅⋅⋅⋅① c i + 1 = m a x { m a x { c i − 1 , ∑ j = 1 i − 1 a j + a i } + b i , ∑ j = 1 i − 1 a j + a i + a i + 1 } + b i + 1 · · · · · · ①

交换后:

ci=max{ci−1,∑j=1i−1aj+ai+1}+bi+1 c i = m a x { c i − 1 , ∑ j = 1 i − 1 a j + a i + 1 } + b i + 1

ci+1=max{max{ci−1,∑j=1i−1aj+ai+1}+bi+1,∑j=1i−1aj+ai+ai+1}+bi⋅⋅⋅⋅⋅⋅② c i + 1 = m a x { m a x { c i − 1 , ∑ j = 1 i − 1 a j + a i + 1 } + b i + 1 , ∑ j = 1 i − 1 a j + a i + a i + 1 } + b i · · · · · · ②

我们知道交换前与交换后的 ci总是<ci+1 c i 总 是 < c i + 1 所以我们考虑 ci+1 c i + 1
我们将①和②的式子略微化简得：
交换前：

ci+1=max{ci−1+bi+bi+1,∑j=1i−1aj+ai+bi+bi+1,∑j=1i−1aj+ai+ai+1+bi+1}⋅⋅⋅⋅⋅⋅③ c i + 1 = m a x { c i − 1 + b i + b i + 1 , ∑ j = 1 i − 1 a j + a i + b i + b i + 1 , ∑ j = 1 i − 1 a j + a i + a i + 1 + b i + 1 } · · · · · · ③

交换后：

ci+1=max{ci−1+bi+bi+1,∑j=1i−1aj+ai+1+bi+bi+1,∑j=1i−1aj+ai+ai+1+bi}⋅⋅⋅⋅⋅⋅④ c i + 1 = m a x { c i − 1 + b i + b i + 1 , ∑ j = 1 i − 1 a j + a i + 1 + b i + b i + 1 , ∑ j = 1 i − 1 a j + a i + a i + 1 + b i } · · · · · · ④

再一次发现两个式子的第一项相等，且剩下的每一项都有 ∑i−1j=1aj ∑ j = 1 i − 1 a j 所以删去，再一步化简得：
交换前：

ci+1=max{ai+bi+bi+1,ai+ai+1+bi+1}⋅⋅⋅⋅⋅⋅⑤ c i + 1 = m a x { a i + b i + b i + 1 , a i + a i + 1 + b i + 1 } · · · · · · ⑤

交换后：

ci+1=max{ai+1+bi+bi+1,ai+ai+1+bi}⋅⋅⋅⋅⋅⋅⑥ c i + 1 = m a x { a i + 1 + b i + b i + 1 , a i + a i + 1 + b i } · · · · · · ⑥

到此为止排序条件就出来了就是

max{ai+bi+bi+1,ai+ai+1+bi+1}<max{ai+1+bi+bi+1,ai+ai+1+bi} m a x { a i + b i + b i + 1 , a i + a i + 1 + b i + 1 } < m a x { a i + 1 + b i + b i + 1 , a i + a i + 1 + b i }

由于 1≤ai,bi≤109 1 ≤ a i , b i ≤ 10 9 我们开long long就可以解决了，但万一 ai,bi a i , b i 巨大，我们所以还得再化简
观察我们可以令每一项删去 ai+ai+1+bi+bi+1 a i + a i + 1 + b i + b i + 1 得：

max{−ai+1,−bi}<max{−ai,−bi+1} m a x { − a i + 1 , − b i } < m a x { − a i , − b i + 1 }

也就是

min{ai,bi+1}<min{ai+1,bi} m i n { a i , b i + 1 } < m i n { a i + 1 , b i }

#include
#include
#define LL long long
using namespace std;
struct Node {
    LL a,b;
} t[21000];
LL C[21000];
bool cmp(Node x,Node y) {
    return max(x.a+x.b+y.b,x.a+y.a+y.b)<
           max(y.a+x.b+y.b,x.a+y.a+x.b);
}
int main() {
    int T;
    scanf("%d",&T);
    while(T--) {
        int n;
        scanf("%d",&n);
        for(int i=1; i<=n; i++)
            scanf("%d%d",&t[i].a,&t[i].b);
        sort(t+1,t+1+n,cmp);
        LL sum=C[0]=0;
        for(int i=1; i<=n; i++) {
            sum+=t[i].a;
            C[i]=max(C[i-1],sum)+t[i].b;
        }
        printf("%lld\n",C[n]);
    }
    return 0;
}