此主要讨论图像处理与分析。虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来，但鉴于它们与计算机视觉的紧密联系，以 及它们的出处，没有把它们纳入到图像处理与分析中来。同样，这里面也有一些 也可以划归到计算机视觉中去。这都不重要，只要知道有这么个方法，能为自己 所用，或者从中得到灵感，这就够了。
8. Edge Detection
边缘检测也是图像处理中的一个基本任务。传统的边缘检测方法有基于梯度 算子，尤其是 Sobel 算子，以及经典的 Canny 边缘检测。到现在，Canny 边缘检 测及其思想仍在广泛使用。关于 Canny 算法的具体细节可以在 Sonka 的书以及 canny 自己的论文中找到，网上也可以搜到。最快最直接的方法就是看 OpenCV 的源代码，非常好懂。在边缘检测方面，Berkeley 的大牛 J Malik 和他的学生 在 2004 年的 PAMI 提出的方法效果非常好，当然也比较复杂。在复杂度要求不高 的情况下，还是值得一试的。MIT的Bill Freeman早期的代表作Steerable Filter 在边缘检测方面效果也非常好，并且便于实现。这里给出了几篇比较好的文献， 包括一篇最新的综述。边缘检测是图像处理和计算机视觉中任何方向都无法逃避 的一个问题，这方面研究多深都不为过。
[1980] theory of edge detection
[1983 Canny Thesis] find edge
[1986 PAMI] A Computational Approach to Edge Detection
[1990 PAMI] Scale-space and edge detection using anisotropic diffusion
[1991 PAMI] The design and use of steerable filters
[1995 PR] Multiresolution edge detection techniques
[1996 TIP] Optimal edge detection in two-dimensional images
[1998 PAMI] Local Scale Control for Edge Detection and Blur Estimation
[2003 PAMI] Statistical edge detection_ learning and evaluating edge cues
[2004 IEEE] Edge Detection Revisited
[2004 PAMI] Design of steerable filters for feature detection using canny-like criteria
[2004 PAMI] Learning to Detect Natural Image Boundaries Using Local Brightness, Color, and Texture Cues
[2011 IVC] Edge and line oriented contour detection State of the art
翻译
面向边缘和线条的轮廓检测：最新技术——http://tongtianta.site/paper/56281
作者：Giuseppe Papari *, Nicolai Petkov
摘要 -我们概述了过去二十年来提出的各种针对轮廓的边缘和线条定向方法。面向边缘和线的意思是不依赖于分割的方法。在边缘和轮廓之间进行区分。轮廓检测器分为本地和全局运算符。前者主要基于差异分析，统计方法，相位一致，等级排序过滤器及其组合。后者包括轮廓显着性的计算，感知分组，松弛标记和活动轮廓。涵盖了重要方面，例如旨在抑制纹理和噪声的预处理，多分辨率技术，计算模型与人类视觉系统的属性之间的联系，以及用于定量性能评估的过程和度量的使用。我们的主要结论是，考虑到多峰轮廓定义(通过亮度，颜色或纹理变化)，减少噪声和纹理的轮廓掩盖影响的机制，感知分组，多尺度方面和高水平，轮廓检测已达到高度复杂性水平视觉信息。
关键词：轮廓检测，预处理，局部模式分析，轮廓显着性，格式塔分组，闭合，比例空间，性能评估
目录
1.简介
2.预处理
2.1.本地自适应过滤
2.2.功能最小化和非线性扩散
2.3.讨论
3.局部模式分析
3.1.差分运算符
3.2.统计方法
3.3.相一致和局部能量
3.4.VOS和形态学边缘检测器
3.5.结合当地特色
3.6.讨论
4.上下文和全局方法
4.1.轮廓突出
4.2.根据格式塔原理将像素分组为轮廓.
4.3.活动轮廓
4.4.讨论
5.多分辨率方法
5.1.多分辨率分析
5.2.比例尺空间中的轮廓检测
6.绩效评估
6.1.一般方法
6.2.性能指标
7.1.线性局部方法的复杂性
7.2.非线性局部方法的复杂性
7.3.非本地方法的复杂性
8.总结，讨论和结论
8.1.取决于输入参数
8.2.计算步骤的相互依存
8.3.形状信息的重要性
1.简介
对象轮廓在人类视觉中起着重要作用。例如，临床证据表明，负责感知轮廓的大脑区域V1和V2受损，使患者完全无法识别物体[1]。图1显示了一个区域边界(通常是区域边界与对象轮廓重合)如何影响人类视觉感知的示例。在图像的两端，平均亮度是相同的。但是，由于中间的亮度不连续，图像的左部分显得比右部分更亮。这表明这种不连续性的存在不仅影响边界的直接邻域，而且还影响整个图像的感知。另一个示例如图2所示。两个对象图标在其95％的像素中相同，但是轮廓上的细微差异导致感知到两个对象在语义上完全不同。建立用于轮廓感知的计算模型的重要性超出了人类视觉系统的唯一理解。在计算机视觉的许多实际应用中，例如对象识别，机器人视觉或医学图像分析，都需要轮廓检测算法。
图1：人眼中边界的重要性：左图是通过在右图所示的1D亮度轮廓上添加合成纹理获得的。
图2.轮廓在形状识别中的重要性：尽管所示的心脏和苹果图标重叠了超过95％的像素，但由于轮廓不同，我们很容易将它们识别为不同的形状。
与计算机视觉中使用的其他概念类似，例如，他们不了解关于人脸识别的任何论文，其中给出了人脸概念的定义。几位作者倾向于将轮廓视为图像中有趣区域的边界。但是，这样的定义将排除轮廓不是由区域边界引起的重要情况。图3中给出了两个示例。对于左侧的合成示例，图像中的每条线都应视为轮廓，尽管这些线都不是不同颜色或纹理的两个区域之间的边界。换句话说，在此示例中，轮廓图与图像本身重合。在中间，我们有一个自然图像，并在此图像上有一个手工绘制的相关等高线图，均取自伯克利数据集[2]。如我们所见，同样在这种情况下，并非所有轮廓都来自区域边界，例如船的绳索。在图4中给出了另一个示例，其描绘了观察轮廓的四种不同方式。在前两幅图像中，轮廓由亮度和纹理的局部变化定义，而在第三种和第四种情况下，全局关系引起对轮廓的感知。如我们所见，仅在前两种情况下，轮廓是由区域边界产生的。我们宁愿假设需要在给定图像中绘制轮廓的人类观察者之间会有很大的集中度。 在[2]中提出的定量分析显示了这种一致性有多强，表明轮廓的概念被不同的观察者用来指代相同的特征。
图3：不是由区域边界产生的轮廓示例：(左)合成图像，其中轮廓图与图像重合；(中)来自伯克利数据集[2]的自然图像；(右) 相关的等高线图，它说明了等高线的概念比区域边界的概念更广泛(例如，参见船的绳索)。
图4：轮廓被感知的各种环境 从左到右：轮廓由亮度和纹理变化，感知分组或附近点以及虚轮廓线定义。
由于人类的判断是唯一可以用来判断给定视觉特征是否为轮廓的标准，因此我们在操作上将给定图像中的轮廓定义为人类观察者将集中的线集合作为轮廓在该图像中(可以对图像处理和视觉模式识别文献中使用的其他概念(例如人脸)进行类似的操作定义)。有鉴于此，轮廓检测的研究旨在以数学方式理解和建模人们(有意识地或有意识地)用来识别这些线集的特征(例如对比度，良好的连续性和闭合性)。
在本文中，我们提出了一种基于上述轮廓的运算定义的现有轮廓检测器算法的分类法。 具体来说，我们根据每种方法中使用的感知上重要的特征对轮廓检测算法进行分类。 这导致两类算法：(i)局部方法，其中定义的特征是亮度，颜色和纹理的局部差异；(ii)全局方法，其中基于良好的连续性和闭合性来识别轮廓。
由于各种实际原因，例如可能的低信噪比(SNR)或输入图像中存在纹理，轮廓检测是一项艰巨的任务。图5显示了一些图像示例，这些图像的轮廓无法通过简单的低级视觉模型检测到，并且还需要高级视觉提示(例如形状)的反馈。这意味着必须通过引入有关要检测轮廓的先验知识(例如形状)来解释输入图像。但是，这种低水平和高水平视觉提示的集成被证明是一项艰巨的任务，通常会导致非常复杂的模型和对计算要求很高的算法，这些算法仅在特殊情况下才有效。
图5：考虑到全球感知组织和对世界的了解，轮廓检测需要高水平视觉的解释和反馈的图像示例。
我们区分以下几类轮廓检测器：(i)面向区域的方法[3,4]，其中首先确定纹理或颜色恒定或缓慢变化的区域；然后将轮廓直接确定为封闭区域边界； (ii)面向边缘和线条的方法[5]，其中检测由亮度，颜色或纹理的对比度定义的线条或边界； (iii)混合方法[6]，其目的是区域和区域边界之间的一致性。在这里，我们对类(ii)的方法感兴趣。此类包括各种各样的技术，并且已针对每种特定方法类发布了概述文章。例如图像的微分结构分析[7](1994)，尺度空间理论[8,9](2001，2003)，统计分析，感知组织[10,11](1993，1999)和可变形模型，例如作为活动轮廓[12](1996)。 [6](1998)提出了边缘检测技术的一般概述。它主要侧重于局部方法，而上下文和全局技术(例如根据格式塔定律的边缘分组或活动轮廓)则没有深入讨论。旨在减少输入图像中的纹理和噪声以及进行定量性能评估的预处理也是尚未引起足够重视的问题。
我们承认有关基于区域的轮廓检测(即图像分割)方面的一些工作，在本次调查中不会对其进行深入处理。具体来说，最重要的技术是基于图论和割线[13,14]，迭代均值偏移[15]，统计方法[16,17]，分水岭[18,19]和多通道分析[20,21]。
在本文中，我们概述了轮廓检测的主要面向边缘和直线的方法，这些方法已在上述先前的调查报告中提出。在第二部分中，我们讨论了旨在改善轮廓检测结果的预处理技术。我们将在第3节中讨论基于差分和统计分析，相位一致性和形态梯度的局部边缘检测器。在第4节中，我们考虑上下文和全局轮廓检测器，它们基于轮廓显着性，边缘分组和活动轮廓的计算。由于本地和全局技术的输出都取决于分析图像的分辨率，因此我们也回顾了多分辨率轮廓检测器(第5节)。最后，我们在第6节中描述量化绩效评估程序，并在第8节中得出结论。
2.预处理
本节介绍了旨在简化连续轮廓检测的轮廓保持平滑器(图6)。与图像恢复算法不同，轮廓保留平滑器不仅要消除噪声，还要消除纹理，因为后者会干扰轮廓检测[22]。在第2.1节中讨论了局部轮廓保持平滑器，而在第2.2节中，我们考虑了基于变分方法和非线性扩散的全局轮廓保持平滑器。
2.1.本地自适应过滤
减少纹理和噪声的最著名技术是线性低通滤波。但是，由于边缘和拐角主要具有高频分量，因此这些功能也会衰减。为了克服这个问题，已经设计了几种局部非线性轮廓保持平滑器。一个称为自适应平滑的通用框架[24]包括计算局部加权，该局部加权包括计算每个像素r 的邻域N(r) 上灰度级的局部加权平均值，其中权重可以通过多种方式取决于局部模式配置。最著名的自适应平滑技术是双边滤波[25]，均值漂移[15]，值和标准滤波结构[26,27]以及秩次滤波(ROF)，也称为向量阶统计(VOS)[28]。
双边过滤。 在双边滤波中，权重由所谓的距离距离d = |I(p)-I(r)|的递减函数给出，权重是通过分析点r 和 ρ∈N(r)上的灰度值之间的局部密度分布得出的。 在均值平移中，均值平移的特殊情况[29]。 双向滤波和均值向量z = |p,I(p)|T均可以移动，这表明双向滤波具有良好的性能，尤其是在迭代使用的情况下。 然而，双边过滤受到术语 I(p)-I(r) 对噪声非常敏感这一事实的限制[23]。
值和标准过滤器结构。 不受此缺点影响的另一种方法是值和标准过滤器结构。 具体地，在N(r)的N个可能重叠的子区域上计算输入图像的N个加权局部平均值m和标准偏差s，i ＝ 1 ... N。 对于每个像素，运算符的输出由与具有最小si 的子区域相对应的mi 值给出。此类运算符的著名代表是Kuwahara和Gauss-Kuwahara滤波器[27]。 这种机制可以在保留边缘和角落的同时减少噪声和纹理，并且该框架包括几种作为特殊情况的现有滤镜[30]。 此类算子不适当，因为不清楚si 的最小值达到一个以上区域时，应选择mi 的哪个值。 在[23]中提出了一个适定的值和准则过滤器结构。
等级排序过滤器。 在ROF中，点pi∈N(r)，i = 1，…，N上的灰度是有序的，局部平均的权重取决于排序中的等级位置。 对于灰度图像，最常见的排序标准如下：
•从最暗到最亮的像素；
•根据数量|I(p)-I(r)|，ρ∈N(r)。
在第一种情况下，可以获得几种众所周知的过滤器，例如中值，加权中值，下中上层(LUM)过滤器[31]以及结构膨胀和侵蚀。 第二个准则引起k近邻去噪[32]。 对于诸如彩色图像之类的矢量值图像，可以制定不同的VOS排序标准[33，34]。 在[35]中介绍的最常见的是基于每个像素 ρk∈N(r)的总距离dk的计算，其中 l.I 是在有关颜色空间上定义的范数。
对于异常值较高，而对于所谓的向量中值则最低。 通常，ROF和VOS滤波器可以有效降低高斯噪声以及盐和胡椒噪声。
2.2.功能最小化和非线性扩散
一般概念。在本小节中，我们将讨论基于变分方法和偏微分方程的轮廓保持平滑器。我们仅涵盖问题的主要方面，请参考专业文献以进行更详尽的处理(例如，参见[36]及其参考文献)。可以通过搜索在支撑
上定义的函数U(r)来设计全局轮廓保持平滑器，该函数将形式为J = J1 + 入J2(其中
)的函数最小化，其中DnU是所有部分项的集合U的导数，直到n阶。对于平滑函数U(r)，项J1低，而J2是I(r)与U(r)之间的距离(常见选择是
)。系数 入 控制噪声抑制和数据拟合之间的权衡。 J 的最小值可以看作是观察到的信号 I 在给定功能空间中的投影，其中所有功能都具有某些所需的规律性。例子是函数有界变化的众所周知的空间，Sobolev空间以及最近推出的Meyer空间。我们参考[37]进行简要概述。
Tikohonov正则化。 已经详尽地研究了函数
[38，39]，并考虑了关于
的数学条件(有关的最常见选择的列表，请参见[39])。 重要的情况是
，称为二阶Tikohonov正则化[40，41]，以及
，称为总变异[42]。 Tikohonov正则化也称为线性正则化，因为可以通过线性滤波将相应的函数最小化，但是由于
的二次方，它对异常值不具有鲁棒性。 总变化对离群值更健壮，但仅对分段恒定图像最佳。 因此，当应用于平滑图像时，它可能会产生不希望的阶梯效果[43]。
Mumford-Shah实用。 总变化的一个众所周知的扩展是所谓的Mumford-Shah函数：分段恒定图像U(r)拟合到I(r)以及与恒定灰度级区域的轮廓的总长度有关的项 被添加到J [44]。 文献[36]提供了对总变异方法的调查，包括对Mumford-Shah函数的一些扩展。 其他扩展涉及矢量值图像[45、46]，在图形[46]上定义的图像，去模糊应用程序[47、48]以及将图像分解为三个分量(滤波图像，纹理和噪声)[37]。 图像处理中变分方法的数值方法和行为分析可以在[41,49]中找到。
通过非线性扩散使功能最小化。 最小化问题
可以通过将扩散方程
演化为稳态来解决，初始条件为u(r，t)= l(r)，其中F 是Euler- 拉格朗日导数(或一阶变式)[50]。 该观察结果将被认为彼此独立的图像处理的不同区域联系在一起。 在[51，52]中提出了通过最小化各种泛函推导的扩散方程的示例。 另一方面，不是所有形式为
的扩散方程，其中W是一般的非线性函数，都可以从变分问题中得出。 因此，非线性扩散的框架比功能最小化更为笼统。
非线性扩散已由[53]在图像处理中引入
形式的扩散方程的研究，其中g是一个正的非增量函数，并且已经详细研究了g的高斯和洛伦兹选择。 由于因数g(
)随着而减小，因此在高梯度幅度的点(例如边缘)处的扩散较低(图7)。 尽管已被广泛使用，但是该运算符有两个缺点：
)项。
的所有边，并模糊∥u∥
的所有边。因此，出于边缘检测的目的，它没有消除比简单的梯度阈值更多的纹理或噪声。
关于第一点，已经提出了上述扩散方程的几个正则化形式[54，55]。关于第二点，已经提出了许多不同的扩散方程[50,56,57]。其中许多是由于等渗线 u(r, s)=常数(随着s的增加)的运动而产生的。特别是，已经非常关注扩散方程，其中W(u)仅取决于等渗线的局部曲率[50]。非线性扩散框架的其他扩展涉及冲击滤波器[58]，矢量值图像[59,60]以及基于小波的扩散方程的解[61]。非线性扩散和局部轮廓保持平滑器之间的联系，例如自适应平滑，双边滤波和均值偏移，在[29]中以及其中的参考文献中进行了显示。
图7.从左到右：合成输入图像以及线性和非线性扩散的结果。
该框架还提供了可能自然地组合适用于不同补充任务的图像处理方案的可能性：例如，如果M算子以扩散方程的形式
表示，则可以从扩散方程
获得新的算子，
。 一个例子是高斯模糊形态学锐化的组合，这导致了高斯-夸瓦哈拉滤波器的PDE公式[27]。
2.3.讨论
总而言之，旨在减少纹理和噪声同时保留或增强对象轮廓的预处理是轮廓检测的重要方面。经典的局部自适应平滑技术，例如双边过滤，均值漂移和值以及标准过滤器结构在存在自然纹理和高斯噪声的情况下具有良好的性能，而VOS过滤器更适合于去除盐和胡椒噪声。前面提到的大多数非线性滤波器都可以合并到PDEs的框架中。它还提供了自然组合可用于不同补充任务的图像处理方案的可能性。 PDEs 的公式非常通用，因为在特殊情况下，它包含几个局部轮廓保持平滑器，以及基于功能最小化的运算符。 PDE方法的主要局限性在于该方法的迭代性质以及需要通常由启发式方法定义的迭代停止规则的计算复杂性。
3.局部模式分析
3.1.差分运算符
连续公式：输入亮度曲线的不连续性可以检测为高梯度幅度的点。因此，人们对图像的差分结构投入了很多兴趣。在本节中，我们使用量规坐标u和v [62]，定义它们的目的是使线u = constant和v = constant分别正交于并平行于局部梯度方向。在这些坐标中，梯度量仅是一阶导数
，边被标识为lv在v方向上的局部最大值，因此它们满足条件lv v = 0和lv v v <0。 lvv通常由拉普拉斯
= luu + lv v [63，64]代替，它是线性的，计算量较小，并且lv v近似良好(特别是，两个算子在零曲率点重合，对于luu = 0 )。在[65]中可以找到lv v和的边缘检测精度的定量比较。基于输入图像及其拉普拉斯算子的线性组合的生物驱动方法已证明比单独的拉普拉斯算子具有更好的边缘精度[66，67]。不满足条件lv v v <0的lv v(或拉普拉斯算子)的零交叉是梯度幅度的局部最小值，并且不对应于真实边缘。它们在文献中被称为幻影边缘，并已进行了详尽的研究[68]。
正规化区分离散支持上定义的函数的不适定问题的另一种方法是用拟合函数f(x，y)拟合每个像素周围的局部图案，并分析计算f(x，y)的导数[77,78]。最著名的拟合函数是多项式，其系数通过最小化均方误差来获得。在这种情况下，可以通过线性过滤来计算系数，并且将给定点的f(x，y)的导数表示为这些系数的线性组合[79,80]。在[81]中，表明局部函数拟合与可用函数有关。在[81]中利用这一事实进行有效的边缘检测，并在[82]中提出了基于Zernike矩的模型。在[83]中，三次样条模型用于检测屋顶边缘，在[84,85]中，提出了基于正则三次样条模型的比例空间。如果拟合函数f(x，y)不是多项式，或者拟合标准不是均方误差的最小值，则该过程不再是线性的。在[86]中可以找到对线性和非线性拟合模型的最新研究，并将其应用于边缘检测。
微分方法最重要的局限性在于，它们不区分一方面的纹理边缘与另一方面的区域边界和对象轮廓。最后，我们注意到Canny方法[73]是迄今为止最受欢迎的微分算子，它几乎已成为边缘检测的代名词。
3.2.统计方法
将N(r)分为两个相等的部分
，并使用独立性的两个样本统计检验来测量两个半部分之间的不相似性。 高的相异性值表明存在区域边界。 对多个方向重复进行此分析，并将引起最大差异的方向视为局部轮廓方向。 为此，已经部署了一些两个样本的统计检验，例如 χ
2 [87]，似然比[88]，Wilkoxon [89]，T [89]和Kolmogorov-Smirnov检验[89]。
这些检测纹理过渡的方法的有效性如图9所示。在[90]中，这些思想已经扩展到彩色图像：两个半邻区的颜色分布是通过矢量量化算法根据紧凑的颜色特征来描述的。色标之间的地球移动距离[91]用于检测轮廓的存在(图10)。最近，在[2,92,93]中，此方法已扩展到纹理。这些方法具有良好的性能，但是对计算的要求很高，因为必须对每个点的多个方向重复进行统计分析。此外，在存在高曲率轮廓点或比N(r)窄的细长物体(例如，浅色，金属丝，细血管等)的情况下，半圆形是不合适的。
其他统计方法着眼于通过分析梯度的协方差矩阵Q来检测梯度轮廓的分布。局部轮廓强度和局部轮廓取向是从Q的特征值和特征向量得出的(图11)。其他算法[96,97]仅使用N(r)内部的梯度方向，轮廓的存在以低角度分散为特征。这些差分统计方法能够检测轮廓和线条。它们的特征在于两个比例尺参数：N(r)的大小和用于估计梯度的邻域半径。对于轮廓检测应用，两个比例尺参数应近似相等。但是，如果前者比后者大得多，则可以将这些方法用于方向纹理的统计分析[95]。部署用于轮廓检测的其他局部统计数据基于共现矩阵[98]和其颜色与中央像素的颜色足够相似的像素部分[99]。
总而言之，基于局部统计分析的算法比差分方法更有效：实际上，它们检测由颜色和纹理过渡确定的边缘，但同时，对计算的要求更高。
3.3.相一致和局部能量
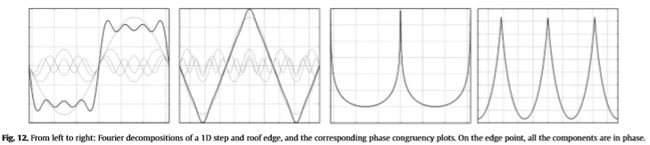
相位一致。 Oppenheim和Lim [100]的实验证明了相位在人类感知图像中的重要性。 进一步的心理证据[101,102]指出，人类视觉系统对自然图像中相位信息高度有序的点有强烈的反应。 通过引入一维信号x(t)的相位一致，在[103]中提出了这种现象的计算模型，定义为
是x(t)的傅立叶变换的幅度和相位。 在所有傅立叶分量同相的点上，该数量始终在0和1之间，为1(图12)。 对于2D信号，可以通过考虑图像的1D投影来计算不同方向的相位一致性。 可以看出，这些点对应于明显的视觉事件，例如台阶，峰顶和屋顶边缘[104]。 因此，可以通过分析相位一致性来执行边缘提取。
图12：从左到右：一维台阶和屋顶边缘的傅立叶分解，以及相应的相全图。 在边缘点，所有组件都同相。
当地能源。在[103]中，显示了PC(t)的局部最大值对应于分析信号x(t)= x(t)+ i xH(t)的大小的局部最大值，其中xH(t)是希尔伯特变换x(t)的xH(t)的计算涉及整个频谱，而许多计算机视觉应用程序都需要空间和频率定位。因此，将x(t)和xH(t)替换为它们的带通版本。因此，代替解析信号，计算称为局部能量的量
，其中fe(t)和fo(t)是对称函数和反对称函数，从而fo(t)是希尔伯特变换fe(t)的已经研究了几对函数fe(t)和fo(t)，这些函数产生了文献中称为正交对滤波器的滤波器，例如Gabor，Log-Gabor，Gaussian导数，Gaussians差和Cauchy功能[105]。其他例子是鲁棒的正交滤波器[106]和在坎尼准则[75]的意义上的最佳滤波器。这些过滤器的最新比较研究已在[105]中提出。最著名的正交滤波器是Gabor能量滤波器，它在空间和频率不确定性之间提供了最佳折衷方案[107]。可以在[108]中找到对其特性和应用的最新调查。
从1D到2D。将这些滤波器扩展到多维情况并不容易，因为不可能找到各向同性和反对称的标量函数。解决这个问题的最常见方法是针对不同方向实现各向异性正交滤波器，然后将输出与某种算法结合起来(有关简要概述，请参见[105])。但是，这些方法通常基于试探法，并且线性度丢失。最近，在[109]中提出了一种优雅的分析信号泛化，称为单基因信号，其基础是矢量函数既可以是各向同性的又可以是反对称的。
应用。 文献中已经提出了几种基于局部能量和相位一致性的边缘检测器和特征提取算法。 在[104]中，提出了基于小波的相位一致性实现。 在[110]中表明，与线性过滤不同，局部能量分析不仅可以识别台阶边缘，还可以识别屋顶边缘和峰顶边缘。 在[111]中，引入了约束相位一致性的概念，显示了其检测边缘和其他显着特征(例如马赫带)的能力。 在[112,113]中，局部能量模型用于检测较大的一组边缘特征，包括结和线端接。 如[114]中讨论的那样，检测屋顶，线和马赫带边缘的局部能量模型的能力使该算子成为幂等。 换句话说，给定输入图像I，基于局部能量的边缘检测器
满足条件
。 其他发展可以在[115,116]中找到。
总之，局部能量和相位一致性方法的成功主要是由于(i)考虑了图像中相位的感知重要性，以及(ii)它们检测不同类型的边缘(例如台阶)的能力，坡道，屋顶和线，从而形成一个统一的框架。此外，基于相位一致性的边缘检测器满足幂等条件[114]。然而，对于实际应用，局部能量方法的执行与更快且概念上更简单的差分方法[2]相似。
3.4.VOS和形态学边缘检测器
VOS过滤器的一般框架已在第2.1节中介绍。 在本节中，我们表明，使用适当的局部线性组合系数，这些滤波器会对输入亮度或颜色配置文件的不连续性做出反应。 最简单的例子是形态梯度[117,118]，定义为I 在N(r)上的最大值和最小值之间的差，或者等效地，是膨胀和腐蚀结果之间的差：
，可以重写 作为
。 通过将绝对值替换为色彩空间中的适当范数，可以将最后一个方程式直接扩展到彩色图像(色彩形态梯度[119])。 这种方法是快速的，但是对于离群值却不可靠。 为了使它对异常值更加稳健，在[119]中，| I(p)-I(r)I的最高值被排除在最大值的计算之外。
在[120]中已经提出了一些具有更多非零系数的更复杂的滤波器。 这些滤波器对高斯噪声，盐和胡椒噪声均具有鲁棒性，但以更高的计算复杂度为代价。 这些和其他颜色边缘检测器的性能比较在[121]中进行了介绍。
一方面，这些算法与微分算子和上述基于线性过滤的其他算法有一些相似之处，因为它们计算邻域中N(r)的值的线性组合。不同之处在于，系数与等级相关，而不与空间位置相关。另一方面，它们通过计算值等级类似于本地统计分析。通常，VOS边缘检测器的计算成本低于统计方法。VOS处理矢量图像的自然方式导致其主要应用于彩色图像[120]。
3.5.结合当地特色
在前面的小节中，考虑了边缘检测问题的互补方面，考虑了不同的局部特征。为了将由不同的本地特征执行的信息组合在一起，已经做了相当大的努力。这个想法是利用可用的基本事实中包含的语义信息来训练在相关特征空间中工作的分类器。分类器返回一个我们称为边缘似然度L的量(例如后验概率或Fisher判别式[122])。阈值L等效于在相关特征空间中对具有最佳决策边界的边缘像素进行分类。
在[123]中，输入图像的每个像素都与一个二维特征向量关联，该特征向量的分量是通过梯度幅度和线性非位移不变模板匹配分析获得的。但是，决策边界不是从一般原则得出的。在[124]中，采用贝叶斯方法来衡量通过组合以下局部特征而带来的性能改进：梯度幅度，局部能量分析的输出[110]和尼兹伯格边缘强度[94]。在[2]中进行了更详尽的研究，其中考虑了更大的局部特征集，包括颜色和纹理梯度。在[2,125]中研究了边缘检测性能对分类器选择的依赖性。
3.6.讨论
本节中所讨论的大多数局部边缘特征都是基于线性滤波的，即基于围绕每个点r 的局部图案P(r)与固定模板T的内积。模板的设计方式是使输出预期在几种类型的边缘上较高，而在平坦或均匀纹理区域上较低。然而，通过简单地将P(r)乘以适当的因子，可以使〈T，P(r)〉为任意高或低。因此，无论使用哪种模板T，足够高的对比度噪声将始终比低对比度边缘产生更高的响应。由于这些问题，一些作者建议针对其他局部量(例如P(r)的方差或其他相关量)对内积进行归一化。但是，这些新功能还有其他一些局限性——例如，它们往往在对比度非常低的区域反应过度。为了解决这些问题，在3.2节中提出了多种用于边缘检测的非线性算子。但是，由于一些限制-例如高计算复杂度，较差的性能或在线性情况下必须采用类似的限制，因此非常直接地导致了简单的最佳解决方案。
上述局部方法的一个更严重的局限性是，仅基于每个点的小邻域来确定像素是否属于轮廓。另一方面，容易产生图像，其中在视觉上类似于边缘的局部图案不属于对象轮廓，反之亦然(参见例如图5)。这一事实促使许多作者开发出更复杂的方案，其中也考虑了全球信息，下一部分将对此进行回顾。
4.上下文和全局方法
为了在轮廓检测中使用上下文信息和全局信息，已经做出了相当大的努力。 这些方法可以分为三类：所谓的轮廓显着性的计算(第4.1节)，轮廓中的像素分组(第4.2节)和活动轮廓(第4.3节)。
4.1.轮廓突出
各种心理生理学和神经生理学研究(例如参见[126,127]及其参考文献)表明，周围环境中存在其他类似的刺激会影响人类视觉系统对定向刺激的反应。已经确定了两种机制：
•刺激与中心刺激共线；
•周围抑制或其他刺激的抑制。
这些发现启发了几位作者分两步进行轮廓检测(图13)：首先，计算了局部边缘强度L(r)(例如，作为梯度幅度或Gabor滤波器的响应)。其次，取决于周围环境，L(r)被禁止或增强。结果是信息量更大的G(r)，即轮廓显着性。
图13：两步轮廓检测。 局部上下文分析通过增强轮廓并减少纹理和噪声来提高对象轮廓的可见性。
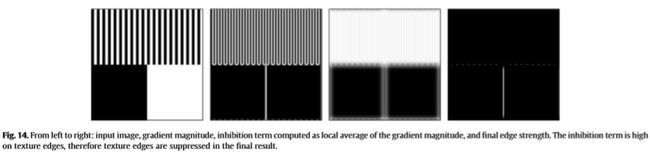
环绕声抑制。 [22,128]中提出了一种简单的环绕声抑制模型。它基于抑制项T(r)的计算，该术语被定义为每个像素周围的环上L(r)的局部平均值。T在孤立的边缘上较低，在纹理上较高，因此从边缘强度中减去T会导致对纹理边缘的响应降低，因此提高了对象轮廓和区域边界的可见性，如图14所示。这种方法已经以几种方式得到了进一步发展：在[129]中，环形抑制邻域沿着局部边缘方向分为两半，以消除轮廓的不希望的自抑制并减少沿区域边界的抑制。该模型也已集成在多分辨率框架中[130,131]，并与多阈值方法[132]结合在一起。可以将环绕声抑制作为后处理步骤应用于第3节中讨论的任何本地运算符的结果。到目前为止，它已被应用于微分(Canny)和局部能量(Gabor)方法。环绕抑制的主要优点是消除纹理边缘，应将其用于存在此类边缘问题的应用中。
图14：从左到右：输入图像，梯度幅度，以梯度幅度的局部平均值计算的抑制项以及最终边缘强度。 抑制项在纹理边缘较高，因此最终结果将抑制纹理边缘。
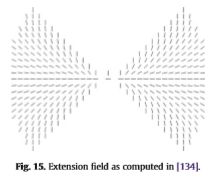
便利。 关于简化，计算轮廓显着性的最著名方法之一是张量投票[133]。 向量场Ex(r)，称为扩展场，与图像的每个像素x相关联(图15)。 考虑到在r和x处的边沿方向，矢量Ex(r)沿曲线的方向在良好连续性方面最可能连接点r和x。 E的大小就是这种可能性的值，通常它是 r-x 和弧度(r，x)的递减函数。 以此方式，图像的每个像素的特征在于图像中所有其他像素的值分布(所谓的票数)，并且从该分布的统计信息中获得了显着性图。 在[134]中，考虑了协方差矩阵K，并且从K 的特征值和特征向量获得了显着性值和局部边缘方向。例如，在[135]中可以找到该技术的进一步发展。
图15：在[134]中计算的扩展字段。
最近的工作[136,137]显示，类似于张量投票的方案可以成功地对在人类视觉系统的前端部分执行的简化和轮廓整合过程建模。大脑的这一部分被建模为3D神经元网格，对定向刺激做出反应。神经元在网格中位置的前两个坐标与边缘的空间位置有关，第三个坐标与边缘的方向有关。几个心理物理实验表明，可以通过张量投票之类的方法来模拟同时引起抑制和促进现象的神经相互作用。为了考虑抑制和促进作用，定义了特殊的扩展场，在心理物理学文献中被称为关联场[138]。有关相关生物学背景的概述，请参见[139,140]。在[141,142]中提出了基于抑制和促进的其他近期方法。
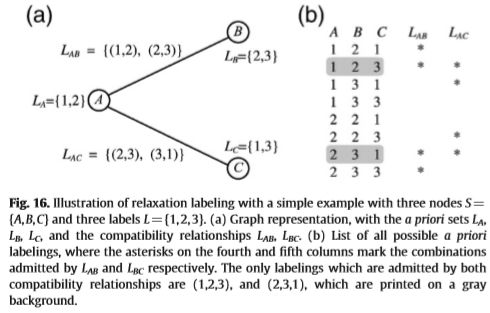
放宽标签。 一个用于计算显着性的强大的基于概率图的框架是松弛标记，它在[143]中引入，并在[144,145]中相继开发，并应用于轮廓检测。 用其最简单的表示法，可以引入松弛标记，如下所示：令S = {s1，…，sN}为图G的一组节点，而L = {l1，…，lm}为一组标记； 每个节点还关联了一个可能的标签sk的先验子集lk∈L。 标记是一个应用L：S↦L，它为每个对象sk∈S分配一个标记L(sk)∈lk。现在让我们对所有可能的标记L的类别引入兼容性限制R。具体地说，对于{L(si)，L(sk)}对属于给定集合Li,k Li×Lk的每个对(si，sk)结点中通过边连接的节点，R允许标记L。 通常，兼容性关系会减少可能标记的数量，如图16所示。
图16：使用三个节点S = [A，B，C]和三个标签L =(1,2,3)的简单示例说明放松标签。 (a)具有先验集LA，LB，LC和兼容性关系LAB，LBC的图形表示。 (b)所有可能的先验标签列表，其中第四和第五列上的星号分别表示LAB和LBC接受的组合。 两种兼容性关系唯一允许使用的标签是(1、2、3)和(2、3、1)，它们打印在灰色背景上。
这种二进制表示法的主要局限性是，兼容性关系通常要么太严格，以致不允许标记，要么太宽松，如图16所示，其中允许多个标记。因此，通常优选对这种框架进行模糊修改，其中标记p是数字pk(a)的矩阵，其中k = 1 ... N，a = 1 ... M，表示度将标签la分配给对象sk的置信度；这些数字必须满足约束
和
。数字pk(a)通常但不总是解释为概率。兼容性关系以实值函数ri,k(a，
)的形式表示； 它表示标签对象si与la和sk与l的兼容程度。人们通常应该给出兼容性，尽管对于某些应用程序，它们是从输入数据中学习的[146]。通过这些数量，可以引入与标记为p(定义为
)相关的所谓平均一致性a(p)；它测量分配给每个节点的标签相互一致的程度。
[147]中详细介绍了上述框架的一个有趣的概率解释，将松弛标记理论与图上的马尔可夫随机场优化理论联系起来[148]。 特别是，在[147]中显示，当将数量pk(a)解释为概率，而将ri,k(a，)解释为势时，则上面定义的平均一致性a(p)与 吉布斯分布的能量与有关的马尔可夫模型有关。因此，松弛标记的主要问题是找到使a(p)最大化的标记p，在MRF公式中，它对应于找到与最大后验概率相对应的构型。 当需要明确的标记时，将进一步的约束pk(a)∈ {0,1} 施加到最小化。
这样的最大化问题是NP难的，即不能在多项式时间内解决[149]。解决松弛标记问题的经典方法是从合理的初始标记p0开始，并使用一些类似于梯度下降的迭代方案来最大化a(p)[150,151]。但是，由于达到最佳状态需要大量的迭代，因此这种简单的方法通常很慢。为了开发更有效的算法并研究理论条件，通过有限的步骤就可以达到最佳收敛，已经付出了很多努力。最重要的方法是图扩散[152]，置信传播[153]，树的凸组合[154,155]，最大和扩散以及扩充有向无环图算法[149]。这些方法中的大多数都尝试最小化a(p)的上限，相对于a(p)的直接最大化，这在速度方面提供了更好的性能。 但是，它们的主要缺点是，从理论上不能保证它们收敛的点是所需的最佳值。
在轮廓检测的情况下，松弛标记的应用如下：首先构造一个图，其节点是输入图像的像素，其弧线链接相邻的像素(根据给定的邻域概念)。必须为每个像素分配一个标签(可以是二进制，实数或矢量值)，以指示给定点可以被视为对象轮廓的可信度。兼容性关系ri,k(a，)传达上下文信息；具体而言，ri,k(a，)对于共线的边缘对较高，而对于随机放置的边缘则较低。因此，最大化a(p)的函数pk(a)可以解释为轮廓的整体显着性。在实践中，通过使用局部边缘信息初始化标签，并迭代更新标签，以增强基础对象轮廓并抑制不期望的响应。在每次迭代中，每个标签都与其周围的标签相互作用，并且经过足够数量的迭代后，每个标签的值都由所有其他标签的值确定。这样，可以考虑全局上下文信息。最近的改进涉及在此框架中引入曲率[156]和纹理[151]信息。
总而言之，张量投票和张弛标记的两个框架提供了相似的算法，因为它们都归结为迭代方案，其中在每次迭代中，在存在共线边缘像素的长链的情况下，初始局部边缘强度得到了增强。松弛标记肯定优于张量投票的一个方面是，前者将轮廓检测作为优化问题而面临，并且依赖于更强的理论背景。因此，尽管张量投票可能会收敛到远离最佳值的局部最小值，但松弛标记可能有益于可用于马尔可夫随机场优化的退火程序，这有助于更接近全局最小值。
4.2.根据格式塔原理将像素分组为轮廓.
根据邻近的格式塔定律，良好的连续性以及最近的闭合[157](图17)和对称[158]，可以将边缘像素分为轮廓。 图论是用于此目的的自然数学框架：图G的节点对应于边缘像素，并且节点之间的互连建模连续边缘之间的潜在链接。 轮廓C由G的子图表示，并且通过最小化在G上计算的成本函数C进行检测。在本节中，我们将使用术语轮廓片段来表示该子图的连接组件。 成本函数C通常定义为节点突出项与C之间的总和，节点突出项是局部边缘强度的递减函数，而互连亲和力项则考虑了相邻边缘对之间的共线性和共圆性[159-161]]。
图17：按照(左)良好延续性和(右)闭合性的格式定律分组。
有关此方法的未解决问题有两个：
•虽然已经正式解决了通过最小化成本函数对图形进行划分的数学问题，但在计算上却很棘手。 因此，已经提出了各种各样的次优最小化算法，包括基于最小生成树[162]和Delaunay图[162,163]的计算方法。
•由于格式塔原则仅提供定性说明，因此将其转换为成本函数是任意的。
文献中已经提出了各种成本函数，包括几何模型[160]和概率模型[164]。最近，也得到心理物理学证据的证实[165,166]，在定义此类成本函数时也考虑了轮廓闭合[162,164,167,168]。轮廓封闭方法倾向于考虑更多的全局信息，并且能够检测虚幻的轮廓[169]。
关闭。通常，基于图的分组算法将闭包考虑在内，以y为周期的数学约束来识别G的子图G'，该子图G'使某个成本函数最小。在一些更高级的技术中，对G'施加了其他约束，例如凸度[170]或旋转指数，以防止自交叉循环[171]。例如，在[171]中，首先从边缘图上计算出一个稀疏连接的图G，方法是在邻近的格式塔定律和良好连续性的意义上，包括可能属于同一轮廓的连续边缘之间的弧。然后，检测到最短的非自相交周期并将其视为对象轮廓(因此，代价函数就是轮廓的像素数)。该方法不是很快，因为它的计算复杂度是O(n2logn)，其中n是边缘像素的数量。在[164]中提出了一种基于马尔可夫模型的更复杂的方法。具体来说，首先计算转换矩阵P，其中Pi,j 是包含边缘像素i 的路径也将包含边缘像素j 的条件概率。这些概率是根据[172]中提出的理论，根据邻近的格式塔定律和良好的连续性来计算的。结果表明，可以将P的特征值视为显着性度量，并且可以很容易地从P的特征向量(作为其强相关分量)中检测出周期。1 该方法比[171]中提出的轮廓检测方法更准确，并且速度更快，因为其计算复杂度为O(n2)。
1 A强连通分量C都是G'= V''
的子图，这样，只要从G中的节点j可以到达节点i，则节点j为也可从节点j到达，且i，j∈V'[173]。
通过[174]中提出的称为比率轮廓的算法，可以进一步提高速度和精度。与其建立边缘分布的概率模型，不如根据轮廓片段之间的间隙的标准化长度和所检测边界的总曲率将简单的成本函数最小化。该成本函数倾向于偏向带有短间隙的平滑边界。间隙的长度和曲率项均相对于G'的给定连接分量中的像素数进行归一化，以防止偏向小物体。参数入控制曲率项相对于间隙长度项的相对重要性。等高线的检测如下：与[164,171]相似，根据Gestalt的邻近性和良好连续性定律，通过链接边缘像素来构造图G。然后，在G中检测到使上述成本函数最小的循环，并将其视为对象轮廓。此方法比上面提到的其他两个方法快，计算复杂度等于O(n7/4)，并且可以更准确地检测轮廓。但是，其较高的性能是合理的。对没有理论依据的参数λ进行微调。
对称性：在更精细的方案中，通过寻找边缘像素组来考虑对称性，这些边缘像素在可能弯曲的对称轴周围表现出某种形式的全局或局部对称性。为了定义形状S∈R2的局部对称轴，引入了骨架的概念，通常将其定义为S的中间轴m。具体地说，将m定义为切线圆心的轨迹至少要在两个点上到达S的边界，而不接触S的内部(有关主题的概述，请参见[175，176])。根据定义，中间轴的点与形状边界等距，从而检测出局部对称性，如图18(左)所示。但是，众所周知，骨架化算法相对于输入形状S的扰动极为不稳定，因此会导致许多额外的尖峰偏离所需骨架，如图18所示。骨架的正确定义[177-179]。
图18：手的(左)合成和(右)真实形状，以及相应的中间轴。
[158]中提出了一种基于图形的方法，根据上述对称性定义对边缘像素进行分组。引入了一个新的成本函数作为两个项之间的比率：分子测量寻找的对称区域R的对称度，而分母等于R的面积。为了保证检测到的结构的对称性，引入分组令牌，将其定义为由先前检测到的边缘段构成的对称梯形。因此，分组算法将闭合边界标识为梯形序列，从而使上述成本函数最小。该方法能够在多项式时间内识别对称对象的边界，并且不会因成本函数的分母而偏向较小的对象。但是，它仍然很慢，因为其计算时间为O(n5.5)，其中n表示线段的数量。在[180]中提出了一种更快的方法，其计算复杂度为O(n2)。但是，它偏向小对象，并且在优雅且易于解释的成本函数的意义上不是最佳的。在[181,182]中提出了更详细的对称对象检测方法，该方法与上述方法不同，使用其他纹理信息来识别在3D世界中对称但由于透视而导致图像不对称的对象歪斜。
与前面小节中讨论的许多方法(它们仅提供彼此不相关的边缘像素的二进制图)相比，此处引用的分组方法生成像素组，其中一组成员属于同一轮廓。 通过这种方式，它们提供了对对象识别更有用的信息。 但是，上述技术的主要缺点是它们的计算复杂度。 为了提供快速算法，已经进行了许多研究。 例子是形态学方法，它基本上趋向于通过方向性膨胀[183,184]和基于边缘之间某些距离函数的聚类算法来填充轮廓线段之间的间隙，该算法考虑了它们的接近度以及它们的共线性和同圆度[185,186]。 对于边缘分组算法的概述以及对分组算法应具有的属性的最新讨论，请参考[10,187]。
4.3.活动轮廓
一般概念。主动轮廓，在文献中也称为蛇形或可变形模型，已在[188]中引入作为轮廓定位和交互式轮廓检测的变体方法。
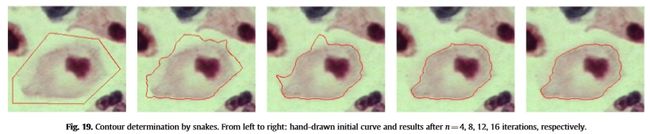
想法是通过最小化能量函数E(图19)来形成用户围绕对象O绘制的曲线C。通常，能量E由两个项的总和得出：内部能量Eint测量C的平滑度，而外部能量Eext考虑C与O的实际轮廓有多接近。在标准公式中，我们有Eint=
和Eext=
，其中a和β是输入参数，g是一个递减函数，当
→o时g()→oo。通常，选择形式g()=(1+p)-1，其中p为正参数。 Eint的两个项分别与C的长度和总曲率有关。另一方面，当C位于梯度幅度的最大值时，它为低。对于β= 0，可以证明上述函数可以重写为Lg(C)=
，其中ri(s)，i = 1，2 是向量的分量，张量gi,k(r)是向量的函数。输入图像I(r)(有关详细信息，请参见[189])。 Lg(C)解释为黎曼空间2 中曲线C的测地线长度，其度量由输入图像确定。这个重要的结果将蛇理论和几何模型联系在一起，而蛇理论和几何模型在本质上是拓扑独立的[189]。
2.黎曼空间是度量空间，其中点r =(x1，xn)和 r + dr =(x1 + dx1，...，xn + dxn)之间的无穷小距离由
给出。 张量gi,k(r)完全定义了R的度量。对于
，R缩减为普通的欧几里得空间。
图19.用蛇确定轮廓。从左到右：分别绘制n和4、8、12、16次迭代后的手绘初始曲线和结果。
主动轮廓算法可以根据曲线C的表示方式分为两种类型。在参数蛇中，曲线由其参数方程r = r(s)表示，其中s∈ [0,1]和r(0 )= r(1)。变量s表示点r(0)和r(s)之间的曲线部分的弧长与整个曲线的长度之比。在水平集蛇中，C由函数
(r)表示，该函数定义为C[190]上(r)= 0。这两个公式之间的主要区别在于处理拓扑变化：对于参数蛇，曲线C在其演化过程中保留其拓扑，除非在算法中集成了复杂的拆分和合并过程。水平集蛇更适合于拓扑更改，这在事先不知道必须检测的对象数量的情况下很有吸引力。但是，这会使该方法对噪声的鲁棒性降低，因为蛇会过度分裂。因此，也提出了拓扑保留级别集蛇模型[191,192]。对于最近对定级蛇的调查，我们参考[193]。
对于第3节中讨论的局部边缘检测器，蛇形模型具有几个优点，例如可以对检测到的轮廓施加连续性，平滑性和闭合性约束。而且，这些技术能够检测虚幻的轮廓[188]，这对于局部边缘检测器而言是不可能完成的任务。另一方面，E的最小化有几个缺点，例如对初始条件的依赖性强，收敛速度慢以及检测低对比度轮廓的能力差。为了克服这些缺点，文献中已经提出了对功能性E 的多种修饰。例如，傅立叶蛇[194]，有限元蛇[195]，双蛇[196]，模糊跟踪[197,198]，多分辨率方法[199]和受静电原理启发的模型[200]。在[201]中，已经提出了取决于边缘方向的外部能量。彩色图像的主动轮廓模型已经在[202]中提出。最近，大多数这些技术已在称为“联合蛇”的框架中统一[203]。有关概述，请参阅[204,205]。
与活动轮廓关联的扩散方程。 一个重要的发展涉及E的最小值与形式为
的扩散方程的解之间的等价关系，其中驱动力
将蛇吸引到物体轮廓上。 一旦外力不被限制为某个能量函数的梯度，该公式将变得比最小化E更通用。 此类模型的一个相关示例是所谓的梯度矢量流[206, 207]。 在[206]中，通过将
作为初始条件，将外力定义为另一个非线性扩散过程的最终状态。 与标准蛇形模型相比，GVF的主要优势是具有更好的将蛇形移入边界凹面的能力。
基于区域的活动轮廓。 大多数上述方法的局限性是通过梯度幅度来计算的。 使用此数量的缺点有两个：
•| ∇I|在低对比度的轮廓上取低值，从而使蛇塌陷[208]。
•| ∇I|在有噪声的情况下，蛇可能会很强壮，从而使蛇被不希望的局部极小值所吸引[209]。
这些问题可以通过引入防止塌陷的气球力来克服[195]，或者用更复杂的轮廓显着性代替梯度幅度[209]。 但是，一种更有效的方法是将E计算为C内区域而不是边界上的积分之和。 基于区域的蛇[210-212]对图像退化更健壮，对初始化更不敏感，因为有关基于轮廓的蛇涉及更多的全局统计信息。 此外，基于区域的蛇可以更自然地与纹理模型集成[213]。
就其本质而言，基于区域的蛇与Mumford-Shah机能密切相关[44]。在[211]中，假定输入图像是逐段恒定亮度曲线U(r)的嘈杂版本，该曲线仅在两个未必相连的区域
in和out上采用两个值c1和c2。通过最小化E = Eint + Eext形式的函数来检测in的边界C：Eint是C的长度和in的面积的线性组合； Eext是拟合误差的加权方差，表示为
，权重为入1和入2。权重 入1和入2 表示当输入图像 I(x，y)分别偏离in和out中的常数c1和c2时要支付的成本。我们观察到，驱动力而不是寻找具有最大| ∇l的点，而是使蛇趋向于使in和out的同质性全局最大化的配置。这些想法也已扩展到多级[214]和彩色[215]图像。通常，基于区域的蛇比基于轮廓的蛇具有更好的分割性能，并且对初始化的依赖性较小。但是，由于对双积分的计算，它们在计算上的要求更高。
基于形状的活动轮廓。最后，我们简要讨论在活动轮廓的上下文中引入形状分析。想法是在E上增加一个术语Eshape，该特权赋予Cand一组训练对象[216，217]之间的相似性。我们假设训练形状在缩放，旋转和平移方面已经彼此对齐，以使它们的重叠最大化[217]。术语Eshape通过以下两个步骤计算：首先，所有形状的矢量化。对于主动轮廓应用，最流行的方法是计算向量，其分量是对应形状的所谓带符号距离函数[218]的值。3关于其他向量化算法[219]，该算法在数值上是稳定，可以成功处理高曲率点和拓扑变化[217]，并且在水平集的框架内具有自然的实现。第二步是估计形状空间中训练形状的概率分布p。然后，将Eshape计算为-logp(vc)，其中vc 是与蛇C的形状相关的向量。当进化的蛇C在训练数据库中的形状最频繁时，此术语最小。
3.S的有符号距离函数定义为S轮廓的距离变换与等于S内部-1和S外部1的项之间的乘积。
基于形状的活动轮廓模型经常与Mumford-Shah函数[220,221]结合使用。在这方面，对p的高斯假设具有使Mumford-Shah函数凸化的优势。另一方面，这样的假设太简单了，并且已经提出了更复杂的分布[220]。
只要要检测的对象的形状与观察到的训练形状足够相似，则添加术语Eshape会带来显着的改进，尤其是在检测复杂对象时。但是，它的主要局限性是形状空间的高维度。通常，这可以通过线性主成分分析来解决，但是有符号距离函数相对于线性运算并不会关闭[217]。因此，线性PCA并不是最佳解决方案，这在基于形状的活动轮廓领域仍然是一个悬而未决的问题。
4.4.讨论
本节中回顾的上下文和全局轮廓检测器可分为两类：(i)通过考虑一些上下文信息来计算轮廓显着性，然后通过对显着性进行阈值提取边缘，以及(ii)直接识别有意义的结构。
关于前者，最重要的研究领域是张量投票和张弛标记。两者都可以看作是人类视觉系统中发生的抑制和促进现象的数学模型。尤其是，张量投票方案中涉及的向量和张量场具有生物学上的对应关系，称为关联场，在人类视觉中起着核心作用。至于松弛标记，图G中的节点和边缘可以分别解释为神经元和突触互连，而标记向兼容状态的演变有效地模拟了人类视觉系统神经元中发生的射击机制[ 143]。在这方面，应该指出的是，在最初的表述中，仅考虑了促进机制，而后来包括了抑制作用[222]。
对于后者，通常直接从输入图像中识别出有意义的结构通常被视为优化问题。 根据它们是依靠连续公式还是离散公式，我们将它们分为两类算法。 在第一种情况下，我们在第4.3节中介绍了变分方法，其中曲线根据与相关功能相关的欧拉-拉格朗日扩散方程式演化。 在4.2节中讨论的第二类包括根据格式塔原理进行边缘分组的技术，其中优化是通过动态编程技术在基于图的框架中执行的。 出于以下几个原因，可变活动轮廓肯定比格式塔分组方法更受欢迎：
•相对于离散的问题，可以以连续的方式更轻松，更优雅地提出计算机视觉问题；
•微分和变分微积分提供了比图论更强大的工具；
•活动轮廓框架自上而下，格式塔分组自下而上；
•活动轮廓框架已成功地应用于与轮廓检测有关的领域，而格式塔原理不适用于该领域(例如，从3D模型进行对象检测)。
另一方面，基于边缘分组的算法本质上不受监督，而大多数现有的活动轮廓技术需要用户进行初始化。 尽管已经进行了大量研究以实现对初始化的不敏感性(例如参见[200, 223])，但是仍不清楚这些方法的鲁棒性，特别是对于存在纹理和噪声的通用轮廓检测器而言。
在离散情况和连续情况下，基于给定成本(目标)函数(al)的优化的轮廓检测都非常强大，因为它可以有效地使用全局信息，而且功能多样，因为可以调整成本函数针对不同的应用。特别地，可以修改成本函数，以包括关于检测到的物体的一些先验信息，例如形状或对称性。另一方面，这种方法的主要缺点是成本函数一旦不凸，就可能会达到局部最小值，而不是全局最小值。对于高维搜索空间和非常复杂的成本函数，此问题变得尤为严重，为此，不希望有的局部最小值的数量可能会迅速增加。
5.多分辨率方法
上一节中讨论的许多运算符都有比例或分辨率参数，该参数与邻域的大小有关，该邻域的大小被认为是用于检测局部特征。在本节中，我们讨论多分辨率分析。它在轮廓检测中的重要性有两个：
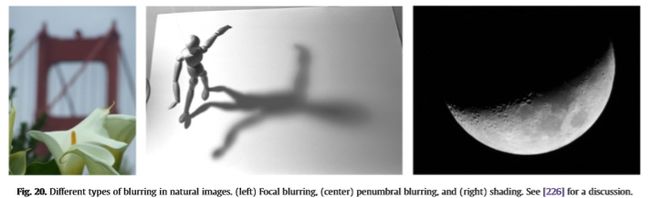
•自然图像包含边缘具有不同程度的模糊(图20)；
•有心理生理学证据表明人类视觉系统分别分析频域的不同部分[224,225]。由于边缘是根据人类观察者的感知在操作上定义的，因此无法忽略多分辨率方面。
5.1小节概述了有关多分辨率分析的一般事实，而特定的多分辨率轮廓检测器将在5.2小节中讨论。
图20：自然图像中的不同类型的模糊。 (左)焦点模糊，(中)半影模糊和(右)阴影。 参见[226]进行讨论。
5.1.多分辨率分析
尺度空间。 小波理论[227–229]是一种用于多分辨率分析的自然数学框架：在线性情况下，输入图像I(r)与函数ψs(r)的一系列缩放版本ψs(r)卷积。 叫小波母； s是分辨率或比例参数。 这些卷积的输出产生一个3D对象I(r，s)= I(r)*ψs(r)，称为线性比例空间(图21)。 由于几种数学特性(例如各向同性，可分离性，熵最小化，没有过零创建[230]，线性扩散方程∂I[231]的解决方案，半线性等)，最著名的母小波ψ是二维高斯函数。 群属性，以及噪声抑制的次最优性 ∂I/∂s=∇2I，局部最大值的单调性[73]。
图21：高斯比例尺空间的示例：一个输入图像和具有高斯函数的卷积的多个输出，分别为σ= 2、4、8、16。 高斯函数的方差满足比例参数s的作用。
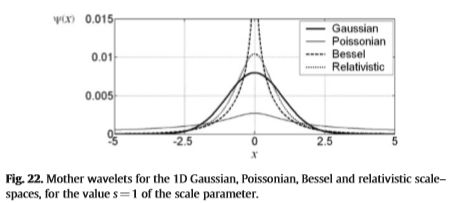
非高斯线性比例空间。直到最近，人们普遍认为高斯函数是唯一具有这种数学特性的函数，并且已经提出了尺度空间理论的几种公理表述(有关概述，请参见[232，233])。但是，正如[234，235]所指出的，只要不再要求平滑核具有有限方差，与上述公理公式兼容的非高斯尺度空间也是可能的。相关示例是单基因尺度空间[236，237]，贝塞尔尺度空间[238]，相对论尺度空间[239]，Gabor尺度空间 4 和 a-尺度 空间[240，241] (图22)。 a-尺度 空间满足线性扩散方程∂I/∂s=-(-∇2)aI。对于a = 1和a = 1/2，该方程式分别简化为高斯和泊松情况。对于其他a-尺度 值，小波表现出更复杂的兴奋性和抑制性区域模式，类似于哺乳动物视觉系统的外侧膝状核细胞和视网膜神经节细胞的经典中心-周围感受野中存在的那些[234，242]]。 这个事实使a尺度空间对大脑的前端视觉系统建模具有吸引力。
4 在一维情况下，通过将输入信号I(x) 与复函数
卷积来获得Gabor尺度空间。严格来说，这是公理意义上的标度空间，当且仅当λ为常数且标度参数σ在0到∞之间变化时。但是，应在许多多分辨率应用程序中注意比例空间的半群性质。对于多重Gabor滤波器也有类似的考虑，参数λ与σ成比例，这违反了尺寸的情况。
图22.一维高斯，泊松，贝塞尔和相对论尺度空间的小波，尺度参数的值s = 1。
非线性尺度空间。对于比例参数的高值，由于高模糊，I(r，s)对输入图像I(r)中的噪声具有鲁棒性。这一事实使尺度空间理论对正则化和反问题具有吸引力[243、244](有关调查，另请参见[9、245])。另一方面，在边缘拖尾方面要付出很高的噪声抑制，并且在线性框架中无法解决该问题。因此，已经引入了几种非线性尺度空间。重要的例子是仿射不变尺度空间[57]，形态尺度空间[8、246、247]，变尺度空间[245]和Lee理论尺度空间[248](它们是从非线性扩散方程派生的)和尺度从非线性小波[249-251]导出的空间。对于这些比例空间的调查和讨论，请参考[252-254]。
5.2.比例尺空间中的轮廓检测
图23.一维示例中比例尺空间中边缘的行为。 (左)嘈杂的亮度曲线I(x)，(中心)其高斯比例尺空间I(x，s)，显示为(x，s)空间中的强度图，(右)位置(x)拉普拉斯算子在不同比例尺上的零交叉点。
刻度空间中边缘的行为已得到详尽的研究[255，256]。 在图23中示出了一个有噪声的一维信号l(x)，为其计算了高斯比例空间l(x，s)，并且将边缘检测为
的零交叉。 随着比例参数的增加，归因于纹理和噪声的拉普拉斯算子的零交叉消失。 另一方面，尺度越大，拉普拉斯算子的零交叉点的边缘定位能力越差。
边缘聚焦。结合粗糙和精细比例尺优点的一种常用方法是边缘聚焦(EF)[257-260]。它包括以一定的粗略尺度Smax检测边缘，在该尺度上噪声的影响可以忽略不计，并通过(r，s)空间向下跟踪它们，直到边缘被很好地定位的精细尺度Smin。图24示出了用于2D示例的EF。这个想法已经以几种方式发展起来：在[261]中，提出了一个概率模型，其中马尔可夫过程考虑了从粗到细的因果关系。在[131，262]中，EF不是逐像素执行的，但是考虑了关于对象轮廓的连通性信息。在[263-265]中描述了基于EF的蛇。在[129，130]中，EF与生物学动机的纹理抑制方案相结合，在[266]中，EF被应用于彩色图像。在[267，268]中，表明EF可用于测量整体对比度和轮廓的扩散程度。
图24. 2D图像的EF示例。第一行：分别为σ= 8、4、2、1的Canny边缘检测器的输入图像和输出。第二行：分别从标度σ= 8到标度σ= 4、2、1跟踪的边。
EF可以针对各种输入图像成功实现高噪声抑制和良好的边缘定位。但是，它有几个限制：
·高度突出的轮廓可以生存到非常粗略的比例的假设不一定是正确的。例如，即使彼此靠近的边缘在比例尺参数增加时也可能迅速消失，即使它们在输入图像中高度突出(例如，参见图21中高尔夫球车的杆)。
·对于2D信号，尺度空间中奇异点的复杂拓扑结构[68]使该方法在计算上没有吸引力[226]。
·EF的输出关键取决于Smin和Smax的值，这些值不是由一般原理得出的。此外，为了获得良好的结果，这两个参数需要为输入图像的每个像素取不同的值(尤其是Smax)。
自适应比例参数。关于后一点，已经做出了一些努力，以开发具有与位置有关的比例参数s = s(r) 的边缘检测器。关键思想是通过s = s(r) 空间中两个表面的交点获得边缘：第一个是由比例相关的运算符在不同比例下检测到的边缘曲线所描绘的；第二个只是s(r) 标尺的位置相关选择。这两个表面在 (r, s) 空间中以3D曲线相交，其在xy平面上的投影定义了检测到的轮廓。因此，比例尺选择机制被简化为s(r) 的定义。
一种定义的简单方法是为每个像素计算所谓的最小可靠比例，这是保证SNR高于可接受阈值SNRmin的最小比例。但是，这样的定义只会将问题转移到另一个域：由于必须测量每个像素的局部邻域N(r)内的噪声量，因此需要确定N(r)大小的新比例参数。介绍。此外，SNRmin的选择是启发式的。在[269]中提出了另一种解决方案：s(r)是通过将非最大值抑制推广到尺度空间来确定的。但是，这样的过程是基于输入亮度分布的临时归一化。通常，基于位置的比例参数的轮廓检测器对于包含边缘具有不同模糊水平的图像，其性能优于EF(图25)。但是，选择是基于启发式方法[269,270]或有关输入图像的某些附加信息，这些信息可能并不总是可用的(例如，范围数据[271]或用于获取输入图像[226]。
图25.多分辨率轮廓检测。 从左到右：输入图像； 对于σ= 1，Canny边缘检测器的输出，在模糊边缘上显示多个响应；对于σ= 4，Canny边缘检测器的输出平滑尖锐边缘； [269]中提出的多分辨率方法的输出，结合了两者的优点。
总之，多分辨率轮廓检测可分为边缘聚焦和位置相关的模糊。边缘聚焦可以实现高噪声抑制和良好的边缘定位。可以将其视为自上而下的全局方法，它比自下而上的全局方法(例如显着性计算或分组)对噪声的鲁棒性更高。另一方面，其主要缺点是标度空间奇点的复杂拓扑结构使该方法在计算上没有吸引力。对于包含不同模糊程度的图像，与位置有关的模糊通常优于边缘聚焦。但是，一旦跟踪边缘直到与位置相关的最小标度，这些方法就可以与边缘聚焦结合使用。
6.绩效评估
严格比较不同轮廓检测器并研究其输入参数的影响需要进行定量性能评估。尽管它很重要，但是在轮廓检测的大多数已发表工作中都没有进行定量性能评估[272,273]。由于所有提议的方法都有不同的缺点，因此，关于如何进行绩效评估尚无普遍共识。此外，轮廓检测器的质量可能取决于其部署的特定任务[274]。本节回顾了最常用的定量绩效评估程序。
6.1.一般方法
第一个问题涉及进行定量绩效评估的一般方法，尤其是是否应使用地面真实性(GT)，即轮廓规格。在[275,276]中，通过测量所检测轮廓的各种属性(如相干性，连续性，平滑性和良好的连续性)来评估所检测轮廓的质量。该方法具有客观的优点，但是不考虑检测到的轮廓和输入图像之间的一致性。特别是，虽然人类观察者会认为相关输出的质量较差，但使用这些性能指标可以使输入图像过度模糊的边缘检测器得分很高[273]。相反，在性能评估过程中与人类观察者的共识是通过基于对检测轮廓质量的主观评估的性能指标实现的[273]。这基本上是通过执行心理物理实验来完成的，在该实验中，人类观察者必须判断所检查的轮廓检测器的输出质量。但是，这些方法很昂贵并且不能自动执行。
由于这些困难，大多数作者将检测到的轮廓像素DC集合与为像素指定给定输入图像的期望输出的地面真实像素GT进行比较。为了获得客观的GT，在早期工作中，该方法仅应用于合成图像[277,278]。在[279]中已经提出了对这样的GTs 的自动估计。然而，综合输入的高分并不一定意味着自然图像的良好性能[280]。因此，最近也对自然图像进行了基于GT的定量性能评估[2,281]。为此，已经生成了带有相关GT的自然图像的几个数据集(图26)。例如，伯克利(300张图像)[2]，南佛罗里达(50张图像)，索尔比(100张图像)[124]，Corel(5000张图像)[282]和RuG(40张图像)[22]数据集。为了克服地面真理的主观性，一些数据集为同一幅图像提供了不同的地面真理，与不同的人类观察者相关联[2]；以这种方式，可以在不同的观察者上平均给定输入图像的给定算法的性能。但是，由于在大多数情况下，观察员的数量几乎不超过四到五个，因此这种类型的定量绩效评估仍然相当主观。此外，仅包含几百个图像的数据集是否具有足够的代表性还不是很明显。
图26：第一行：来自RuG数据集的自然图像[22]。 第二行：对应的GT。
总而言之，基于GT的绩效评估无疑是最受欢迎的方法，因为这似乎是完全客观和完全主观的定量绩效评估方法之间的良好折衷。尽管对于依赖于任务的轮廓检测来说，这可能是最佳选择，因为可以生成合理的客观地面真实情况，但对于通用应用而言，最可靠的方法仍然是人类观察者的直接评估。在这方面，尽管存在上述缺点，但由于其在人工方面的成本降低，因此经常与地面实况进行比较，如果经常被部署为次优解决方案。
6.2.性能指标
现在，我们要解决量化DC和GT之间的(不)相似性的问题。 在检测到的轮廓和基本事实之间广泛使用的相似性度量是普拉特的功绩图，定义为FoM=
，其中dGT是GT的距离变换，而d0是比例参数。 FoM取(0，1]中的值，如果DC与GT重合等于1，并且相对于DC和GT不对称。比例参数d0控制FoM对GT和DC之间差异的敏感度： d0，仅当DC非常类似于GT时，FoM才接近1；而对于d0较大的值，GT和DC之间的较大差异是可以容忍的。
FoM通过考虑假阳性(即等高线图中存在不期望的响应)，假阴性(即等高线)以及移动或变形的量，对给定等高线图的质量进行整体评估。 从GT位置正确检测到轮廓。 在这种方法中，根据输入图像的测试数据集的FoM的统计分布比较了轮廓检测算法(图27)。 其他全局度量是在[2]中引入的 F度量 和在[22]中引入的 p系数 ，这与Pratt的FoM相对于DC和GT，Haursdoff距离[283]，Odet差异[284]对称 和Chernoff熵[124]。
图27.对于四个不同的轮廓检测器，在RuG [22]和Berkeley [2]数据集上计算的FoM值的统计分布：Canny边缘检测器[73]，结合了不同局部特征的局部方法EDISON [ 123]，一种仅采用环绕抑制的上下文方法[128]，以及一种更先进的全局方案，它同时利用抑制和格式塔边缘分组[184]。复杂程度的提高对应于结果的性能改进。
上面提到的全局品质因数的主要缺点是，没有提供有关差异来源的信息：假阳性，假阴性或轮廓偏移。面对这个问题，一种众所周知的方法是使用召回率R =
和精度P = 
作为性能指标。它们分别测量正确检测到的轮廓像素(card(GTnDC})相对于给定运算符检测到的所有轮廓像素的数量(card(DC})或GT轮廓像素的数量(card(GT))的比例。但是，由于在地面真实情况下手绘轮廓相对于它们在输入图像中的确切位置可能存在位移误差
，所以即使完全不存在假阳性和假阴性，设置的 GTn DC 也可能为空。实际上，通过将集合 GTnDC 替换为DC到距GT的点的距离小于固定阈值0的那些DC的集合来计算略有不同的数量。
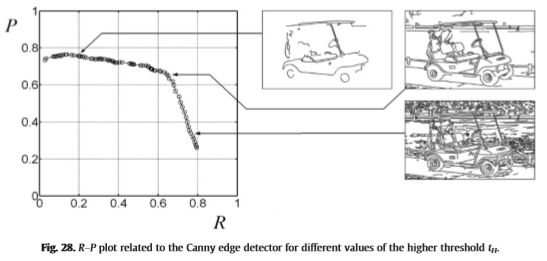
通常使用查全率和精度来研究输入参数对给定轮廓检测器性能的影响。具体地，当输入参数p改变时，在类似ROC的图中相对于彼此绘制函数R(p)和P(p)。对于Canny边缘检测器和给定的输入图像，图28描绘了一种典型情况，其中输入参数p是较高的阈值tH。由于R-P图在不同的图像上可能会有所不同，因此习惯绘制在数据集的多个图像上计算出的平均函数
和
，其中Ri(p)和Pi(p)是与第i个图像相关的召回率和精度分别。通常，由于许多错误的否定因素，较高的精度值与较低的召回率会同时出现。反之，以许多误报为代价获得较高的查全率，从而降低精度。 R-P图与ROC图有一些相似之处，因为两者均用于量化良好检测(低误报)和良好噪声抑制(低误报)之间的折衷。但是，精度和查全率具有比例不变的优点，因为归一化分母随图像的线性大小线性增加，而不是像ROC那样呈二次方增长。
图28：对于较高阈值tH的不同值，与Canny边缘检测器相关的R-P图。
通过对函数R(p)和P(p)进行简单的微分分析，可以确定参数p的最优值popt。在下文中，我们假设精度和召回率是同等重要的，即，必须以相等的查全率来弥补精度的小损失，反之亦然。 5 很容易看出，在R-P图上其切线的角系数等于-1的点已经达到。
5当不是这种情况时，用新的量P'=λP 和R'=μR 替换P和R就足够了，其中选择系数λ和μ，以便对于该特定任务，P'和R'同样重要。
到目前为止讨论的性能指标取决于规模参数FoM的 -d0 和 P和R—在这里通常用σ0表示。尽管这种依赖性在文献中经常被忽略，但它强烈影响定量性能评估的结果，因此无法比较不同作者获得的绩效指标的值。我们已经研究了这种依赖性，结果是这些性能指标与logσ成比例增长。具体而言，通过为RuG数据集[128]的40个图像中的每个图像应用四个不同的轮廓检测器[73、123、128、184]，已生成N = 160个算法结果的集合S。对于每个算法结果，已针对X = 1 ..，10的不同值计算了上述相似性度量FoM和F，并令与第i个算法结果相对应的f(σ)值(为简洁起见，此处相同符号f用于表示指标FoM和F)的值。然后，我们计算了归一化的差异
并将其在所有N个算法结果中平均，从而获得函数
。对于FoM和F，在图29中绘制了这样的函数。正如我们所看到的，它们可以通过对数函数很好地近似，尤其是对于FoM。该结果允许将使用不同比例参数值执行的不同测量结果关联起来(图29)。
图29：FoM和F度量的函数(σ)的图，与对数模型非常吻合。
总而言之，文献中提出的将算法结果与基本事实进行比较的方法可以基于(i)单个性能指标和(ii)以及多个性能指标(如准确性和召回率)划分为多种方案。前者通常用来比较统计算法，根据统计分布，在不同图像上评估的品质因数进行评估，这些统计已针对输入参数进行了优化。应该注意的是，Pratt的FoM和Haursdoff距离考虑了检测到的轮廓线与地面真实情况之间的偏移和变形误差，因此对轮廓平滑的算法进行了惩罚。对于多个指标，通常针对某些输入参数的不同值将它们相互绘制，以说明不同目标之间的最佳折衷。除了这些考虑因素之外，没有理论基础或经验证据都倾向于使用特定的绩效指标。
7.计算复杂度
在本节中，我们讨论与上述轮廓检测算法的计算复杂度有关的一些方面。让我们首先考虑第3节中介绍的局部边缘检测器。它们中的大多数是基于线性滤波的，例如微分方法(第3.1节)，第3.2节中描述的某些统计方法以及局部能量和相位一致性的计算(第3.3节)。因此，计算复杂度与所需卷积的数量有关。在这方面，基于单基因信号的差分方法和算法最多需要三个卷积，因此比基于Gabor滤波器基于局部能量计算的方案要快，为此，所需卷积的数量与所考虑的数量成比例方向(通常至少六个)。
7.1.线性局部方法的复杂性
通常，卷积的计算时间取决于其具体的实现方式：对于不可分离的内核，直接在空间域中工作将需要O(Nσ2)，而对于可分离的内核(即内核w(x，y))则需要O(Nσ)。(核w(x,y) 可以表示为唯一x与唯一y之一的乘积w(x，y)= w1(x)w2(y))，其中N是输入图像中的像素数σ是比例参数。
当要求比例不变时，将其设为
，对于不可分离的情况，计算时间变为O(N2)，对于可分离的情况，计算时间变为O(N3/2)。另一方面，快速傅里叶变换允许独立于σ来计算O(NlogN)中的卷积，该卷积略小于O(N3/2)。人们普遍认为，在傅立叶域中的工作比在空间域中的工作快。然而，尽管在极限
中当然是正确的，但是当平滑可乐粉是可分离的时，这不一定是正确的。具体来说，对于有限的N，O(NlogN)可能与O(N3/2)非常相似，并且比例因子发挥了最重要的作用，该比例因子将计算时间与渐近复杂度相关联。对于傅立叶域，该因子是恒定的，而对于空间域，该因子与比例参数和输入图像的线性大小之间的比率r = σ/
成比例。因此，至少对于较小的r值，空间域的实现要快于频域的实现。 6通过计算图像的高斯尺度空间，给出了一个重要的示例，其中即使对于较大的r值，空间域也比傅立叶提供了更有效的实现。具体地，由于尺度空间的半群性质，输入图像和具有大σ的高斯核之间的卷积可以减少为具有小σ的几个卷积的级联。由于还需要中间标度来计算标度空间，因此在空间域中的总体计算复杂度要比频域低。还必须指出，对于某些滤波器，例如Canny标准意义上的最佳滤波器，可以使用快速IIR实现，其计算复杂度独立于σ为O(N)。
6例如，对于512×512图像，只要σ≥6，则在空间域中的工作要比频域中的工作快。
7.2.非线性局部方法的复杂性
在3.2和3.4节中回顾的非线性边缘检测器的计算复杂度高于上述线性方法。统计方法(第3.2节)要求针对每个像素和每个方向，对大约为σ2像素的总体进行统计两样本检验的计算，从而使总体计算复杂度为
，其中
是取向。对于基于VOS的算法(第3.4节)，通常认为从计算角度来看它们非常昂贵。但是，只有在部署了直接实现的情况下才是正确的。特别是，在线性大小为σ的邻域中排序像素需要O(σ2logσ)运算，这将使整体计算时间高达O(N σ2logσ)。但是，两个相邻像素(i，k)和(i，k + 1)的邻域N(i，k)和N(i，k +1)强烈重叠，并且只有两个1像素宽的像素带不同，线性大小O(σ);因此，当N(i，k)已被排序时，排序N(i，k + 1)减少了从大小为O(σ2)的有序集合中替换O(σlogσ)像素。使用二叉树，这可以在O(ologlo)操作中完成，因此减少了总体计算时间，减少到O(N σlogσ)，相对于在空间域中具有可分离内核的卷积，O(N σlogσ)略高。
7.3.非本地方法的复杂性
最后，我们转到第4节中讨论的上下文方法和全局方法。由于大多数方法都是迭代的，因此它们的计算复杂度要高于局部方法，并且主要由达到收敛所需的迭代次数Niter决定。 用于基于扩散过程的算法，例如主动轮廓或张量投票。 Niter强烈依赖于停止规则及其参数，并针对不同的图像敏感地进行更改。 通常，对于这些方法来说，甚至很难使Naer达到上限。 另一方面，对于基于图的方法(例如第4.2节中描述的格式塔分组方法)，我们可以指出Niter随输入图像的大小呈多项式增长。 示例是[164，171，174]中提出的检测封闭结构的方法，其计算复杂度分别为。 o(n2logn)，O(n2)和O(n7/4)。
8.总结，讨论和结论
在表1中，我们给出了面向边缘和直线的轮廓检测算法的分类法。我们的主要区别在于本地方法和全局方法之间。前者主要基于差分，统计和局部傅立叶分析，旨在检测图像中亮度，颜色和纹理的局部过渡。它们中的大多数都是快速的，概念上简单直观，并且易于实现。但是，它们无法捕获中级和高级视觉提示，例如良好的连续性，轮廓闭合，形状和对称性。这些缺点可以通过上下文和全局技术来克服，这些技术远远超出了对每个像素的局部邻域的简单分析。基于环绕抑制和简化，我们将它们分类为计算轮廓显着性的算法，根据良好连续性，闭合性和对称性的格式塔定律以及有效轮廓将边缘像素分组为共线响应的长链。全局方法比局部方法具有更高的性能，但在计算上也要求更高。大多数本地和全局方法都可以单分辨率和多分辨率方式实现。我们将将不同尺度的输出组合为(i)边缘聚焦和(ii)使用局部尺度参数的策略进行分类。前者在良好的定位和良好的噪声抑制之间提供了极好的折衷，而后者则更适合检测具有不同模糊的轮廓。实现这两种技术优点的最佳方法可能是通过刻度空间跟踪边缘和轮廓，直到找到与位置相关的刻度o(r)而不是固定的刻度。
8.1.取决于输入参数
所有上述轮廓检测方法的一个关键方面是用户需要指定几个输入参数。他们的选择极大地影响了轮廓检测的结果，没有通用的值可以为每个输入图像带来良好的结果。因此，已经进行了很多研究来减少输入参数的影响。提议的策略可以分为两类：
·多值方案，其中对参数p的[pmin，pmax]范围内的N个不同值p1 ..... pN多次应用相关算法，并使用补充技术来组合结果。例如边缘聚焦[257]，磁滞阈值[73]或[184]中提出的多阈值方法。这些方法实际上增加了要指定的输入参数的数量，因为用户必须提供pmin，pmax和N的值，而不是唯一的值p。但是，相对于单值情况，多值算法通常对pmin，pmax和N的值不太敏感，并且更容易找到一个范围[pmin，pmax]，该范围对于大量输入图像产生良好的结果。而且，由于利用了同时使用p的大和小值的优点，因此获得了更好的性能。
·包括对输入图像进行进一步分析的方案，旨在为该特定图像计算相关参数p的最佳值。在某些情况下，p的值是针对输入图像的每个像素本地计算的，而不是针对整个图像全局计算的(例如，[269,288])。尽管这些方法可以改善结果，但从理论上讲，它们的主要问题是，为优化某个参数p而部署的子算法需要从用户引入其他输入参数。因此，他们只是将参数选择问题从一个域移到了另一个域。
我们对两个参数进行注释：(i)部署用于提取局部边缘特征的窗口的大小s(比例参数)，以及(ii)与边缘强度进行比较的阈值。
对于单分辨率方法，比例参数的值由在使用s的大值实现的噪声抑制与良好的定位之间的权衡来确定，对于s的较小值可以得到更好的结果。第5节中介绍的一些多分辨率技术尝试根据输入图像自动确定比例参数。例如，在[269]中，局部尺度参数是从尺度空间中执行的非最大值抑制的一般化获得的。但是，需要引入一个新的参数
，该参数涉及不同比例的边缘强度，其选择不是从一般原理中得出的。基于边缘聚焦的其他多尺度方法的特征在于两个尺度参数smin和smax，它们是平滑窗口大小的最小值和最大值。尽管它们的选择主要是启发式的，但相对于单分辨率方法，通常边缘聚焦方案受smin和smax值的影响较小。
我们将要讨论的第二个输入参数是阈值T。尽管将其值调整为单个图像相对容易，但实际上不可能找到T的通用值，T对于每个输入图像都能产生可接受的结果。因此，已经进行了大量研究来开发从输入图像自动确定阈值的算法。最简单的方法是分析必须进行阈值处理的边缘特征f的直方图H，并寻找双峰性，从而将阈值T置于两种模式之间的局部最小值。但是，在大多数情况下，有关的直方图远不是多峰的。其他作者建议在贝叶斯框架中确定最佳阈值。具体地，输入图像的所有像素的集合被划分为边缘和非边缘响应的类别A和B。然后，令pA(f)和pB(f)分别为A和B类的f的条件概率分布，PA和PB为相关的先验概率，最优阈值由值fopt给出，其等式为PApA( fopt)=PBpB( fopt)成立。在此过程中，最困难的任务是确定pA(f)和pB(f)。一些作者通过对pA(f)和pB(f)(p1(f)和p2(f)最常用的分析形式)的一些分析假设，从f的直方图H估计pA(f)和pB(f)。分别是瑞利，X2和伽玛分布[289])，但是很难用简单的分析形式对pA(f)和pB(f)进行建模，从而削弱了阈值的最佳值。在其他工作中，pA(f)和pB(f)是根据手绘的地面实况[2，124]估算的，因此可以使用非参数模型。虽然这会带来一些性能上的改进，但是有两个重要的缺点：(i)结果阈值在一定程度上是主观的，因为不同的观察者会产生不同的地面真相，并且(i)假定图像数据集的地面真相是可用有足够的代表性，不一定是这种情况。由于这些限制，其他作者不愿对f进行统计分析，而是通过优化所得轮廓图的某些形态学特性(例如所得二进制图中连接成分的数量或平均长度)来确定fopt [ 290]。
总的来说，可以得出结论，输入参数的影响仍然是轮廓检测中的一个开放问题，并且当最近的复杂度被限制为使用相同的输入值时，大多数最新技术对于标准技术都带来很小的改善各种输入图像的参数。
8.2.计算步骤的相互依存
现有的大多数轮廓缺陷算法的另一个重要限制是，它们构成的步骤需要单独优化，而不是将整个过程视为一个整体(尽管有一些例外，例如一些基于马尔可夫随机场的方法)。该算法给出了一个重要的示例，以提取局部边缘特征，这些特征未按照后续步骤(例如，根据局部响应计算轮廓显着性或根据格式塔原理对边缘进行分组)来设计。特别是，已经进行了大量研究来区分共线边缘的长链和随机分散的定向刺激[136, 137, 291]。生物证据表明，人类视觉系统也采用了类似的机制[139, 140]。然而，即使当输入图像仅仅是随机噪声时，利用大多数现有局部技术提取的局部边缘方向也显示出高相关性。 7 这意味着由对象轮廓和噪声或纹理引起的边缘往往会很好地连续，从而削弱了上述后处理技术的有效性。总而言之，我们认为轮廓检测方案的更精细的优化(其中考虑了不同子算法的相互依赖性)将导致相当高的有效性和效率。
7更准确地说，令ϕ(r) 为白色随机噪声n(r)的高斯梯度的正交方向。然后，h(r)沿局部边沿方向定向的概率分布p( ϕ(r + h(r)) − ϕ(r)) 即使对于|h|>2σ也显示出明显的峰值。
8.3.形状信息的重要性
最近取得的主要进展是引入了有关要检测轮廓的先验形状信息，因此将仅检测某些给定形状的轮廓。这些方法的主要优点是它们能够在强烈遮挡的情况下检测物体，并同时拒绝不希望的轮廓，例如由于锐利阴影或不感兴趣的物体而产生的轮廓。不利用形状信息的局部甚至全局方法显然不足以完成此任务。此外，形状分析可以更好地抵抗图像失真(例如噪声和模糊)。基于形状的轮廓检测通常被表述为优化问题，其中要最小化的成本函数包括考虑到检测到的轮廓的形状与所需形状之间的差异的项。这种术语表示为似然比，它是通过密度估计技术从形状数据集中学习的。
表1：文献中提出的主要轮廓检测器的拟议分类法。 对于每个班级，其主要功能都在括号中指出，并且提到了最具代表性的文章。
本地方法 微分(简单，速度快) 基本概念[62]；零交叉Marr-Hildreth，[64,65,68]；最佳边缘检测，Canny，[73-76]；本地装修[81-83，85]
统计(纹理边界) 灰度分布[87-89]；颜色和纹理属性的分布[2,90]；梯度矢量场的分布[95,97]
相位一致(幂等) 正交滤波器，Gabor，[103,104,107,108]；单基因信号[109]；应用[104,110,113,114]
VoS和形态(颜色，盐和胡椒噪声) [118-120]
功能组合(优化) [2,123-125]
上下文和全局方法
显着性(低对比度轮廓) Surr, suppr 和便利化[22,129,137,285]；张量投票[133，135]；放宽标签[151,156,286]
格式塔分组(从边缘像素到轮廓) 良好的延续[10,159,160,287]；关闭[164,171,174]；对称性[158,180,181]；定向扩张[183,184]
活动轮廓(用户交互) 关键概念[12,188,189,193]；梯度矢量流[206,207]；基于区域的能源[210,211,213]；形状先验l216,219,221]
多分辨率方法 销售空间中的边缘行为 [68,255,256]
边缘聚焦(良好的定位和噪声抑制)[129,257,260,261]
局部比例控制(不同类型的模糊) [269,271]
尽管此方法在概念上很简单，但仍需要考虑几个技术方面：首先，形状空间的极高维度(在该维度上定义了成本函数)使得难以进行优化。解决这个问题的最简单方法是使用PCA或ICA，但是线性的假设通常过于简单(另请参见[217]中的讨论)。同样，整个形状应遵循先验模型的假设通常过于严格，并且在重要情况下，如果输入图像中感兴趣对象之间的相似性，则情况并非如此(例如对象遮挡)并且先验形状模型仅出现在图像的某些部分，这些方法将不会收敛到最佳状态。解决此问题的有效方法是将局部置信度图与先前模型关联，并仅在高置信度区域上约束检测到的轮廓[292]。通常，在轮廓检测中引入形状分析可显着提高性能，特别是对于专门解决特定问题的算法而言。但是，如今，它的成功仅限于感兴趣的对象在形状上与用于构建先前模型的观察到的训练示例足够相似的情况。
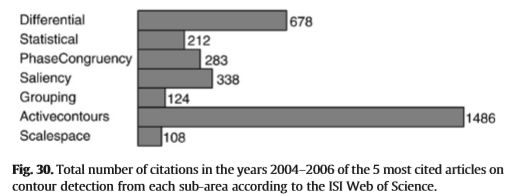
我们的主要结论是，考虑到多峰轮廓定义(通过亮度，颜色或纹理变化)，减少噪声和纹理的轮廓掩蔽影响的机制，感知分组，多尺度方面以及其他因素，轮廓检测已经达到了高度的成熟度和成熟度。 ，在某些情况下，还包括形状等高级视觉信息(图30)。 结果，多年来，在算法对参数值选择的鲁棒性方面已经取得了相当大的进步。 我们认为，研究和开发高视力操作的反馈方案具有实现进一步实质性进展的巨大潜力。
图30.根据ISI Web of Science，在2004-2006年间，有关每个子区域轮廓检测的5篇被引用最多的文章的引用总数。
参考文献
[1] S.Zeki,A Vision of the Brain,Blackwell Scientific Publications,Oxford, 1993.
[2] D.R.Martin,C.Fowlkes,J.Malik,Learning to detect natural image boundaries using local brightness,color,and texture cues,IEEE T-PAMI 26(5)(2004) 530-549.
[3] N.R.Pal,S.K.Pal,A review on image segmentation techniques,PR 26(9)(1993) 1277-1294.
[4] H.D.Cheng,X.H.Jiang,Y.Sun,J.Wang,Color image segmentation:advances and prospects,PR34(12)(2001)2259-2281.
[5] X.Cufi,X.Munoz,J.Freixenet,J.Marti,A review of image segmentation techniques integrating region and boundary information,Adv.Imaging Electron. Phys.120(2002)1-39.
[6] D.Ziou,S.Tabbone,Edge detection techniques-an overview,Int.J.Pattern Recognit.Image Anal.8(4)(1998)537-559.
[7] M.Petrou,The differentiating filter approach to edge detection,Adv.electron. electron phys.88(1994)297-345.
[8] P.T.Jackway,Morphological scale-spaces,Adv.Imag.Elec.Phys.119(2001) 123-189.
[9] O.Scherzer,Scale-space methods and regularization for denoising and inverse problems,Adv.Imag.Elec.Imag.128(2003)445-530.
[10] S.Sarkar,K.L.Boyer,Perceptual organization in computer vision:a review and a proposal for a classificatory structure,IEEE SMC23(2)(1993)382-399.
[11] K.1.Boyer,S.Sarkar,Guest editors' introduction.Perceptual organization in computer vision:status,challenges,and potential,CVIU 76(1)(1999)1-6.
[12] T.Mclnerney,D.Terzopoulos,Deformable models in medical image analysis:a survey,Med.Image Anal.1(2)(1996)91-108.
[13] S.Sarkar,P.Soundararajan,Supervised learning of large perceptual organization: graph spectral partitioning and learning automata,IEEE Trans.Pattern Anal. Mach.Intell.22(5)(2000)504-525.
[14] S.Wang.J.M.Siskind,Image segmentation with ratio cut,IEEE Trans.Pattern Anal.Mach.Intell.25(6)(2003)675-690.
[15] D.Comaniciu,P.Meer,Mean shift:a robust approach toward feature space analysis,IEEE T-PAMI 24(5)(2002)603-619.
[16] S.C.Zhu,A.Yuille,Region competition:unifying snakes,region growing,and Bayes/mdl for multiband image segmentation,IEEE Trans.Pattern Anal.Mach. Intell.18(9)(1996)884-900.
[17] A.K.Jain,M.N.Murty.PJ.Flynn,Data clustering:a review,ACM comput.sur.(CSUR)31(3)(1999)264-323.
[18] R.Adams,L.Bischof,Seeded region growing.IEEE Trans.Pattern Anal.Mach. Intell.16(6)(1994)641-647.
[19] K.Haris,S.N.Efstratiadis,N.Maglaveras,A.K.Katsaggelos,Hybrid image segmentation using watersheds and fast region merging,IEEE Trans.Image Process.7(12)(1998)1684-1699.
[20] A.K.Jain,F.Farrokhnia,Unsupervised texture segmentation using Gabor filters, Pattern Recognit.24(12)(1991)1167-1186.
[21] I.Liu,Y.H.Yang,Multiresolution color image segmentation,IEEE Trans.Pattern Anal.Mach.Intell.16(7)(1994)689-700.
[22] C.Grigorescu,N.Petkov,M.A.Westenberg,Contour detection based on nonclassical receptive field inhibition,IEEE TIP 12(7)(2003)729-739.
[23] G.Papari,N.Petkov,P.Campisi,Artistic edge and corner enhancing smoothing, IEEE TIP 29(10)(2007)2449-2462.
[24] P.Saint-Marc,J.S.Chen,G.Medioni,Adaptive smoothing:a general tool for early vision，IEEE T-PAMI 13(6)(1991)514-529.
[25] C.Tomasi,R.Manduchi,Bilateral filtering for gray and color images,Proceedings of the Sixth International Conference on Computer Vision,Narosa Publishing House,Bombay,1998,p.839.
[26] Mark A.Schulze,John A.Pearce,A morphology-based filter structure for edge-enhancing smoothing.ICIP,vol.2,1994,pp.530-534.
[27] R.van den Boomgaard,Decomposition of the Kuwahara-Nagao operator in terms of linear smoothing and morphological sharpening,Proc.of the 6th International Symposium on Mathematica Morphology,2002, pp.283-292.
[28] I.Pitas,A.N.Venetsanopoulos,Order statistics in digital image processing,Proc. IEEE80(12)(December 1992)1893-1921.
[29] D.Barash,D.Comaniciu,A common framework for nonlinear diffusion,adaptive smoothing,bilateral filtering and mean shift,IVC22(1)(2004)73-81.
[30] P.Bakker,LJ.van Vliet,P.W.Verbeek,Edge preserving orientation adaptive filtering,Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Los Alamitos,1999,pp.535-540,(IEEE).
[31] R.C.Hardie,C.Boncelet,Lum filters:a class of rank-order-based filters for smoothing and sharpening,IEEE TSP 41(3)(1993)1061-1076.
[32] V.1.Ponomaryov,FJ.Galleros-Funes,A.Rosales-Silva,Real-time color imaging basedon rm-filters for impulsive noise reduction,J.Imag.Sci.Tech.49(3)(2005)205-219.
[33] V.Barnett,The ordering of multivariate data,J.Royal Stat.Soc.A 139(3)(1976) 318-355.
[34] K.N.Plataniotis,A.N.Venetsanopoulos,Color lmage Processing and Applications, Springer,2000.
[35] J.T.Astola,P.Haavisto,Y.Neuvo,Vector median filters,Proc.IEEE 78(1990)678-689.
[36] A.Brook,R.Kimmel,N.A.Sochen,Variational restoration and edge detection for color images,J.Math.Imag.Vis.18(3)(2003)247-268.
[37] J.F.Aujol,A.Chambolle,Dual norms and image decomposition models,JCV 63(1)(2005)85-104.
[38] D.Ceman,G.Reynolds,Constrained restoration and the recovery of discontinuities,IEEE T-PAMI 14(3)(1992)367-383.
[39] S.Teboul,LBlanc-Feraud,G.Aubert,M.Barlaud,Variational approach for edge-preserving regularization using coupled pdes,IEEE TIP 7(3)(1998)387-397.
[40] P.C.Hansen,Analysis of discrete ill-posed problems by means of the I-curve, SIAM Rev.34(4)(1992)561-580.
[41] C.R.Vogel,M.E.Oman,Fast,robust total variation-based reconstruction of noisy.blurred images,IEEE TIP 7(6)(1998)813-824.
[42] LI.Rudin,SJ.Osher,E.Fatemi,Nonlinear total variation based noise removal algorithms,Phys.D60(1992)259-268.
[43] A.Chambolle,P.LLions,Image recovery via total variation minimization and related problems,Num.Math.76(2)(1997)167-188.
[44] D.Mumford,J.Shah,Optimal approximations by piecewise smooth functions and variational problems,Comm.Pure Appl.Math.XLll(5)(1988)577-685.
[45] P.Blomgren,T.F.Chan,Color tv:total variation methods for restoration of vector-valued images,IEEE TIP 7(3)(1998)304-309.
[46] T.F.Chan,S.Osher,J.Shen,The digital tv filter and nonlinear denoising,IEEE IP 10(2)(2001)231-241.
[47] A.Marquina,S.Osher,Explicit algorithms for a new time dependent model based on level set motion for nonlinear deblurring and noise removal,SIAM J.Sci. Comp.22(2)(March 2000)387-405.
[48] S.Farsiu,M.D.Robinson,M.Elad,P.Milanfar,Fast and robust multiframe super resolution,IEEETIP 13(10)(2004)1327-1344.
[49] David C.Dobson,RV.Curtis,Convergence of an iterative method for total variation denoising,SIAMJ.Num.Anal.34(5)(1997)1779-1791 (October).
[50] V.Caselles,J.M.Morel,G.Sapiro,A.Tannenbaum,Introduction to the special issue on partial differential equations and geometry-driven diffusion in image processing and analysis,IEEE TIP 7(3)(1998)269-273.
[51] MJ.Black,G.Sapiro,D.H.Marimont,D.Heeger,Robust anisotropic diffusion,IEEE TIP7(3)(1998)421-432.
[52] JWeickert,Theoretical foundations of anisotropic diffusion in image processing. IVC 11(1996)221-236.
[53] P.Perona,J.Malik,Scale-space and edge detection using anisotropic diffusion, IEEE T-PAMI,PAMI 12(7)(1990)629-639.
[54] F.Catte,P.LLions,JM.Morel,T.Coll,Image selective smoothing and edge detection by nonlinear diffusion,SIAMJ.Num.Anal.29(1)(February 1992)182-193.
[55] F.Torkamani-Azar,K.E.Tait,Image recovery using the anisotropic diffusion equation,IEEE TIP 5(11)(1996)1573-1578.
[56] M.Nitzberg.T.Shiota,Nonlinear image filtering with edge and corner enhancement,IEEE T-PAMI 14(8)(1992)826-833.
[57] C.Sapiro,A.Tannenbaum,Afine invariant scale-space,UCV 11(1)(1993)25-44.
[58] LAlvarez,LMazorra,Signal and image restoration using shock filters and anisotropic diffusion,SIAMJ Num.Anal.31(2)(April 1994)590-605.
[59] R.T.Whitaker,Geometry-limited diffusion in the characterization of geometric patches in images,CVGIP 57(1)(January 1993)111-120.
[60] G.Sapiro,D.L Ringach,Anisotropic diffusion of multivalued images with applications to color filtering.IEEE TIP 5(11)(1996)1582-1586.
[61] F.L Fontaine,S.Basu,Wavelet-based solution to anisotropic diffusion equation for edge detection,Int.J.Imaging Sys.Tech.9(5)(1999)356-368.
[62] B.M.ter Haar Romeny,Front-end Vision and Multi-scale lmage Analysis,Kluwer Academic Publishers,2002.
[63] D.Marr,E.Hildreth,Theory of edge detection,Proc.Royal Soc.London B207(1167)(1980)187-217.
[64] X.Wang.Laplacian operator-based edge detectors,PAMI,IEEE Trans.29(5)(2007)886-890.
[65] J.Vriendt,Accuracy of the zero crossings of the second directional derivative as an edge detector,Multidim.Sys.Sign.Proc.4(3)(1993)227-251.
[66] LM.Kennedy.M.Basu,Image enhancement using a human visual system model. PR30(12)(1997)2001-2014.
[67] LM.Kennedy,M.Basu,A Gaussian derivative operator for authentic edge detection and accurate edge localization,JPRAI 13(3)(1999)367-380.
[68] J.J.Clark,Singularity theory and phantom edges in scale space,IEEE T-PAMI10(5)(September 1988)720-727.
[69] M.Bertero,T.A.Poggio,V.Torre,ll-posed problems in early vision,Proc.IEEE76 (8)(1988)869-889.
[70] K.Anil,Jain,Fundamentals of Digital lmage Processing.Prentice-Hall,Englewood Cliffs,1989.
[71] LGanesan,P.Bhattacharyya,Edge detection in untextured and textured images a common computational framework,IEEE SMC 27(5)(1997)823-834.
[72] J.F.Canny,A variational approach to edge detection,in:M.A.Genesereth(Ed.).Proceedings of the National Conference on Artificial Intelligence,AAAI Press, Washington,D.C,1983,pp.54-58,(August).
[73] J.F.Canny.A computational approach to edge detection,IEEE T-PAMI 8(6)(1986)679-698.
[74] M.Petrou,J.Kittler,Optimal edge detectors for ramp edges,IEEE T-PAMI 13(5) (1991)483-491.
[75] S.Sarkar,K.LBoyer,On optimal infinite impulse response edge detection filters, IEEE T-PAMI 13(11)(1991)1154-1171.
[76] D.R.Demigny,T.Kamle,A discrete expression of Canny's criteria for step edge detector performances evaluation,IEEE T-PAMI 19(11)(1997)1199-1211.
[77] M.Unser,A.Aldroubi,M.Eden,B-spline signal processing:partI-theory,IEEE TSP 41(2)(1993)821-833.
[78] M.Unser,A.Aldroubi,M.Eden,B-spline signal processing:part IⅡ-efficient design and applications,IEEE TSP 41(2)(1993)834-848.
[79] G.Chen,Y.H.H. Yang,Edge-detection by regularized cubic B-spline fitting,IEEET-SMC 25(4)(1995)636-643.
[80] Y.P.Wang,Image representations using multiscale differential operators,IEEE TIP 8(12)(1999)1757-1771.
[81] B.u,J.Shen,Two-dimensional local moment,surface fitting and their fast computation,PR27(6)(1994)785-790.
[82] S.Ghosal,R.Mehrotra,Detection of composite edges,IEEE TIP 3(1)(1994)14-25.
[83] K.H.Liang.T.Tjahjadi,Y.H.Yang.Roof edge detection using regularized cubic bspline fitting,PR 30(5)(1997)719-728.
[84] K.H.Liang.T.Tjahjadi,Y.H.Yang,Bounded diffusion for multiscale edge detection using regularized cubic b-spline fitting,IEEE SMC29(2)(1999)291-297.
[85] Y.P.Wang,S.L Lee,Scale-space derived from B-splines,IEEE T-PAMI 20(10)(1998)1040-1055.
[86] P.Qiu,Jump surface estimation,edge detection,and image restoration,J.Am. Stat.Ass.102(478)(2007)745-756.
[87]JS.Huang,D.H.Tseng Statistical theory ofedge detection,CGIP 43(1988)337-346.
[88]E.Chuang,D.Sher,xtest for feature detection,PR 26(11)(1993)1671-1681.
[89] D.H.Lim,SJ.Jang,Comparison of two-sample tests for edge detection in noisy images,Stat 51(1)(2002)21-30.
[90] M.A.Ruzon,C.Tomasi,Edge,junction,and corner detection using color distributions,IEEE T-PAMI 23(11)(2001)1281-1295.
[91] Y.Rubner,C.Tomasi,LJ.Guibas,The earth mover's distance as a metric for image retrieval,IJCV 40(2)(2000)99-121.
[92] J.Malik,S.Belongie,T.K.Leung.J.Shi,Contour and texture analysis for image segmentation,JCV 43(1)(2001)7-27.
[93] N.Chaji,H.Ghassemian,Texture-gradient-based contour detection,JASP(2006)(2006).
[94] Mark Nitzberg.David Mumford,Takahiro Shiota,Filtering.Segmentation and Depth,volume 662 of Lecture Notes in Computer Science,Springer, 1993.
[95] S.Ando,Image field categorization and edge/corner detection from gradient covariance,IEEE T-PAMI 22(2)(2000)179-190.
[96] P.H.Gregson,Using angular dispersion of gradient direction for detecting edge ribbons,IEEE T-PAMI 15(7)(1993)682-696.
[97] J.B.Martens,Local orientation analysis in images by means of the hermite transform,IEEE TIP 6(8)(1997)1103-1116.
[98] DJ.Park,Kwon M.Nam,R.H.Park,Edge detection in noisy images based on the co-occurrence matrix,PR 27(6)(1994)765-775.
[99] S.M.Smith,J.M.Brady,Susan:a new approach to low-level image-processing. JCV23(1995)45-78.
[100] A.V.Oppenheim,JS.Lim,The importance of phase in signals,Proc.IEEE 69(5)(1981)529-541.
[101] M.C.Morrone,D.Burr,J.Ross,R.Owens,Mach bands are phase dependent,Nat.(1986)250-253.
[102] M.Morrone,D.Burr,Feature detection in human vision:a phase dependent energy model,Proc.Royal Soc.London Bull.(1988)221-245.
[103] M.Morrone.R.Owens,Feature detection from local energy.PRL 6(1987) 303-313.
[104] P.Kovesi,lmage features from phase congruency,Videre:J.Comp.Vis.Res.1(3) (1999)(26pages).
[105] D.Boukerroui,J.A.Noble,M.Brady,On the choice of band-pass quadrature filters, J.Math.lmag.Vis.21(1)(2004)53-80.
[106] JMarroquin,JE.Figueroa,M.Servin,Robust quadrature filters,J.Opt.Soc.Am. A 14(4)(1997)779-791.
[107] JG.Daugman,Uncertainty relation for resolution in space,spatial frequency,and orientation optimized by two-dimensional visual cortical filters,J.Opt.Soc.Am. A 2(1985)1160-1169.
[108] J.K.Kamarainen,V.Kyrki,H.Kalviainen,Invariance properties of Gabor filter-based features-overview and applications,IEEE TIP 15(5)(2006)1088-1099.
[109] M.Felsberg.G.Sommer,The monogenic signal,IEEE TSP 49(12)(2001) 3136-3144.
[110] P.Perona,J.Malik,Detecting and localizing edges composed of steps,peaks and roofs,International Conference on Computer Vision,1990,pp.52-57.
[111] D.Reisfeld,The constrained phase congruency feature detector:simultaneous localization,classification and scale determination,PRL17(11)(1996)1161-1169.
[112] B.Robbins,R.Owens,2d feature detection via local energy,IVC 15(5)(1997) 353-368.
[113] S.Venkatesh,R.Owens,On the dassification of image features,PRL11(5)(1990) 339-349.
[114] C.Ronse,On idempotence and related requirements in edge detection,IEEE T-PAMI 15(5)(1993)484-491.
[115] M.Kisworo,S.Venkatesh,G.West,Modeling edges at subpixel accuracy using the local energy approach,IEEE T-PAMI 16(4)(1994)405-410.
[116] PLRosin,Edges:saliency measures and automatic thresholding.Mach.Vis. Appl.9(4)(1997)139-159.
[117] J.lee,R.Haralick,L Shapiro,Morphologic edge detection,IEEE JRA 3(2)(1987)142-156.
[118] F.Rivest,P.Soile,S.Beucher,Morphological gradients,J.Elec.lmag.2(4)(1993)326-336.
[119] A.N.Evans,X.liu,A morphological gradient approach to color edge detection, IEEE TIP 15(6)(2006)1454-1463.
[120] P.E.Trahanias,A.N.Venetsanopoulos,Vector order statistics operators as color edge detectors,IEEE SMC 26(1)(1996)135-143.
[121] S.Y.Zhu,K.N.Plataniotis,AN.Venetsanopoulos,Comprehensive analysis of edge detection in color image processing.Opt.Eng.38(1999)612.
[122] Richard Duda,Peter Hart,David Stork,Pattern Ciassification,John Wiley and Sons,2001.
[123] Peter Meer,Bogdan Georgescu,Edge detection with embedded confidence,IEEE T-PAMI 23(12)(2001)1351-1365.
[124] S.Konishi,A.L.Yuille,J.M.Coughlan,S.C.Zhu,Statistical edge detection:learning and evaluating edge cues,IEEE T-PAMI 25(2003)57-74.
[125] D.R.Martin,C.Fowlkes,J.Malik,Learning to detect natural image boundaries using brightness and texture,in:Suzanna Becker,Sebastian Thrun,Klaus Obermaye(Eds.),NIPS,MIT Press,2002,pp.1255-1262.
[126] N.Petkov,M.A.Westenberg,Suppression of contour perception by band-limited noise and its relation to non-classical receptive field inhibition,Biol.Cyb.88(2003)236-246.
[127] TS.Meese,RJ.Summers,DJ.Holmes,S.A.Wallis,Contextual modulation involves suppression and facilitation from the center and the surround,J.Vis.7(4)(2007)7.
[128] C.Grigorescu,N.Petkov,M.A.Westenberg,Contour and boundary detection improved by surround suppression of texture edges,IVC22(8)(2004)609-622.
[129] G.Papari,P.Campisi,N.Petkov,A.Neri,A biologically motivated multiresolution approach to contour detection,JASP(2007)(28 pages).
[130] G.Papari,P.Campisi,N.Petkov,A.Neri,A multiscale approach to contour detection by texture suppression,Proc.of Electronic Imaging,Image proc.:Alg. and Syst，，2006，(60640D-1-60640D-12).
[131] G.Papari,P.Campisi,N.Petkov,Contour detection by multiresolution surround inhibition,Proc.ICIP,2006,pp.749-752.
[132] G.Papari,P.Campisi,N.Petkov,Multilevel surround inhibition:a biologically motivated contour detector,Proc.of Electronic Imaging,Image proc.:Alg.and Syst，，2007，(pages 649702-1-6497-11).
[133] Mi-Suen Lee,Gerard Medioni,Grouping...…into regions,curves,and junctions, CVIU 76(1)(October 1999)54-69.
[134] G.Guy,G.Medioni,Inferring global perceptual contours from local features,JCV 20(1)(1996)113-133.
[135] W.S.Tong,C.K.Tang,Robust estimation of adaptive tensors of curvature by tensor voting,IEEE T-PAMI 27(3)(2005)434-449.
[136] M.Ursino,G.E.La Cara,A model of contextual interactions and contour detection in primary visual cortex,Neural Netw.17(5-6)(2004)719-735.
[137] T.N.Mundhenk,LItti,Computational modeling and exploration of contour integration for visual saliency,Biol.Cyb.93(3)(2005)188-212.
[138] DJ.Field,A.Hayes,R.F.Hess,Contour integration by the human visual system: evidence for a local“association field",Vis.Res.33(2)(1993)173-193.
[139] S.C.Yen,LH.Finkel,Extraction of perceptually salient contours by striate cortical networks,Vis.Res.38(5)(1998)719-741.
[140] Zhaoping Li,A neural model of contour integration in the primary visual cortex, Neur.Comp.10(4)(1998)903-940.
[141] Q.Tang,N.Sang,T.Zhang,Extraction of salient contours from cluttered scenes, PR40(11)(2007)3100-3109.
[142] N.Sang.Q.Tang,T.Zhang,Contour detection based on inhibition of primary visual cortex,JIMW 47(1)(2007).
[143] A.Rosenfeld,R.A.Hummel,S.W.Zucker,Scene labeling by relaxation operations, IEEE T-SMC6(6)(1976)420-433.
[144] JF.Boyce,J.Feng.E.R.Haddow,Relaxation labelling and the entropy of neighbourhood information,PRL 6(4)(1987)225-234.
[145] P.Parent,S.W.Zucker,Trace inference,curvature consistency,and curve detection,IEEE T-PAMI11(8)(1989)823-839.
[146] M.Pelillo,M.Refice,Learning compatibility coefficients for relaxation labeling processes,IEEE Trans.Pattern Anal.Mach.intell.16(9)(1994)933-945.
[147] SZ Li,H.Wang.M.Petrou,Relaxation labeling of Markov random fields, Proceedings of IEEE International Conference on Pattern Recognition,vol.1, 1994,pp.488-492.
[148] S.Geman,D.Geman,Stochastic relaxation,Gibbs distributions and the Bayesian restoration of images,IEEE Trans.Pattern Anal.Mach.Intell.6(6)(1984)721-741.
[149] T.Werner,A linear programming approach to max-sum problem:a review,IEEE Trans.Pattern Anal.Mach.Intell.29(7)(2007)1165-1179.
[150] JKittler,J.llingworth,Relaxation labelling algorithms-a review,Image Vis. Comput.3(4)(1986)206-216.
[151] O.Ben-Shahar,S.W.Zucker.The perceptual organization of texture flow:a contextual inference approach,IEEE T-PAMI 25(4)(2003)401-417.
[152] H.Wang,E.R.Hancock,Probabilistic relaxation labelling using the Fokker-Planck equation,Pattern Recognit.41(11)(2008)3393-3411.
[153] JS.Yedidia,W.T.Freeman,Y.Weiss,Constructing free-energy approximations and generalized belief propagation algorithms,IEEE Trans.Inf.Theory 51(7)(2005)2282-2312.
[154] MJ.Wainwright,TS.Jaakkola,A.S.Willsky,A new class of upper bounds on the log partition function,IEEE Trans.Inf.Theory 51(7)(2005)2313-2335.
[155] MJ.Wainwright,TS.Jaakkola,A.S.Willsky,MAP estimation via agreement on trees: message-passing and linear programming,IEEE Trans.Inf.Theory 51(11)(2005) 3697-3717.
[156] LMatalas,R.Benjamin,R.Kitney,An edge detection technique using the facet modeland parameterized relaxation labeling,IEEE T-PAMI 19(4)(1997) 328-341.
[157] J.H.Elder,R.M.Goldberg.Ecological statistics of Gestalt laws for the perceptual organization of contours,J.Vis.2(4)(2002)324-353.
[158] JS.Stahl,S.Wang,Globally optimal grouping for symmetric boundaries and region information,IEEE Trans.Pattern Anal.Mach.Intel.30(3)(2008)395-411.
[159] A.Amir,M.Lindenbaum,A generic grouping algorithm and its quantitative analysis,IEEE T-PAMI 20(2)(1998)168-185.
[160] LR.Williams,K.K.Thornber,A comparison of measures for detecting natural shapes in cluttered backgrounds,IJCV34(2)(1999)81-96.
[161] A.Sanfeliu,R.Alquezar,J.Andrade,J.Climent,F.Serratosa,J. Verges,Graph-based representations and techniques for image processing and image analysis,PR35 (3)(2002)639-650.
[162] A.D.Sappa,Unsupervised contour closure algorithm for range image edge-based segmentation,IEEE TIP 15(2)(2006)377-384.
[163] X.Ren,C.Fowlkes,J.Malik,Scale-invariant contour completion using conditional random fields,ICCV,IEEE Computer Society,Washington,DCUSA,2005, pp.1214-1221.
[164] S.Mahamud,LR.Williams,K.K.Thornber,K.Xu,Segmentation of multiple salient closed contours from real images,IEEE T-PAMI 25(4)(2003)433-444.
[165] I.Kovacs,B.Julesz,A closed curve is much more than an incomplete one:effect of closure in figure-ground segmentation,PNAS 90(16)(1993)7495-7497.
[166] J.Elder,S.Zucker,A measure of closure,Vis.Res.34(24)(1994)3361-3370.
[167] S.Casadei,S.Mitter,Beyond the uniqueness assumption:ambiguity representation and redundancy elimination in the computation of a covering sample of salient contour cycles,CVIU 76(1)(1999)19-35.
[168] E.Saund,Finding perceptually closed paths in sketches and drawings,IEEET-PAMI 25(4)(2003)475-491.
[169] E.Saund,Perceptual organization of occluding contours of opaque surfaces,CVIU 76(1)(1999)70-82.
[170] D.W.Jacobs,Robust and efficient detection of salient convex groups,IEEE Trans. Pattern Anal.Mach.Intell.18(1)(1996)23-37.
[171] J.H.Elder,S.W.Zucker,Computing contour closure,Lect.Notes Comput.Sci.1064(1996)399-412.
[172] K.K.Thornber,LR.Williams,Analytic solution of stochastic completion fields,Biol.Cybern.75(2)(1996)141-151.
[173] T.H.Cormen,C.E.Leiserson,R.L Rivest,C.Stein,Introduction to Algorithms,2001.
[174] S.Wang.T.Kubota,J.M.Siskind,J.Wang.Salient closed boundary extraction with ratio contour,IEEE T-PAMI 27(4)(2005)546-561.
[175] LLam,S.W.Lee,C.Y.Suen,Thinning methodologies-a comprehensive survey, IEEE Trans.Pattern Anal.Mach.Intell.14(9)(1992)869-885.
[176] H.I.Choi,S.W.Choi,H.P.Moon,Mathematical theory of medial axis transform. Pac.J.Math.181(1)(1997)57-88.
[177] H.Shroff.J.Ben-Arie,Finding shape axes using magnetic fields,IEEE Trans.Image Process.8(10)(1999)1388-1394.
[178] K.Siddiqi,S.Bouix,A.Tannenbaum,S.W.Zucker,Hamilton-Jacobi skeletons,Int.1.Comput.Vision 48(3)(2002)215-231.
[179] X.Bai,LJ.Latecki,W.Y.Liu,Skeleton pruning by contour partitioning with discrete curve evolution,IEEE Trans.Pattern Anal.Mach.Intell.29(3)(2007)449-462.
[180] R.Mohan,R.Nevatia,Perceptual organization for scene segmentation and description,IEEE Trans.Pattern Anal.Mach.Intell.14(6)(1992)616-635.
[181] T.Tuytelaars,A.Turina,L Van Gool,Noncombinatorial detection of regular repetitions under perspective skew,IEEE Trans.Pattern Anal.Mach.Intell.25(4)(2003)418-432.
[182] H.Cornelius,G.Loy,Detecting bilateral symmetry in perspective,Workshop on Perceptual Organization in Computer Vision,2006,pp.191-198.
[183] X.Jiang.An adaptive contour closure algorithm and its experimental evaluation. IEEE T-PAMI 22(11)(2000)1252-1265.
[184] G.Papari,N.Petkov,Adaptive pseudo dilation for Gestalt edge grouping and contour detection,IEEE Trans.Image Process.17(10)(2008)1950-1962.
[185] PF.M.Nacken,A metric for line segments,IEEE T-PAMI 15(12)(1993)1312-1318.
[186] A.M.Marti' nez,P.Mittrapiyanuruk,A.C.Kak,On combining graph-partitioning with non-parametric clustering for image segmentation,CVIU 95(1)(2004)72-85.
[187] E.Engbers,A.W.M.Smeulders,Design considerations for generic grouping in vision,IEEE T-PAMI 25(4)(2003)445-457.
[188] M.Kass,A.Witkin,D.Terzopoulos,Snakes:active contour models,JCV 1(4)(1987)321-331.
[189] V.Caselles,R.Kimmel,G.Sapiro,Geodesic active contours,JCV 22(1)(1997) 61-79.
[190] S.Osher,J.Sethian,Fronts propagating with curvature-dependent speed-algorithms based on Hamilton-Jacobi formulations,J.Comp.Phys.79(1)(1988)12-49.
[191] T.O.C.View,A topology preserving level set method for geometric deformable models,IEEE T-PAMI 25(6)(2003)755-768.
[192] G.Sundaramoorthi,A.Yezzi,Global regularizing flows with topology preservation for active contours and polygons,IEEE TIP 16(3)(2007)803-812.
[193] S.Osher,R.P.Fedkiw,Level set methods-an overview and some recent results, J.Comp.Phys.169(2)(2001)463-502.
[194] LH.Staib,J.5.Duncan,Boundary finding with parametrically deformable models, IEEE T-PAMI 14(11)(1992)1061-1075.
[195] LD.Cohen,I.Cohen,Finite-element methods for active contour models and balloons for 2-d and 3-d images,IEEE T-PAMI 15(11)(1993)1131-1147.
[196] S.R.Gunn,M.S.Nixon,A robust snake implementation;a dual active contour, IEEE T-PAMI 19(1)(1997)63-68.
[197] H.Yan,Fuzzy curve-tracing algorithm,IEEE SMC 31(5)(2001)768-780.
[198] H.Yan,Convergence condition and efficient implementation of the fuzzy curve-tracing(fct)algorithm,IEEE SMC 34(1)(2004)210-221.
[199] D.Geiger,A.Gupta,LA.Costa,J.Vlontzos,Dynamic programming for detecting, tracking,and matching deformable contours,IEEE T-PAMI 17(3)(1995) 294-302.
[200] A.C.Jalba,M.H.F.Wilkinson,J.Roerdink,Cpm:a deformable model for shape recovery and segmentation based on charged particles,IEEE T-PAMI 26(10)(2004)1320-1335.
[201] H.W.Park,T.Schoepflin,Y.Kim,Active contour model with gradient directional information:directional snake,IEEE TRANS.Circ.Sys.Video Tech.11(2)(2001) 252-256.
[202] A.Dumitras,A.N.Venetsanopoulos,Angular map-driven snakes with application to object shape description in color images,IEEE TIP 10(12)(2001)1851-1859.
[203] S.Liang.T.Mclnerney,D.Terzopoulos,United snakes.Med.Im.Anal.10(2)(2006)215-233.
[204] A.Blake,M.Isard,Active Contours:The Application of Techniques from Graphics, Vision,Control Theory and Statistics to Visual Tracking of Shapes in Motion, Springer-Verlag,New York,1998(Inc.Secaucus,NJ,USA).
[205] J5.Suri,K.Liu,S.Singh,S.N.Laxminarayan,X.Zeng,L Reden,Shape recovery algorithms using level sets in 2-d/3-d medical imagery:a state-of-the-art review,IEEE ITB 6(1)(2002)8-28.
[206] C.Xu,J.LPrince,Snakes,shapes,and gradient vector flow,IEEE TIP 7(3)(1998) 359-369.
[207] N.Paragios,O.Mellina-Gottardo,V.Ramesh,Gradient vector flow fast geometric active contours,IEEE T-PAMI 26(3)(2004)402-407.
[208] M.LSakalli,K.M.H.Yan,A faster converging snake algorithm to locate object boundaries,IEEE TIP 15(5)(2006)1182-1191.
[209] X.M.Pardo,D.Cabello,Biomedical active segmentation guided by edge saliency. PRL 21(6-7)(2000)559-572.
[210] R.Ronfard,Region-based strategies for active contour models,JCV 13(2)(1994) 229-251.
[211] T.F.Chan,LAVese,Active contours without edges,IEEE TIP 10(2)(2001)266-277.
[212] H.Li,AJ.Yezzi,Local or global minima:flexible dual-front active contours,IEEE T-PAMI 29(1)(2007)1-14.
[213] N.Paragios,R.Deriche,Geodesic active regions and level set methods for supervised texture segmentation,IJCV 46(3)(2002)223-247.
[214] LA.Vese,T.F.Chan,A multiphase level set framework for image segmentation using the Mumford and Shah model,JCV 50(3)(2002)271-293.
[215] T.Chan,B.Sandberg,L Vese,Active contours without edges for vector-valued images,J.Vis.Comm.Image Repr.11(2)(2000)130-131.
[216] M.E.Leventon,W.E.L Grimson,O.D.Faugeras,Statistical shape influence in geodesic active contours,CVPR,2000,pp.316-323.
[217] A.Tsai,A.Yezzi Jr,W.Wells,C.Tempany,D.Tucker,A.Fan, W.E.Grimson,A. Willsky,A shape-based approach to the segmentation of medical imagery using level sets,IEEE TMI 22(2)(2003)137-154.
[218] J.A.Sethian,Level Set Methods,Cambridge University Press,1996.
[219] D.Cremers,F.Tischhauser,J.Weickert,C.Schnorr,Diffusion snakes:introducing statistical shape knowledge into the Mumford-Shah functional,JCV 50(3)(2002)295-313.
[220] D.Cremers,T.Kohlberger,C.Schnorr,Shape statistics in kernel space for variational image segmentation,PR 36(9)(2003)1929-1943.
[221] X.Bresson,P.Vandergheynst,J.P.Thiran,A variational model for object segmentation using boundary information and shape prior driven by the Mumford-Shah functional,JCV 68(2)(2006)145-162.
[222] A.Kostin,JKittler,W.Christmas,Object recognition by symmetrised graph matching using relaxation labelling with an inhibitory mechanism,Pattern Recognit.Lett.26(3)(2005)381-393.
[223] F.M.Ansia,M.G.Penedo,C.Marino,A.Mosquera,J.Lopez,Automatic 3D shape reconstruction of bones using active net based segmentation, International Conference on Pattern Recognition,2000,pp.486-489.
[224] JJ.Koenderink,The structure of images,Biol.Cyb.50(1984)363-370.
[225] S.G.Mallat,Multifrequency channel decomposition of images and wavelet models,IEEE Trans.Acoust.Speech,Signal Proces.37(12)(1989)2091-2110.
[226] J.H.Elder,S.W.Zucker,Local scale control for edge detection and blur estimation, IEEE T-PAMI 20(7)(1998)699-716.
[227] S.G.Mallat,A theory for multiresolution signal decomposition:the wavelet representation,IEEE T-PAMI 11(7)(1989)674-693.
[228] LDaubechies,The wavelet transform,time-frequency localization and signal analysis,IEEE TIT 36(5)(1990)961-1005.
[229] D.L Donoho,LM.Johnstone,ideal spatial adaptation via wavelet shrinkage, Biom.81(s 425)(1992)425-455.
[230] A.LYuille,T.A.Poggio,Scaling theorems for zero crossings,IEEE T-PAMI 8(1) (1986)15-25.
[231] j.Babaud,A.P.Witkin,M.Baudin,R.O.Duda,Uniqueness of the Gaussian kernel for scale-space filtering,IEEE T-PAMI 8(1)(1986)26-33.
[232] LAlvarez,F.Guichard,P.LLions,J.M.Morel,Axioms and fundamental equations of image processing,Arch.Rat.Mech.Anal.123(3)(1993)199-257.
[233] J.Weickert,S.Ishikawa,A.Imiya,Linear scale-space has first been proposed in Japan,J.Math.Imag.Vis.10(3)(1999)237-252.
[234] E.J.Pauwels,LJ.van Gool,P.Fiddelaers,T.Moons,An extended class of scale-invariant and recursive scale space filters,IEEE T-PAMI 17(7)(1995)691-701.
[235] R.Duits,LFlorack,J.de Graaf,B.ter Haar Romeny,On the axioms of scale space theory,J.Math.lmag.Vis.20(3)(2004)267-298.
[236] M.Felisberg.G.Sommer,The monogenic scale-space:a unifying approach to phase-based image processing in scale-space,J.Math.Imag.Vis.21(1)(2004)5-26.
[237] M.Felsberg,R.Duits,L Florack,The monogenic scale space on a rectangular domain and its features,IJCV 64(2)(2005)187-201.
[238] Bernhard Burgeth,Stephan Didas,Joachim Weickert,The Bessel scale-space,DSSCV, volume 3753 of lecture Notes in Computer Science,Springer,2005,pp.84-95.
[239] B.Burgeth,S.Didas,JWeickert,Relativistic scale-spaces,Scale Space,2005,pp.1-12.
[240] R.Duits,M.Felsberg,LMJ.Florack,B.Platel,Alpha scale spaces on a bounded domain,scale space,2003,pp.494-510.
[241] Remco Duits,Frans Kanters,Luc Florack,M.Bart,ter Haar Romeny,A comparison of the deep structure of alpha-scale spaces,DSSCV,volume 3753 of Lecture Notes in Computer Science,Springer,2005,pp.234-248.
[242] D.Marr,Vision,Freeman,San Francisco,1982.
[243] G.Steidl,J.Weickert,T.Brox,P.Mrazek,M.Welk,On the equivalence of soft wavelet shrinkage,total variation diffusion,total variation regularization,and SIDEs,SIAM J.Num.Anal.42(2)(April 2004)686-713.
[244] JXu,S.Osher,Iterative regularization and nonlinear inverse scale space applied to wavelet-based denoising,IEEE TIP 16(2)(2007)534-544.
[245] M.Nielsen,LFlorack,R.Deriche,Regularization,scale-space,and edge detection filters,J.Math.Imag.Vis.7(4)(1997)291-307.
[246] R.van den Boomgaard,A.Smeulders,The morphological structure of images: the differential equations of morphological scale-space,IEEE T-PAMI 16(11)(1994) 1101-1113.
[247] P.T.Jackway,M.Deriche,Scale-space properties of the multiscale morphological dilation-erosion,IEEE T-PAMI 18(1)(1996)38-51.
[248] A.H.Salden,J.Weickert,B.M.t.H Romenij,Bluman and Kumei's nonlinear scale-space theory,Technical Report,ERCIM-02/99-R067,1999.
[249] A.Chambolle,R.A.DeVore,N.Lee,BJ.Lucier,Nonlinear wavelet image processing:variational problems,compression,and noise removal through wavelet shrinkage,IEEE TIP 7(3)(1998)319.
[250] B.Vidakovic,Nonlinear wavelet shrinkage with Bayes rules and Bayes factors, J.Amer.Stat.Ass.93(441)(1998).
[251] A.Chambolle,B.J.Lucier,Interpreting translation-invariant wavelet shrinkage as a new image smoothing scale space,IEEE TIP 10(7)(2001)993-1000.
[252] B.M.ter Haar Romeny,Geometry-Driven Diffusion in Computer Vision,Kluwer, September,1994.
[253] Joachim Weickert,A review of nonlinear diffusion filtering,in:B.ter Haar Romney,LFlorack,J.Koenderink,M .Viergever(Eds.), Scale-Space Theory in Computer Vision,1252,Springer-Verlag,1997,pp.3-28.
[254] A.H. Salden,B.M.T.H.Romeny.M.A.Viergever,A dynamic scale-space paradigm. J.Math.Imag.Vis.15(3)(2001)127-168.
[255] Y.Lu,R.C.Jain,Behavior of edges in scale space,IEEE T-PAMI 11(4)(April 1989) 337-356.
[256] LFlorack,B.Ter Haar Romeny.M.Viergever,J.Koenderink,The Gaussian scale-space paradigm and the multiscale local jet,JCV 18(1)(1996)61-75.
[257] F.Bergholm,Edge focusing.IEEE T-PAML,PAMI9(6 (1987)726-741(November).
[258] F.Ulupinar,G.G.Medioni,Refining edges detected by a LoG operator,CVGIU 51(1990)275-298.
[259] T.Lindeberg,Detecting salient blob-like image structures and their scale with a scale-space primal sketch:a method for focus-of-attention,IJCV 11(3)(1993) 283-318.
[260] A.Goshtasby,On edge focusing,IVC 12(4)(1994)247-256.
[261] J.Sun,D.Gu,Y.Chen,S.Zhang.A multiscale edge detection algorithm based on wavelet domain vector hidden Markov tree model,PR 37(7)(2004)1315-1324.
[262] S.V.Raman,S.Sarkar,.L.Boyer,Tissue boundary refinement in magnetic resonance images using contour-based scale space matching.IEEE T-Med. Images 10(2)(1991)109-121.
[263] X.M.Pardo,MJCarreira,A.Mosquera,D.Cabello,A snake for CT image segmentation integrating region and edge information,IVC 19(7)(2001) 461-475.
[264] N.Ray,B.Chanda,J.Das,A fast and flexible multiresolution snake with a definite termination criterion,PR 34(7)(2001)1483-1490.
[265] W.Liu,J.A.Zagzebski,T.Varghese,C.R.Dyer,U.Techavipoo,TJ.Hall, Segmentation of elastographic images using a coarse-to-fine active contour model,Ultras.Med.Biol.32(3)(2006)397-408.
[266] M.Li,P.S.Wu,Pyramid edge detection for color images,Opt.Eng.36(5)(1997) 1431-1437.
[267] F.Sjoberg.F.Bergholm,Extraction of diffuse edges by focusing,PRL7(3)(1988) 181-190.
[268] W.Zhang,F.Bergholm,Multi-scale blur estimation and edge type classification for scene analysis,JCV 24(3)(1997)219-250.
[269] T.Lindeberg,Edge detection and ridge detection with automatic scale selection, JCV 30(2)(November 1998)117-156.
[270] DJ.Park,K.M.Nam,R.H.Park,Multiresolution edge detection techniques,PR28 (2)(1995)211-229.
[271] C.F.Olson,Adaptive-scale filtering and feature detection using range data,IEEE T-PAMI 22(9)(2000)983-991.
[272] M.Heath,S.Sarkar,T.Sanocki,K.W.Bowyer,Comparison of edge detectors,CVIU 69(1)(1998)38-54.
[273] M.D.Heath,S.Sarkar,T.Sanocki,K.W.Bowyer,A robust visual method for assessing the relative performance of edge-detection algorithms,IEEE T-PAMI19(12)(1997)1338-1359.
[274] M.C.Shin,D.B.Goldgof,K.W.Bowyer,S.Nikiforou,Comparison of edge detection algorithms using a structure from motion task,IEEE T-SMC 31(4)(2001)589-601.
[275] LKitchen,A.Rosenfeld,Edge evaluation using local edge coherence,IEEET-SMC 11(9)(1981)597-605.
[276] Q.Zhu,Efficient evaluations of edge connectivity and width uniformity,IVC14(1)(1996)21-34.
[277] R.M.Haralick,Digital step edges from zero crossing of second directional derivatives,IEEE T-PAMI6(1)(1984)58-68.
[278] R.M.Haralick,JS.J.Lee,Context dependent edge detection and evaluation,PR23(1-2)(1990)1-19.
[279] Y.Yitzhaky,E.Peli,A method for objective edge detection evaluation and detector parameter selection,IEEE T-PAMI 25(8)(2003)1027-1033.
[280] Y.T.Zhou,V.Venkateswar,R.Chellappa,Edge detection and linear feature extraction using a 2-d random field model,IEEE T-PAMI 11(1)(1989)84-95.
[281] K.Bowyer,C.Kranenburg.S.Dougherty.Edge detector evaluation using empirical ROC curves,CVIU 84(1)(2001)77-103.
[282] S.Chabrier,H.Laurent,B.Emile,C.Rosenberger,P.Marche,A comparative study of supervised evaluation criteria for image segmentation,“EUSIPCO",2004, pp.1143-1146,(EURASIP).
[283] D.P.Huttenlocher,G.A.Klanderman,WJ.Rucklidge,Comparing images using the Hausdorff distance,IEEE T-PAMI 15(9)(1993)850-863.
[284] C.Odet,B.Belaroussi,H.Benoit-Cattin,Scalable discrepancy measures for segmentation evaluation,ICIP,2002,pp.785-788.
[285] Q.Tang,N.Sang.T.Zhang,Contour detection based on contextual influences,IVC 25(8)(2007)1282-1290.
[286] R.A.Hummel,S.W.Zucker,On the foundation of relaxation labeling process,IEEE T-PAMI 5(3)(1983)267-286.
[287] Daniel Crevier,A probabilistic method for extracting chains of collinear segments,CVIU 76(1)(1999)36-53.
[288] M.H.F.Wilkinson,Optimizing edge detectors for robust automatic threshold selection:coping with edge curvature and noise,Graphical Models and Image Process.60(5)(1998)385-401.
[289] P.V.Henstock,D.M.Chelberg.Automatic gradient threshold determination for edge detection,IEEE Trans.Image Process.5(5)(1996)784-787.
[290] S.Venkatesh,P.Rosin,Dynamic threshold determination by local and global edge evaluation,Graphical Models lmage Process.57(2)(1995)146-160.
[291] Litti,C.Koch,A saliency-based search mechanism for overt and covert shifts of visual attention,Vis.Res.40(10-12)(2000)1489-1506.
[292] M.Rousson,N.Paragios,Prior knowledge,level set representations & visual grouping,Int.J.Comput.Vision 76(3)(2008)231-243.