LeetCode Week3: Different Ways to Add Parentheses、Expression Add Operators

   这一周主要实现的还是Divide-and-Conquer部分的题目，但是有一题也涉及到了深度优先搜索，两道题目分别是Different Ways to Add Parentheses、Expression Add Operators。

一、Different Ways to Add Parentheses

题目描述：Given a string of numbers and operators, return all possible results from computing all the different possible ways to group numbers and operators. The valid operators are +, - and *.

Example 1:
Input: “2-1-1”.

((2-1)-1) = 0
(2-(1-1)) = 2

Output: [0, 2]
Example 2
Input: “2*3-4*5”

(2*(3-(4*5))) = -34
((2*3)-(4*5)) = -14
((2*(3-4))*5) = -10
(2*((3-4)*5)) = -10
(((2*3)-4)*5) = 10

Output: [-34, -14, -10, -10, 10]

分析：利用分治法可以解决这个问题，我们遍历一次数组，每当遍历得到的元素是运算符时，运算符左右两边的数组元素都可以分别进行计算，再利用这个运算符将两边的运算结果整合起来即可。

用 2∗3−4∗5 来举例说明。

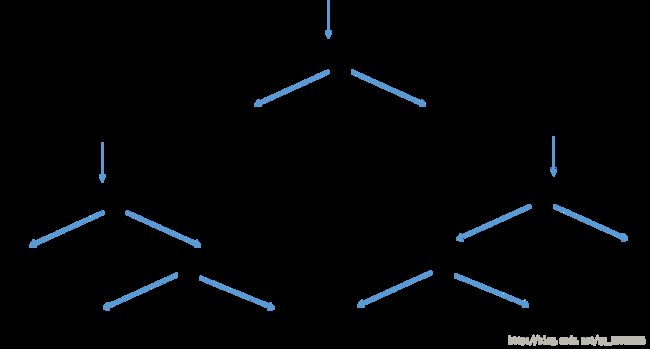
程序从左向右遍历，当遇到第一个“ ∗ ”时，对于这个元素前面的数组元素2和后面的3-4*5，我们可以递归的去计算它们的值，最终再加起来即可。
因为2已经是一个元素了，所以不需要再进行计算，而3-4*5仍然是一个等式，所以我们需要对它进行递归运算。同样对其进行遍历，

• 在遍历到第一个运算符“ − ”时，继续划分数组，如上图左下部分所示，元素3已经不再需要计算；

• 对于4和5，当遍历到“ ∗ ”，就能得到4和5两个单独元素的递归运算，所以到达这一步之后，开始递归上升，分别返回4和5，并利用遍历到的第二个运算符“ ∗ ”进行操作，即可得到20；

• 接着继续递归上升，计算3-20=-17，这样子对于3-4*5，就得到了第一个递归调用的值：-17；

• 这一部分等式继续遍历，即可遍历到第二个运算符“*”，如上图右下部分所示，利用上面的步骤同时可以得到一个返回值-5.

• 等式#-4*5遍历完毕，按照遍历顺序，递归运算后返回的值是(-17,-5)，再利用2乘以这两个元素，就能得到在这一步分治的两个计算结果(-34,-10)，与Example 2的前两个式子的计算一致；

• 继续遍历数组，每遍历到一个运算符就重复上述操作，直到遍历结束。

---

通过这样的过程，就能计算出对于一个等式的多种计算结果。算法的代码过程如下：

class Solution {
public:
    vector<int> diffWaysToCompute(string input) {

        vector<int>result;
        for(int i = 0; i < input.size();i++){
            if(input[i] == '+'||input[i] == '-'||input[i] == '*'){
                vector<int> tmp1 = diffWaysToCompute(input.substr(0,i));
                vector<int> tmp2 = diffWaysToCompute(input.substr(i+1,input.size()));

                int res;
                for(int j = 0; j < tmp1.size();j++)
                    for(int z = 0; z < tmp2.size();z++){
                        res = ((input[i] == '+')?(tmp1[j]+tmp2[z]):((input[i] == '-')?
                                (tmp1[j]-tmp2[z]):(tmp1[j]*tmp2[z])));
                        result.push_back(res);
                    }

                }
        }
        if(result.empty()) result.push_back(atoi(input.c_str()));
        return result;
    }
};

因为一个部分的等式的递归返回并非一个值，所以需要考虑计算顺序。

二、Expression Add Operators

题目描述：Given a string that contains only digits 0-9 and a target value, return all possibilities to add binary operators (not unary) +, -, or * between the digits so they evaluate to the target value.

Example：

“123”, 6 -> [“1+2+3”, “1*2*3”]
“232”, 8 -> [“2*3+2”, “2+3*2”]
“105”, 5 -> [“1*0+5”,”10-5”]
“00”, 0 -> [“0+0”, “0-0”, “0*0”]
“3456237490”,9191 -> []

分析：这个题目最开始拿到的时候我的想法就是每次遍历到一个位置，就把前面的部分和后面的部分分别做递归运算，插入不同的操作符，再来进行两部分的值的运算操作，如下图所示。

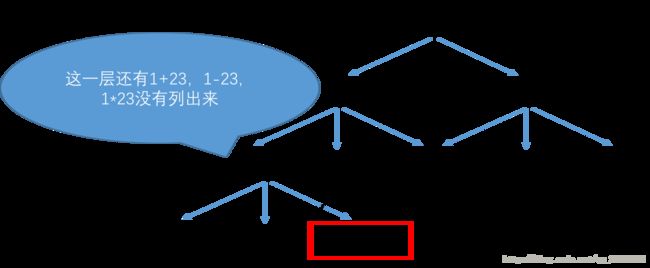
每一次把遍历到一个元素，然后陆续与后面的每个元素做 + ， − 和 ∗ ，但是因为是递归运算，每一次只能执行一种算法操作，那么这个递归过程也是一个深度优先搜索的过程，即对于1，其后面的元素是23，对于1跟2，可以有三种操作，但是一次递归中设定了一种运算操作，那么计算完1+2之后，会继续往后计算1+2+3，1+2-3，1+2*3，才会再来计算1-2，1-2后续的元素计算万之后再计算1*2。

这里存在一个运算符先后级的问题，我们每次在子结点计算得到了一个运算操作序列，下一次加入的序列如果有乘号，那么它的运算优先级会更高，需要先计算乘法，这就需要一个数值上的“回溯”——从1+2计算得到的结果回溯到先计算2*3，再加1。这就表明前一步计算时新加入的元素是2这一信息需要记录下来。

• 考虑curnum是当前的计算结果，prev是前一步中的新加入的元素，如果是加法，那么就是正值，如果是减法，那么就是负值。当下一步加入的操作符是乘法时，从1+2变成1+2*3，curnum = 3，prev = 2，那么加入乘法运算后的结果应该是
  curnum = （3-2）+3*2 = curnum-prev+prev*now；

• 因为乘法的运算优先级较高，如果下一步也需要回溯，2*3需要同时考虑，所以乘法运算后的prev = prev*now；

• 如果只是加法运算，那么prev = now， 减法运算prev = -now（这样回溯的时候就算前面是减法操作1-2*3，因为prev是负值，已经把 − 考虑进去了，所以可以和加法操作相同）。

这里还应该说明，因为运算操作不是局限在0～9的数值，所以还需要考虑，两个数字是否能构成一个十位数，即十位是否不为0。

整个过程的代码如下：

class Solution {
public:
    vector<string>addOperators(string num, int target){
        vector<string>res;
        OperatorsOnSubstr(target,num,0,0,"",res,'*');
        return res;
    }
   /* target: 目标值
   * num: 待处理的字符串
   * curnum: 已经运算得到的数值
   * prev: 前一步运算中新加入的元素
   * prev_oper: 之前运算得到的运算序列串
   * res: 最终的运算结果
   */
    void OperatorsOnSubstr(int target, string num,long long curnum, long long prev,string prev_oper,vector<string>&res,char flag){
        for(int i = 1 ; i <= num.size(); i++){
            string sub1 = num.substr(0,i);
            if (sub1.size() > 1 && sub1[0] =='0') return;
            string sub2 = num.substr(i);

            long long cnt = stoll(sub1);

            if(prev_oper.size() != 0){
                // 乘法递归操作
                OperatorsOnSubstr(target,sub2,(curnum - prev) + prev * cnt,prev * cnt,prev_oper + "*" + sub1, res);
                // 加法递归操作
                OperatorsOnSubStr(target,sub2,curnum+cnt,cnt,prev_oper+"+"+sub1,res); 
                // 减法递归操作
                OperatorsOnSubstr(target,sub2,curnum-cnt,-cnt,prev_oper+"-"+sub1,res);  
            }
            else
                OperatorsOnSubstr(target,sub2,cnt,cnt,sub1,res);
        }
        if(curnum == target && num.size() == 0)
                res.push_back(prev_oper);

    }

};

这里要说明的是，必须使用long类型进行记录，有一个testcase没有过就是因为我用了int类型变量= =