每天一篇论文 370/1000 Consistent Video Depth Estimation
Consistent Video Depth Estimation
作者知乎
本文的一个概念就是稠密深度估计=重建,从重建的角度来做深度估计。
1.摘要
提出了一种重建单目视频中所有像素密集、几何一致性深度估计算法。我们利用传统的structure-from-motion重建来建立视频像素的几何约束。与经典重建中的特殊先验不同,我们使用基于学习的先验,即训练卷积神经网络进行单图像深度估计。在测试时,我们对这个网络进行微调,以满足特定输入视频的几何约束,同时保留其能力来合成视频中约束较少的部分的合理深度细节。通过定量验证,我们的方法比以往的单眼重建方法具有更高的精度和更高的几何一致性。从视觉上看,我们的结果似乎更稳定。我们的算法能够处理具有手持捕获输入视频中等动态场景。改进后的重建质量可应用于多个领域,如场景重建和基于视频的高级视觉效果。
2.基本思想
手持设备拍摄的视频,对于视频中两帧的一个静态点如(桌椅板凳)只要知道相机内参及两帧图像之间的相机运动,就可以在相应的帧上找到一个唯一确定的点。这是理想状态,实际情况是视频通常是用手持的、未经校准的相机拍摄的,所以会出现运动模糊和滚动快门变形,以及糟糕的照明条件可能会增加噪音和额外的模糊。最后,这些视频通常包含动态移动的对象,如人,车和动物,从而打破了许多为静态场景设计的重建系统的核心假设。
本文出发点作者针对
1.不同相机内参不同以及深度估计网络连续帧之间的pose估计不准确造成几何约束不准确,使用COLMAP
2.COLMAP重建的第二个作用是为提供场景的尺度,并且于Learn-based估计的尺度进行匹配
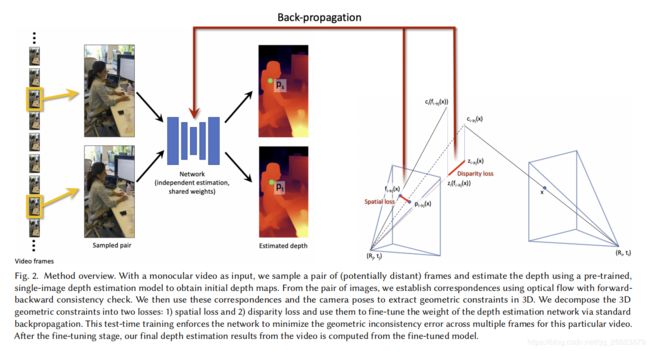
3.Test-time Training:用现有的深度估计网络进行深度估计,通过于几何方法COLMAP重投影得到的几何重投影进行对比,通过几何损失:1)空间损失和2)视差损失,并对误差进行反向传播以更新网络。
4.为了消除场景中人,动物等动态物体,采用Mark-rcnn将其从几何重投影中剔除。
改进通常是显著的,我们最终的深度地图在几何上是一致的,在整个视频中时间上是一致的,同时精确地描绘出清晰的遮挡边界,即使是动态移动的物体。通过计算深度,我们可以得到合适的深度边缘来实现遮挡效果,并使真实场景的几何形状与虚拟物体相互作用。我们展示了各种引人注目的视觉效果,使我们的视频深度估计成为可能
2.方法
2.1 尺度校准(Scale calibration)
因为SFM和learn-based 方法都是基于scale-invariant特性的如下图所示,我的理解:不同尺度下深度估计的结果不会变的。为了使两者比例与几何损失兼容,本文调整SfM比例,因为我们可以简单地通过将所有相机平移乘以一个因子来做到这一点。
D i N N D_i^{NN} DiNN作为深度网络初始的深度图,首先图像 i i i计算相对尺度:
s i = m e d i a n x { D i N N / D i M V S ( x ) ∣ D i M V S ( x ) ≠ 0 } s_i=\underset{x}{median} \{D_i^{NN}/D_i^{MVS}(x)|D_i^{MVS}(x)\neq 0 \} si=xmedian{DiNN/DiMVS(x)∣DiMVS(x)=0}
其中 D ( x ) D(x) D(x)是 x x x的深度值。
进一步计算全局尺度自适应因子 s s s:
s = m e a n x { s i } s= \underset{x}{mean}\{s_i\} s=xmean{si}
然后对于所有的位姿变换的 t i t_i ti,进行尺度调整: t i ∼ = s ⋅ t i \overset{\sim}{t_i}=s\cdot t_i ti∼=s⋅ti
2.2 光流估计
接下来还是得考虑如何让几何投影尽可能的前后一致,对于图像中由于遮挡了一些像素在下一帧中不从在了,这样就破坏了几何投影中的原则。为了考虑运动物体和遮挡/去遮挡(因为它们不满足几何约束或不可靠),应用前向-后向一致性检查,并去除前向-后向误差大于1像素的像素,得到一个二值映射 M i → j M_{i\to j} Mi→j。
2.3 TEST-TIME 训练输入视频
Geometric loss:对于给定视频帧 ( i , j ) (i,j) (i,j)及对应的光流 F i → j F_{i\to j} Fi→j,我们能用用光流测试当前深度估计得一致性,即如果光流估计是准确的,光流位移点 f i → j ( x ) f_{i\to j}(x) fi→j(x)与重投影点 p i → j p_{i\to j} pi→j相同那么深度一定是一致的
网络测试时重新更网络就是根据几何损失 L i → j L_{i\to j} Li→j和反向传播一致性误差损失。
L i → j d i s p a r i t y ( x ) = u i ∣ z i → j − 1 ( x ) − z j − 1 ( f i → j ( x ) ) L_{i \to j}^{disparity}(x)=u_i|z_{i\to j}^{-1}(x) - z_j^{-1}(f_{i \to j}(x)) Li→jdisparity(x)=ui∣zi→j−1(x)−zj−1(fi→j(x))
其中 u i u_i ui是 i i i帧焦距, z i z_i zi和 z i → j z_{i \to j} zi→j分别是 c i c_{i } ci和 c i → j c_{i \to j} ci→j的z标量分量。
这对图像的整体损失只是所有像素点的两种损失的简单组合,其中光流是有效的:
L i → j = 1 ∣ M i → j ∣ ∑ x ∈ M i → j L i → j s p a t i a l ( x ) + λ L i → j d i s p a r i t y ( x ) L_{i \to j}=\frac {1}{|M_{i\to j}|}\sum_{x \in M_{i \to j}} L_{i \to j}^{spatial}(x)+\lambda L_{i \to j}^{disparity}(x) Li→j=∣Mi→j∣1x∈Mi→j∑Li→jspatial(x)+λLi→jdisparity(x)
其中 λ = 0.1 \lambda = 0.1 λ=0.1是平衡系数。
2.4 优化
通过分析第i帧和第j帧之间的几何损失 L i → j L_{i\to j} Li→j,利用标准反向传播对网络权值进行微调。使用预训练的深度估计模型初始化网络参数,使我们能够使用先验知识,在图像上生成可信的深度图,这对传统的基于几何的重构系统是一个挑战。使用固定数量的epoch对网络进行微调(所有实验使用20个epoch)。在实践中,我们发现,通过这个简单的微调步骤,网络训练不会对数据进行过度拟合,因为它不会丧失在场景的无约束或弱约束部分合成合理深度的能力。
2.5 实现细节
试验了几种单目深度估计体系结构和预先训练的权重Mondepth2 和 Neural RGB→D Sensing: Depth and Uncertainty from a Video Camera作为先验训练完成网络。在我们所有的实验中,我们使用ADAM optimizer对网络进行了20个epoch的Test-train,批处理大小为4,学习速率为0.0004。不同长度的视频的测试时间不同。对于一个244帧的视频,在4台NVIDIA Tesla M40 gpu上训练需要40分钟。