剑指offer | 数组问题汇总

1 前言

2 题目

2.1 调整数组顺序使奇数位于偶数前面

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分，并保证奇数和奇数，偶数和偶数之间的相对位置不变。

2.1.1 思路1

思路：

• 遍历所有元素 然后用两个空list分别存取奇数和偶数！
• 最后拼接两个list 奇数在前面！

2.1.2 代码1

# -*- coding:utf-8 -*-
class Solution:
    def reOrderArray(self, array):
        # write code here
        alist = [] # 存取奇数
        blist = [] # 存取偶数
        for i in array:
            if i%2 == 0:
                # 表明为偶数
                blist.append(i)
            else:
                # 表明为奇数
                alist.append(i)
        return alist + blist

2.1.3 思路2

只用一个list实现！

• 即遇到奇数在list前面插入insert
• 遇到偶数在list后面append

2.1.4 代码2

# -*- coding:utf-8 -*-
class Solution:
    def reOrderArray(self, array):
        # write code here
        res = []
        l = len(array)
        for i in range(l):
            if array[l-i-1] % 2 != 0:
                res.insert(0,array[-i-1])
            if array[i] % 2 == 0:
                res.append(array[i])
        return res

2.2 数组中出现次数超过一半的数字

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。

2.2.1 思路1

思路：

• 首先求出数组长度
• 其次统计每个数字出现的次数！昨天好像有一个方法实现了！回去看一下！想起来了！直接使用count函数+ filter函数

2.2.2 代码1

# -*- coding:utf-8 -*-
class Solution:
    def MoreThanHalfNum_Solution(self, numbers):
        # write code here
        # 列表长度
        n = len(numbers) / 2
        a = list(set(list(filter(lambda x: numbers.count(x) > n, numbers))))
        if len(a) == 0:
            return 0
        else:
            return a[0]

2.2.3 思路2

先排序！

• 使用快速排序！然后如果某一个数字的出现次数大于数组一半的长度，那么中间的数肯定就是它了！
• 然后统计中间数出现了多少次！大于一半则ok！
• 注意考虑边界情况！只有一个元素的list！
• 快排时间复杂度为$O(NlogN)$

2.2.4 代码2

class Solution:
    
    def quick_sort(self, alist, first, last):
        # 快排
        if first >= last:
            return 
        
        # 定义两个游标+中值
        low = first
        high = last
        mid = alist[first]
        
        while low < high:
            while alist[high] >= mid and high > low:
                high -= 1
            alist[low] = alist[high]
            
            while alist[low] < mid and low < high:
                low += 1
            alist[high] = alist[low]
        
        alist[low] = mid
        
        # 递归
        self.quick_sort(alist, first, low-1)
        self.quick_sort(alist, low+1, last)
        
        return alist
        
    def MoreThanHalfNum_Solution(self, numbers):
        # write code here
        # 考虑特殊情况
        if len(numbers) == 1:
            return numbers[0]
        # 首先快速排序
        alist = self.quick_sort(numbers, 0, len(numbers)-1)
        print(alist)
        # 判断-看中值出现的次数是否大于一半！因为如果有 肯定中值为出现最多的之一！否则不可能！
        n = int(len(alist)/2)
        # 中值为：
        mid = alist[n]
        # 看有多少个中值！
        count = 0
        for j in alist:
            if j == mid:
                count += 1
        if count > len(alist)/2 :
            return mid
        else:
            return 0

2.3 连续子数组的最大和

HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组，返回它的最大连续子序列的和，你会不会被他忽悠住？(子向量的长度至少是1)

2.3.1 思路1

• 如何考虑呢？
• 肯定没法暴力去搜索啊，因为组合太多了，肯定搞不过来的！那有没有简单的方法呢？判断正负号？或者说有什么规律或者结论？真想不到！

一个牛逼的思路：

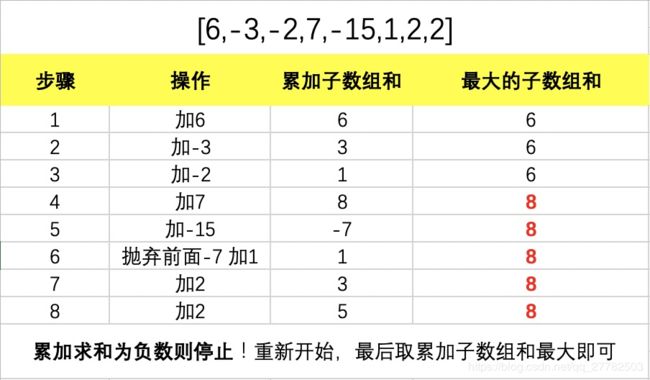
即遇到求和为负数则重新规整为0开始！如果一开始就是负数也添加到全局list中，以防全部为负数！（特殊情况）

2.3.2 代码1

# -*- coding:utf-8 -*-
class Solution:
    def FindGreatestSumOfSubArray(self, array):
        # write code here
        # 法1 找到了规律！
        n = len(array)
        if n==1:
            return array[0]
        
        res = []
        s = 0
        for i in array:
            s += i
            if s > 0:
                # 如果累加和大于0 append到res 继续
                res.append(s)
            else:
                # 如果累加和小于0 s归为0 重新开始 并添加到res
                res.append(s)
                s = 0
        return max(res)

2.3.3 思路2

每一步求和 然后和之前的和取max！！！哇 这个思路牛逼啊！但是有一个问题！怎么断掉前面累加和为负数的情况呢！使用动态规划：

以$array=[1,-2,3,10,-4,7,2,-5]$为例：

首先定义相关符号：

• $F(i)$：以$array[i]$为末尾元素的子数组的和的最大值，子数组的元素的相对位置不变

• $F(i)=max(F(i-1)+array[i]，array[i])$

• $res$：所有子数组的和的最大值

• $res=max(res，F(i))$

开始迭代进行：

• 第一步，$F(0)=max(F(0)+array[0],array[0])=1$，$res=max(res，F(0))=1$
• 第二步，$F(1)=max(F(0)+array[1],array[1])=max(1-2,-2)=-1$，$res=max(res，F(1))=1$
• 第三步，$F(2)=max(F(1)+array[2],array[2])=max(-1+3,3)=3$，$res=max(res，F(2))=3$ 这一步就能有效的实现断掉前面累加和为负数的情况！也是为什么也要把最近的一个数也作为比较的对象，比较的就是前面所有的累加和！
• 第四步，$F(3)=max(F(2)+array[3],array[3])=max(3+10,10)=13$，$res=max(res，F(3))=13$
• 第五步，$F(4)=max(F(3)+array[4],array[4])=max(13-4,-4)=9$，$res=max(res，F(4))=13$
• 第六步，$F(5)=max(F(4)+array[5],array[5])=max(9+7,7)=16$，$res=max(res，F(4))=16$
• 第七步，$F(6)=max(F(5)+array[6],array[6])=max(16+2,2)=18$，$res=max(res，F(5))=18$
• 第八步，$F(7)=max(F(6)+array[7],array[7])=max(18-5,-5)=13$，$res=max(res，F(6))=18$

综上！最大的子数组和为18！

2.3.4 代码2

开始结合上面思路写代码：

# -*- coding:utf-8 -*-
class Solution:
    def FindGreatestSumOfSubArray(self, array):
        # write code here
        # 法1 找到了规律！
        n = len(array)
        if n==1:
            return array[0]
        
        s = 0
        l = 0
        res = float("-inf") # 不能取为0 因为可能全为负数！这样就会出现bug
        for i in array:
            # l为中间过渡变量 表示递归的前n项最大和
            l = s+i
            # s为前多少项和 和 最近一个值的最大值！
            s = max(l, i)
            res = max(res,s)
        return res

2.4 把数组排成最小的数

输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。

2.4.1 思路

• 拼接数字！还是看这个数字的个数位 十位的一个情况！多个数字比较深度！
• 但落实到代码层面怎么去考虑呢？不知道 有点懵逼啊！能不能暴力搜索一下？n的阶乘种排列方式！太复杂了！

牛逼的思路：

• 将每个数字都变成字符串！然后将字符串进行拼接成不同的数 然后再直接取字符串最小的！输出对应的值即可！

2.4.2 代码

# -*- coding:utf-8 -*-
class Solution:
    def PrintMinNumber(self, numbers):
        # write code here
        if len(numbers) == 0:
            return ''
        compare = lambda a, b:cmp(str(a) + str(b), str(b) + str(a))
        min_string = sorted(numbers, cmp = compare)
        return ''.join(str(s) for s in min_string)

2.5 数组中的逆序对

2.5.1 题目

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

2.5.2 思路1

直接暴力搜！

• 首先两两比较值的大小，求和逆序对总数P

2.5.3 代码1

# -*- coding:utf-8 -*-
class Solution:
    def InversePairs(self, data):
        # write code here
        # 暴力搜索
        n = len(data)
        count = 0
        for i in range(n):
            for j in range(i+1,n):
                if data[i] > data[j]:
                    count += 1
        return count%1000000007

思路简单，代码也简单，但是时间复杂度无法通过，为平方复杂度！想办法优化！

2.5.4 思路2

太炫的思路了。

结论：逆序对的总数 = 左边数组中的逆序对的数量 + 右边数组中逆序对的数量 + 左右结合成新的顺序数组时（注意：左右先进行升序排列！）中出现的逆序对的数量

为什么呢？其实也很简单！

• 首先分成两部分没问题，分别统计左右两边数组逆序对的数量
• 现在需要合并！但合并之后需要先对左右两边进行排序！因为防止左右两边内部再加一次！
• 所以就是归并排序的思想！分治法！
• 但代码还是有点难度的~

2.5.5 代码2

# -*- coding:utf-8 -*-
class Solution:
    def InversePairs(self, data):
        # write code here
        if not data:
            return 0
        temp = [i for i in data]
        return self.mergeSort(temp, data, 0, len(data)-1) % 1000000007
       
    def mergeSort(self, temp, data, low, high):
        if low >= high:
            temp[low] = data[low]
            return 0
        mid = (low + high) / 2
        left = self.mergeSort(data, temp, low, mid)
        right = self.mergeSort(data, temp, mid+1, high)
           
        count = 0
        i = low
        j = mid+1
        index = low
        while i <= mid and j <= high:
            if data[i] <= data[j]:
                temp[index] = data[i]
                i += 1
            else:
                temp[index] = data[j]
                count += mid-i+1
                j += 1
            index += 1
        while i <= mid:
            temp[index] = data[i]
            i += 1
            index += 1
        while j <= high:
            temp[index] = data[j]
            j += 1
            index += 1
        return count + left + right

2.6 数字在排序数组中出现的次数

2.6.1 题目

统计一个数字在排序数组中出现的次数。

2.6.2 思路1

• 直接循环遍历判断
• 但加上一个条件 如果位置i等于一个值 但位置i+1不等于 那么就break 因为数组是排序好的！

2.6.3 代码1

# -*- coding:utf-8 -*-
class Solution:
    def GetNumberOfK(self, data, k):
        # write code here
        # 使用简单的方法 循环遍历
        cnt = 0
        for i in range(len(data)):
            if data[i] == k:
                cnt += 1
            elif data[i] == k and data[i+1] != k:
                break
            else:
                continue
        return cnt

2.6.4 思路2

• 二分查找！这样的复杂度会比上面的低，上面的复杂度为O(n)
• 首先通过二分查找找到该元素 然后再以该元素为中心分别向两边去扩散！去找 看有多少相同的！

2.6.5 代码2

遇到的坑：

• 首先是二分查找得需要非递归版本 这样才能返回该找到的元素的位置
• 注意考虑边界条件，即这个元素可能不存在！所以要先写一个判断！
• 注意将mid进行回归！矫正到中值的位置！

# -*- coding:utf-8 -*-
class Solution:
    
    def Binary_search(self, data, k):
        # 二分查找
        n = len(data)-1
        start = 0
        end = n
        
        while start <= end:
            mid = (start + end) // 2
            if data[mid] < k:
                # right
                start = mid + 1
            elif data[mid] > k:
                # left
                end = mid - 1
            else:
                return mid
        return -1
        
    def GetNumberOfK(self, data, k):
        # write code here
        # 使用二分查找
        mid = self.Binary_search(data, k)
        if mid == -1:
            return 0
        else:
            cnt = 1

            while mid + 1 <= len(data)-1 and data[mid+1] == k:
                # 防止越界 + 符合条件
                mid += 1
                cnt += 1

            mid_org = mid - cnt + 1
            while mid_org - 1 >= 0 and data[mid_org - 1] == k:
                # 防止越界 + 符合条件
                mid_org -= 1
                cnt += 1

            return cnt

2.7 数组中只出现一次的数字

2.7.1 题目

一个整型数组里除了两个数字之外，其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。

2.7.2 思路1

• 暴力解法！直接遍历！
• 结果存入到字典！最后遍历字典即可！
• 注意下标！！！
• 以及注意字典判断某个key是否存在的方法

2.7.3 代码1

# -*- coding:utf-8 -*-
class Solution:
    # 返回[a,b] 其中ab是出现一次的两个数字
    def FindNumsAppearOnce(self, array):
        # write code here
        res = []
        dic = {}
        for i in range(len(array)):
            #if array[i] in dic:
            if array[i] in dic:
                dic[array[i]] += 1
            else:
                dic[array[i]] = 0
        for k,v in dic.items():
            if v == 0:
                res.append(k)
        return res

2.7.4 思路2

• 先排序！然后统计 如果次数为1
• 好像不太行的！！！
• 用的异或的思路！但是代码太复杂了！忽略！

2.8 数组中重复的数字

2.8.1 题目

在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如，如果输入长度为7的数组{2,3,1,0,2,5,3}，那么对应的输出是第一个重复的数字2。

2.8.2 思路1

• 遍历！用一个字典来判断！key为值 value为出现的次数
• 如果最后次数大于1则break！
• 记得加一个cnt来判断是否进入了某一个循环！

2.8.3 代码1

# -*- coding:utf-8 -*-
class Solution:
    # 这里要特别注意~找到任意重复的一个值并赋值到duplication[0]
    # 函数返回True/False
    def duplicate(self, numbers, duplication):
        # write code here
        dic = {}
        cnt = 0 
        for num in numbers:
            if num in dic:
                dic[num] += 1
                if dic[num] == 2:
                    cnt += 1
                    duplication[0] = num
                    break
                else:
                    continue
            else:
                dic[num]=1
        if cnt != 0:
            return True
        else:
            return False

2.9 构建乘积数组

2.9.1 题目描述

给定一个数组A[0,1,…,n-1],请构建一个数组B[0,1,…,n-1],其中B中的元素B[i]=A[0]A[1]…*A[i-1]A[i+1]…*A[n-1]。不能使用除法。

2.9.2 思路1

• 直接遍历！分两段来！注意把每次循环空出一个位置来！！！
• 另外要注意不能一开始空list 然后直接赋值！只有append！或者说一开始赋予初始值 然后在这个基础之上修改即可！

2.9.3 代码1

# -*- coding:utf-8 -*-
class Solution:
    def multiply(self, A):
        # write code here
        n = len(A)
        B = list(range(n))
        # 基于分割点分别乘积得到结果
        for i in range(n):
            B[i] = 1
            # 第一段
            for j in range(i):
                B[i] *= A[j]
            # 第二段
            for k in range(i+1, n):
                B[i] *= A[k]
                   
        return B

3 参考

• https://blog.csdn.net/c406495762/article/details/79247243