【深度域适配】一、DANN与梯度反转层（GRL）详解
前言
在当前人工智能的如火如荼在各行各业得到广泛应用，尤其是人工智能也因此从各个方面影响当前人们的衣食住行等日常生活。这背后的原因都是因为如CNN、RNN、LSTM和GAN等各种深度神经网络的强大性能，在各个应用场景中解决了各种难题。
在各个领域尤其是在C端市场，深度神经网络能够迅速在近几年开花结果得益于如今当前大数据时代带来的海量数据及其标签。也就是说，当前深度学习算法是以数据集及其对应标签为驱动的，数据集及其标签的数量与质量决定了深度学习算法的性能。
如IamgeNet、VOC、COCO和CelebA等大量公开用于学术研究的数据集很好支撑起了深度学习算法在C端市场各大应用场景的算法迅速落地，极大提高了企业生产效率。但是由于数据的保密性，使得大量数据集缺少对应标签，这也使得很多在C端性能良好的深度学习算法无法快速迁移到B端场景。那么为了保证B端项目的顺利完成，企业首先需要根据项目的原始数据集结合项目需求进行大量的数据标注。同时业内目前大部分数据集标注工作都是第三方外包公司通过外包完成，则对于需要较强专业背景与业务背景的数据集不可能完全保证标签的质量，即使普通数据集保证了质量也得耗费大量的人力物力时间成本，并需要进行大量的沟通协调与监督。之后企业在人工标注的标签及其数据的基础上对公开的深度学习算法进行相关的迁移训练以满足B端项目的需求。
域适配属于迁移学习的一种，也是目前解决标签严重缺失情况下不同数据集之间模型迁移的主要思路。
一、域适配相关概念
为了下文的表述方便，我们有必要解释下域适配与迁移学习的相关概念。
通俗来说，迁移学习就是利用已有的先验知识让算法来学习新的知识，也就是说要找到先验知识与新知识之间的相似性。域适配当前迁移学习领域中解决问题的主要思路。在迁移学习和域适配中，已有的先验知识的数据集称为源域(source domain)，需要算法学习的新知识的数据集叫目标域(target domain)。通常情况下，源域和目标与之间存在较大差异即数据分布不完全相同但是肯定有有所关联。
那么在目标域与源域的数据分布不同但任务相同下的迁移学习就是域适配（领域自适应、域适应、Domain Adaptation）。也就是说域适配的主要任务就是减小源域和目标域的数据分布差异，进而实现知识的迁移。
二、DANN与梯度反转层（GRL）
域适配最先是在图像分类任务最先取得突破，主要使用CNN与域适配策略相结合，构成了DANN实现源域与目标域的图像分类任务，这也奠定了梯度反转层（GRL）在域适配的重要地位。DANN的论文下载地址为：Unsupervised Domain Adaptation by Backpropagation
在这篇论文主要提出了DANN网络，该网络的网络架构图如下图所示。在下图中，绿色部分代表特征提取网络，蓝色为图像分类网络，红色代表域分类网络。
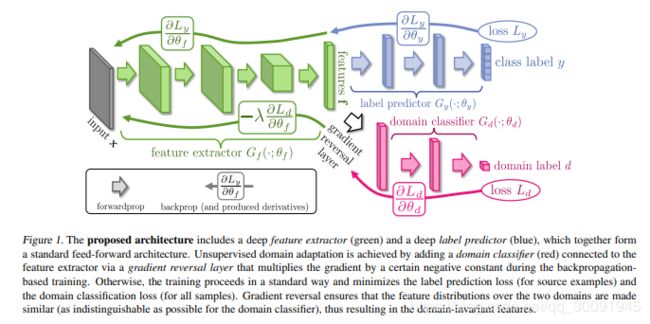在DANN的图像输入 x ∈ X x\in X x∈X ,其中 X X X代表图像输入空间，图像分类标签 y ∈ Y y\in Y y∈Y，其中 Y ( Y = { 1 , 2 , 3 , ⋯ , k } ) Y(Y\text{=}\left\{ 1,2,3,\cdots ,k \right\}) Y(Y={1,2,3,⋯,k})代表图像分类标签空间。在DANN中假定有两种数据分布：源域数据分布 S ( x , y ) \mathcal{S}(x,y) S(x,y) 和目标域数据分布 T ( x , y ) \mathcal{T}(x,y) T(x,y)。那么DANN的目标就是准确预测目标域输入图像的分类标签。
假定训练样本为 { x 1 , x 2 , ⋯ , x N } \{{{x}_{1}},{{x}_{2}},\cdots ,{{x}_{N}}\} {x1,x2,⋯,xN}分别来自源域和目标域的边缘分布 S ( x ) \mathcal{S}(x) S(x) 和 T ( x ) \mathcal{T}(x) T(x)。同时我们定义 d i d_i di为第 i i i个训练样本的域标签，其中 d i ∈ { 0 , 1 } {{d}_{i}}\in \{0,1\} di∈{0,1} 。若 d i = 0 {{d}_{i}}=0 di=0 则 x i ∼ S ( x ) {{x}_{i}}\sim \mathcal{S}(x) xi∼S(x)，反之 d i = 1 {{d}_{i}}=1 di=1 则 x i ∼ T ( x ) {{x}_{i}}\sim \mathcal{T}(x) xi∼T(x)。
在DANN训练，网络的输入为带图像分类标签的源域数据集与不带图像分类标签的目标域数据集，以及源域与目标域数据集的域分类标签。即我们知道源域数据集的图像分类标签，无目标域数据集的图像分类标签。
DANN的图像输入 x x x在训练阶段首先会经过特征提取网络 f = G f ( x ; θ f ) f={{G}_{f}}(x;{{\theta }_{f}}) f=Gf(x;θf)的映射转换为一个 D D D维的特征向量，即 f ∈ R D f\in {{\mathbb{R}}^{D}} f∈RD。然后DANN会分成两个分支即图像分类预测网络 G y ( x ; θ y ) {{G}_{y}}(x;{{\theta }_{y}}) Gy(x;θy)和域分类网络 G d ( x ; θ d ) {{G}_{d}}(x;{{\theta }_{d}}) Gd(x;θd)。源域数据输入对应的特征向量则会经过 G y ( x ; θ y ) {{G}_{y}}(x;{{\theta }_{y}}) Gy(x;θy)的映射获得对应图像分类标签预测结果。同时不管是源域输入还是目标域输入的特征向量都会经过 G d ( x ; θ d ) {{G}_{d}}(x;{{\theta }_{d}}) Gd(x;θd)得到每个输入的域分类结果。
虽然在进行图像分类的过程中，DANN只能对源域数据集数据进行图像分类，那么要想实现目标域的数据集的分类任务就必须让DANN把目标域数据看做成源域数据。那么在训练阶段我们要做的是如下两个任务，第一个则是实现源域数据集准确分类，实现现图像分类误差的最小化；第二个任务则是要混淆源域数据集和目标域数据集，实现域分类误差的最大化，混淆目标域数据集与源域数据集。那么DANN的损失函数即可以定义成如下式(1)所示：
E ( θ f , θ y , θ d ) = ∑ i = 1 , … , N d i = 0 L y ( G y ( G f ( x i ; θ f ) ; θ y ) , y i ) − λ ∑ i = 1 , … , N L d ( G d ( G f ( x i ; θ f ) ; θ d ) , y i ) = ∑ i = 1 , … , N d i = 0 L y i ( θ f , θ y ) − λ ∑ i = 1 , … , N L d i ( θ f , θ d ) (1) \begin{aligned} E\left(\theta_{f}, \theta_{y}, \theta_{d}\right) &=\sum_{i=1, \ldots, N \atop d_{i}=0} L_{y}\left(G_{y}\left(G_{f}\left(x_{i} ; \theta_{f}\right) ; \theta_{y}\right), y_{i}\right)\\ &-\lambda \sum_{i=1, \ldots, N} L_{d}\left(G_{d}\left(G_{f}\left(x_{i} ; \theta_{f}\right) ; \theta_{d}\right), y_{i}\right) \\ &=\sum_{i=1, \ldots, N \atop d_{i}=0} L_{y}^{i}\left(\theta_{f}, \theta_{y}\right)-\lambda \sum_{i=1, \ldots, N } L_{d}^{i}\left(\theta_{f}, \theta_{d}\right)\tag1 \end{aligned} E(θf,θy,θd)=di=0i=1,…,N∑Ly(Gy(Gf(xi;θf);θy),yi)−λi=1,…,N∑Ld(Gd(Gf(xi;θf);θd),yi)=di=0i=1,…,N∑Lyi(θf,θy)−λi=1,…,N∑Ldi(θf,θd)(1)
那么DANN的相关参数的最优值可以表示如下式(2)所示：
( θ ^ f , θ ^ y ) = arg min θ f , θ y E ( θ f , θ y , θ ^ d ) θ ^ d = arg max θ d E ( θ ^ f , θ ^ y , θ d ) (2) \begin{aligned} & ({{{\hat{\theta }}}_{f}},{{{\hat{\theta }}}_{y}})=\arg \underset{{{\theta }_{f}},{{\theta }_{y}}}{\mathop{\min }}\,E({{\theta }_{f}},{{\theta }_{y}},{{{\hat{\theta }}}_{d}}) \\ & {{{\hat{\theta }}}_{d}}=\arg \underset{{{\theta }_{d}}}{\mathop{\max }}\,E({{{\hat{\theta }}}_{f}},{{{\hat{\theta }}}_{y}},{{\theta }_{d}}) \\ \tag2 \end{aligned} (θ^f,θ^y)=argθf,θyminE(θf,θy,θ^d)θ^d=argθdmaxE(θ^f,θ^y,θd)(2)
从上式我们也可以看出DANN的参数求解过程与GAN的参数求解过程及其相似。DANN中域分类器的作用GAN的判别器作用十分相似。也可以说，DANN的设计思路采用了对抗学习的思想，图像分类器与域分类器在训练过程中相互对抗实现最终实现了图像分类损失与域分类损失之间的相互平衡。
那么所若使用SGD算法进行优化DANN的模型参数，DANN模型参数的梯度更新公式如下式(3)所示：
θ f = θ f − μ ( ∂ L y i ∂ θ f − λ ∂ L d i ∂ θ f ) θ y = θ y − μ ∂ L y i ∂ θ y θ d = θ d − μ ∂ L d i ∂ θ d (3) \begin{aligned} & {{\theta }_{f}}={{\theta }_{f}}-\mu (\frac{\partial L_{y}^{i}}{\partial {{\theta }_{f}}}-\lambda \frac{\partial L_{d}^{i}}{\partial {{\theta }_{f}}}) \\ & {{\theta }_{y}}={{\theta }_{y}}-\mu \frac{\partial L_{y}^{i}}{\partial {{\theta }_{y}}} \\ & {{\theta }_{d}}={{\theta }_{d}}-\mu \frac{\partial L_{d}^{i}}{\partial {{\theta }_{d}}} \\ \end{aligned} \tag3 θf=θf−μ(∂θf∂Lyi−λ∂θf∂Ldi)θy=θy−μ∂θy∂Lyiθd=θd−μ∂θd∂Ldi(3)
从式(2)与式(3)可以看出，域分类器与图像分类器的输入都来自与特征提取器，但是域分类器的目标是最大化域分类损失，混淆目标域数据与源域数据，但是图像分类器的目标是最小化图像分类损失，实现图像的精准分类。那么这就导致特征提取器在进行参数更新时，域分类损失的梯度与图像分类损失梯度方向相反。
为了避免像GAN那样分别固定生成器与鉴别器参数的方式进行分阶段训练，这也使得代码编写出现较大困难，为了编程方便，并实现真正意义上的端到端训练，DANN结构中提出了全新的梯度反转层（Gradient Reversal Layer, GRL）, 使得在反向传播过程中梯度方向自动取反，在前向传播过程中实现恒等变换，相关数学表示如下式(4)所示：
R λ ( x ) = x d R λ d x = − λ I (4) \begin{aligned} & {{R}_{\lambda }}(x)=x \\ & \frac{d{{R}_{\lambda }}}{dx}=-\lambda I \\ \end{aligned} \tag4 Rλ(x)=xdxdRλ=−λI(4)
梯度反转层主要同在特征提取器与域分类器之间，那么在反向传播过程中，域分类器的域分类损失的梯度反向传播到特征提取器的参数之前会自动取反，进而实现了类似与GAN的对抗损失。那么式(1)所表示的损失函数也可以写如下式(5)所示：
E ( θ f , θ y , θ d ) = ∑ i = 1 , … , N d i = 0 L y ( G y ( G f ( x i ; θ f ) ; θ y ) , y i ) + ∑ i = 1 , … , N L d ( G d ( R λ ( G f ( x i ; θ f ) ) ; θ d ) , y i ) (5) \begin{aligned} E\left(\theta_{f}, \theta_{y}, \theta_{d}\right) &=\sum_{i=1, \ldots, N \atop d_{i}=0} L_{y}\left(G_{y}\left(G_{f}\left(x_{i} ; \theta_{f}\right) ; \theta_{y}\right), y_{i}\right)\\ &+\sum_{i=1, \ldots, N} L_{d}\left(G_{d}\left(R_{\lambda}\left(G_{f}\left(x_{i} ; \theta_{f}\right)\right) ; \theta_{d}\right), y_{i}\right) \\ \tag5 \end{aligned} E(θf,θy,θd)=di=0i=1,…,N∑Ly(Gy(Gf(xi;θf);θy),yi)+i=1,…,N∑Ld(Gd(Rλ(Gf(xi;θf));θd),yi)(5)
当然在梯度反转层（GRL）中，参数 λ \lambda λ并不是固定值，而是动态变化的。其变化表达式如式(6)所示：
λ p = 2 1 + exp ( − γ ⋅ p ) − 1 (6) {{\lambda }_{p}}=\frac{2}{1+\exp (-\gamma \cdot p)}-1\tag6 λp=1+exp(−γ⋅p)2−1(6)
在式(6)中， p p p代表迭代进程相对值，即当前迭代次数与总迭代次数的比率， γ \gamma γ为常数10。同时，在DANN架构中学习率也是随着迭代进程变换的，变换公式如式(7)所示：
μ p = μ 0 ( 1 + α ⋅ p ) β (7) {{\mu }_{p}}=\frac{{{\mu }_{0}}}{{{(1+\alpha \cdot p)}^{\beta }}}\tag7 μp=(1+α⋅p)βμ0(7)
其中 μ 0 {\mu }_{0} μ0为初始学习率，其值为0.01， p p p代表迭代进程相对值，即当前迭代次数与总迭代次数的比率， α \alpha α和 β \beta β属于超参数， α = 10 , β = 0.75 \alpha=10,\beta=0.75 α=10,β=0.75。
三、实验结论
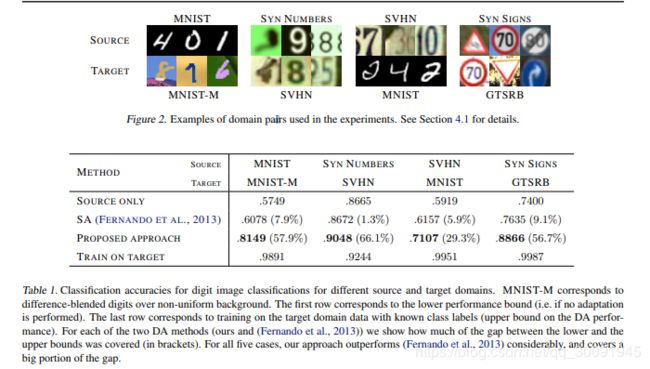
在论文中，作者在小数集和大数据集上做了相关实验。小数据集下主要使用了MNIST、MNIST-M、SYN NUMBERS、SVHN、 SYN SIGNS和 GTSRB数据集，主要分别使用一种数据集作为源域，另一种作为目标域来训练不同CNN架构的DANN，实验结果如下：
大数据集的域适应训练实验结果如下：
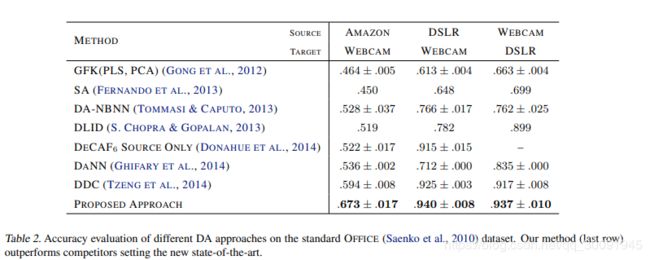
上述实验中，不同数据集对应的DANN网络架构如下所示：
总结
结论：
- 在Unsupervised Domain Adaptation by
Backpropagation论文中主要提出了DANN（域适应深度网络）架构，主要由特征提取网络、图像分类网络与域分类网络构成，图像分类网络与域分类网络共享特征提取网络的参数。 - DANN的目标分成两个：最小化图像分类损失用于准确分类图像；最大化域分类损失用于混淆目标域数据与源域数据。
- 提出了梯度反转层（GRL），该层用于特征提取网络与域分类网络之间，反向传播过程中实现梯度取反，进而构造出了类似于GAN的对抗损失，又通过该层避免了GAN的两阶段训练过程。
- 论文实验证明，无论是小数据集还是大数据集中，DANN和GRL在图像分类任务中取得了较高的分类精度，成功解决了数据集缺少标签的难题，即实现了无监督的图像分类。
- GAN可以看成是域适配的一种，GAN从某种意义上讲实现了域与域之间的像素级别自适应，而GRL则实现了域与域之间的特征级别自适应。
**
在下一篇博客：【深度域适配】二、利用DANN实现MNIST和MNIST-M数据集迁移训练中我们将主要聚焦于DANN与GRL的tensorflow实现，并利用DANN实现MNiST和MNIST-M数据集之间的域适配训练。