多机器人协同编队算法原理及实现
ROS及SLAM进阶教程(八)机器人协同编队算法原理及实现
- 图论基础
- 基于一致性的编队控制算法
- 编队控制算法原理
- 编队算法仿真实现
多机器人协同编队需要将理论和实践紧密地结合起来,其应用包括编队队形生成、保持、变换和路径规划与避障等等都是基于图论的理论基础完成的。
图论基础
控制协同多智能体动态系统是通过通信图进行相互联系的动力学问题,通信图表明了各个节点之间的信息流。协同控制的目标是为各个节点设计控制协议,以保证所有节点在某种特定意义上的状态同步行为。在协同系统中,任何控制协议都必须按照其所规定的图拓扑结构进行分布式控制,也就是说,每个节点的控制协议只允许依赖于关于该节点及其在图中的邻居节点的信息,拓扑图施加的通信限制可能会严重限制每个节点上的本地分布式控制协议所能完成的工作。
在多机器人协同编队中,我们关注的是动态系统的行为和相互作用,这些动态系统通过通信网络的链接相互联系,该通信网络被建模为具有与系统间允许的信息流相对应的有向边的图,编队中的每个机器人被建模为图中的节点,那么最基本的问题就变为了图拓扑如何与节点的本地反馈控制协议交互,以生成互连节点的整体行为,下面展示一些在研究多机器人协同编队中必不可少的基本的图论概念。
一个拓扑图可以表示为 G = ( V , E ) G=(V, E) G=(V,E),其中 V = { v 1 , … , v N } V=\{ v_1,…,v_N \} V={v1,…,vN}表示N个节点的集合,E表示E条边的集合,假设图为简单有向图,即 ( v i , v j ) ∉ E (v_i,v_j) \notin E (vi,vj)∈/E并且同一对节点之间没有多条边,集合E中的元素 ( v i , v j ) (v_i,v_j) (vi,vj)表示从节点vj指向节点 v i v_i vi的边,在编队中表示信息从节点 v j v_j vj机器人流向节点 v i v_i vi机器人,节点 v i v_i vi机器人的出度 d i o d_i^o dio表示以其为数据发送端的边的数量,入度 d i d_i di表示以其为数据接收端的边的数量。
图的结构和性质可以通过研究与图相关的某些矩阵的性质来研究,这就是代数图论。给定边的权值 a i j a_{ij} aij后,该图便可以被一个邻接矩阵或连通矩阵 A = [ a i j ] A=[a_{ij}] A=[aij]表示,其中当 ( v i , v j ) ∉ E (v_i,v_j) \notin E (vi,vj)∈/E时 a i j = 1 a_{ij}=1 aij=1,否则 a i j = 0 a_{ij}=0 aij=0,则此时节点i的加权入度可表示为矩阵A第i行所有值之和,如式(1)所示:
d i = ∑ j = 1 N a i j d_i=\sum_{j=1}^N a_{ij} di=j=1∑Naij
则其加权出度可表示为式(2):
d i o = ∑ j = 1 N a j i d_i^o=\sum_{j=1}^N a_{ji} dio=j=1∑Naji
入度和出度都为图的局部性质,在编队拓扑通信中,其出度可以反映出节点对编队其他机器人的影响程度,即当出度越大,该节点机器人对编队一致性的影响越大。
定义一个对角入度矩阵 D = d i a g d i D=diag{d_i} D=diagdi和图拉普拉斯矩阵L=D-A,图的许多性质都可以以图拉普拉斯矩阵的性质被研究,其在动态多节点系统图论研究中有极其重要的意义,一个有向图及其伴随矩阵、对角矩阵和拉普拉斯矩阵如下所示:
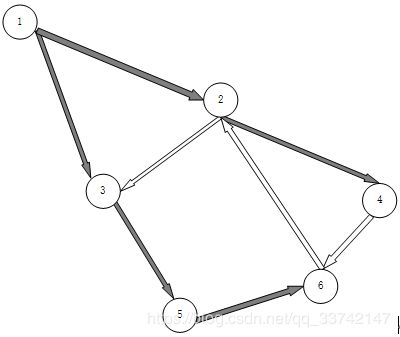
其对应的矩阵如下所示:
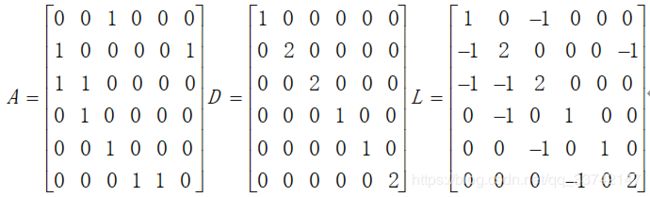
图拉普拉斯矩阵L的特征结构在图上动力系统分析中起着关键作用,下面对L的特征值情况进行分析,定义图拉普拉斯矩阵的约当形式如下:
L = M J M − 1 L=MJM^{-1} L=MJM−1
其中约当形式矩阵J和变换矩阵M为:

其中特征值 λ i \lambda_i λi和M的右特征向量 v i v_i vi满足
( λ i I − L ) v i = 0 (\lambda_i I -L)v_i=0 (λiI−L)vi=0
其中I为单位矩阵。M左特征向量wi满足
w i ( λ i I − L ) = 0 w_i(\lambda_i I -L)=0 wi(λiI−L)=0
w i T v i = 1 w_i^Tv_i=1 wiTvi=1
由于矩阵L所有行元素之和为0,故当且仅当L有唯一的特征向量c使得Lc=0,其特征值为0,即L的秩为N-1时图G有一个生成树,这对于形成编队的稳定性有重要的作用。
基于一致性的编队控制算法
本文采用领航者-跟随者编队中的分布式控制结构,在前文图论的基础上采用下文给出的一致性算法实现了编队控制。
编队控制算法原理
领航者-跟随者编队是一种经典的编队形式,其基于一致性的一阶编队算法主要思想在于控制好领航者和跟随者之间的相对位置和速度等状态量,这些量达到一定的稳定状态时就实现了编队队形,其中领航机器人扮演着至关重要的角色。
编队系统的一阶连续系统模型如下:
x ˙ i = u i \dot{x}_i=u_i x˙i=ui
x i x_i xi, u i u_i ui分别表示节点i的状态量和输入量,且 x i , u i ∈ R n x_i,u_i \in R^n xi,ui∈Rn,n表示状态量的维度,在理想情况下,考虑如下形式的控制输入
u i = ∑ j ∈ N i a i j ( x j − x i ) u_i=\sum_{j \in N_i}a_{ij}(x_j-x_i) ui=j∈Ni∑aij(xj−xi)
其中 a i j a_{ij} aij为编队邻接矩阵元素, N i N_i Ni为成员i的邻居集合,将(2-8)代入(2-7)再引入全局状态向量 x = [ x 1 , . . . , x n ] T ∈ R n x=[x_1,...,x_n]^T\in R^n x=[x1,...,xn]T∈Rn可得到全局动态关系为:
x ˙ = − D x + A x = − L x \dot{x}=-Dx+Ax=-Lx x˙=−Dx+Ax=−Lx
从上式我们可以看出编队的闭环动态特性取决于L矩阵。此外,当且仅当编队的拓扑图G具有一棵生成树时,-L特征值均位于复平面左半平面,因此(2-8)能保证系统达到一致性,最终状态值为:
c = ∑ i = 1 N p i x i ( 0 ) c=\sum_{i=1}^Np_ix_i(0) c=i=1∑Npixi(0)
在离散时间下,(2-7)可化为:
x i ( k + 1 ) = x i ( k ) + u i ( k ) x_i(k+1)=x_i(k)+u_i(k) xi(k+1)=xi(k)+ui(k)
在本课题中,假设一个场景为领航者带领其他机器人完成一段距离的运动,从起点出发向一个目标点运动,理想情况下编队中跟随者的的算法采用如下形式
u i ( k ) = ε ∑ j ∈ N i a i j ( x j ( k ) − x i ( k ) − r i j ( k ) ) u_i(k)=\varepsilon\sum_{j\in N_i}a_{ij}(x_j(k)-x_i(k)-r_{ij}(k)) ui(k)=εj∈Ni∑aij(xj(k)−xi(k)−rij(k))
其中 ε > 0 \varepsilon >0 ε>0, r i j r_{ij} rij表示机器人i和机器人j之间的相对位置,与他们之间的距离相关,而领航者N的控制算法为
u N ( k ) = m + k D ( k ) + ∑ i ∈ N i a N i r N i ( k ) u_N(k)=m+kD(k)+\sum_{i\in N_i}a_{Ni}r_{Ni}(k) uN(k)=m+kD(k)+i∈Ni∑aNirNi(k)
其中r_{nj}表示领航者与其他机器人之间的相对位置,m和k均为常数,D(k)表示k时刻领航者到目标点的距离,领航者的速度受到相邻节点的影响以及领航者到目标点的距离影响。
以上是最基本的算法,除此之外还有对如平均一致性、运动不变量等的研究,因篇幅有限,这些算法不再赘述。
编队算法仿真实现
本文验证编队一致性算法,使用五个机器人按照领航者-跟随者的形式组成实验的机器人编队,找定一个稳定的通信拓扑矩阵A,如
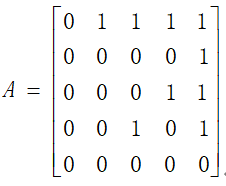
使用此通信拓扑矩阵后编队队形及其通信拓扑结构如下图所示:
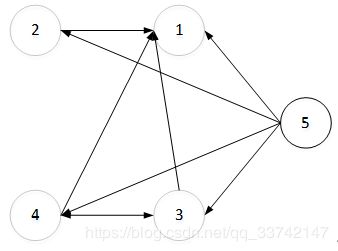
其中箭头表示信息流方向,从上图可以看出节点五的出度最大,故节点五为关键节点,即为领航机器人,而节点一出度为0,其对编队的影响最小。
博主git上给出了MATLAB的仿真和ROS中基于python的仿真,有需要请到git自取,有用的话一定要点赞收藏关注支持博主哈
以上是关于多机器协同编队的算法原理讲解与代码实现。后续还会介绍基于编队的避障算法。
码字不易,喜欢的话请点赞收藏关注哦,您的支持是博主最大的动力。
博主有两年多ROS的使用经验,目前仍在不停研究中。本系列ROS及SLAM进阶教程将涵盖ROS的进阶功能使用、机器人SLAM及导航的设计及研究等领域,持续不断更新中。如果大家有相关问题或发现作者漏洞欢迎私戳,同时欢迎关注收藏。
同时欢迎关注博主Git:
https://github.com/redglassli