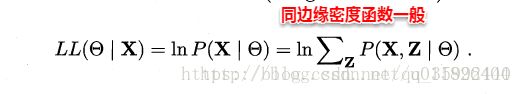贝叶斯网络与EM算法
贝叶斯网与EM算法
一、贝叶斯网
贝叶斯网络亦称为“信念网”,他借助有向无环图来刻画属性之间的依赖关系,并使用条件概率表来描述属性的联合概率分布。
具体来说,一个贝叶斯网B由结构G和参数 θ θ 两部分构成,即 B=(G,θ) B = ( G , θ ) 网络结构G是一个有向无环图,其每一个节点对应于一个属性,若两个属性有直接依赖关系,则它们由一条边连接起来;参数 θ θ 定量描述这种依赖关系,假设属性 xi x i 在G中的父结点集为 πi π i ,则 θ θ 包含了每个属性的条件概率表 θxi|πi=PB(xi|πi) θ x i | π i = P B ( x i | π i )
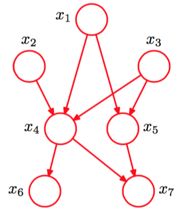
下面是一个例子:
注,图中每个属性对应的表格就是每个属性的条件概率表 θ θ
1.1 结构
贝叶斯网有效地表达了属性间的条件独立性,给定父节点集,贝叶斯网假设每个属性与它的非后裔属性独立,于是
B=(G,θ) B = ( G , θ ) 将属性 x1,x2,x3,⋯,xd x 1 , x 2 , x 3 , ⋯ , x d 的联合概率分布定义为
P(x1,x2,x3,x4,x5,x6,x7)=P(x1)P(x2)P(x3)P(x4∣x1,x2,x3)P(x5∣x1,x3)P(x6∣x4)P(x7∣x4,x5)P(x1,x2,x3,x4,x5,x6,x7)=P(x1)P(x2)P(x3)P(x4∣x1,x2,x3)P(x5∣x1,x3)P(x6∣x4)P(x7∣x4,x5) P ( x 1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 ) = P ( x 1 ) P ( x 2 ) P ( x 3 ) P ( x 4 ∣ x 1 , x 2 , x 3 ) P ( x 5 ∣ x 1 , x 3 ) P ( x 6 ∣ x 4 ) P ( x 7 ∣ x 4 , x 5 ) P ( x 1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 ) = P ( x 1 ) P ( x 2 ) P ( x 3 ) P ( x 4 ∣ x 1 , x 2 , x 3 ) P ( x 5 ∣ x 1 , x 3 ) P ( x 6 ∣ x 4 ) P ( x 7 ∣ x 4 , x 5 )
下面介绍贝叶斯网络的三种基本结构:
1.2 学习
若网络结构已知,则属性间的依赖关系已知,则贝叶斯网络的学习过程相对简单,只需对训练样本计数,估计出每个结点的条件概率表即可,但在现实应用中我们往往并不知晓网络结构,于是,贝叶斯学习的首要任务就是根据训练数据集来找出结构最恰当的贝叶斯网。
评分搜索就是求解这一类问题的常用办法,具体来说,我们先定义一个评分函数,以此估计贝叶斯网与训练数据的契合程度,然后基于这个评分函数来寻找结构最优的贝叶斯网。
常用的评分函数基于信息论准则,学习的目标是找到一个能以最短编码长度描述训练数据的模型,该编码的长度包括了描述模型自身所需的字节长度和使用该模型描述数据所需的字节长度。对于贝叶斯网学习而言,模型就是一个贝叶斯网,同时,每个贝叶斯网描述了一个在训练数据上的概率分布,自有一套编码机制能使那些经常出现的样本有更短的编码。于是,我们应该选择那个综合编码长度最短的贝叶斯网,这就是“最小描述长度准则”。
该方法的数学描述:
给定训练集 D={x1,x2,⋯,xm} D = { x 1 , x 2 , ⋯ , x m } ,贝叶斯网 B=(G,θ) B = ( G , θ ) 在D上的评分函数可写成
其中,|B|是贝叶斯网的参数个数; f(θ) f ( θ ) 表示描述每个参数 θ θ 所需的字节数,而:
它是贝叶斯网B的对数似然,他计算B所对应的概率分布 PB P B 对D的描述得有多好,于是,学习任务就转化为一个优化任务,寻找一个贝叶斯网B使得评分函数s(B|D)最小。
二、EM算法
EM(Expectation-Maximization)算法是一种常用的估计参数隐变量的利器,也称为“期望最大算法”,是数据挖掘的十大经典算法之一。EM算法主要应用于训练集样本不完整即存在隐变量时的情形(例如某个属性值未知),通过其独特的“两步走”策略能较好地估计出隐变量的值。
2.1 EM算法思想
EM是一种迭代式的方法,它的基本思想就是:若样本服从的分布参数θ已知,则可以根据已观测到的训练样本推断出隐变量Z的期望值(E步),若Z的值已知则运用最大似然法估计出新的θ值(M步)。重复这个过程直到Z和θ值不再发生变化。
简单来讲:假设我们想估计A和B这两个参数,在开始状态下二者都是未知的,但如果知道了A的信息就可以得到B的信息,反过来知道了B也就得到了A。可以考虑首先赋予A某种初值,以此得到B的估计值,然后从B的当前值出发,重新估计A的取值,这个过程一直持续到收敛为止。

现在再来回想聚类的代表算法K-Means:【首先随机选择类中心=>将样本点划分到类簇中=>重新计算类中心=>不断迭代直至收敛】,不难发现这个过程和EM迭代的方法极其相似,事实上,若将样本的类别看做为“隐变量”(latent variable)Z,类中心看作样本的分布参数θ,K-Means就是通过EM算法来进行迭代的,与我们这里不同的是,K-Means的目标是最小化样本点到其对应类中心的距离和,上述为极大化似然函数。
2.2 EM算法数学推导
当样本属性值都已知时,我们很容易通过极大化对数似然,接着对每个参数求偏导计算出参数的值。但当存在隐变量时,就无法直接求解,此时我们通常最大化已观察数据的对数“边际似然”(marginal likelihood),其中X表示已知的属性值,Z表示隐变量, θ θ 表示参数。
这时候,通过边缘似然将隐变量Z引入进来,对于参数估计,现在与最大似然不同的只是似然函数式中多了一个未知的变量Z,也就是说我们的目标是找到适合的参数θ和Z让L(θ)最大,这样我们也可以分别对未知的参数θ和Z求偏导,再令其等于0。
然而观察上式可以发现,和的对数(ln(x1+x2+x3))求导十分复杂,那能否通过变换上式得到一种求导简单的新表达式呢?这时候 Jensen不等式就派上用场了,先回顾一下高等数学凸函数的内容:
Jensen’s inequality:过一个凸函数上任意两点所作割线一定在这两点间的函数图象的上方。理解起来也十分简单,对于凸函数f(x)”>0,即曲线的变化率是越来越大单调递增的,所以函数越到后面增长越厉害,这样在一个区间下,函数的均值就会大一些了。
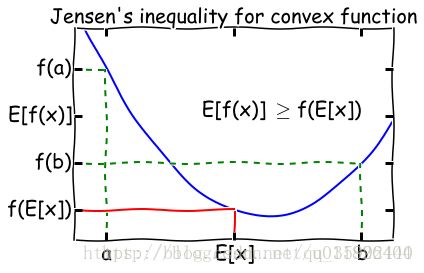
因为ln(*)函数为凹函数,故可以将上式“和的对数”变为“对数的和”,这样就很容易求导了。

接着求解Qi和θ:首先固定θ(初始值),通过求解Qi使得J(θ,Q)在θ处与L(θ)相等,即求出L(θ)的下界;然后再固定Qi,调整θ,最大化下界J(θ,Q)。不断重复两个步骤直到稳定。通过jensen不等式的性质,Qi的计算公式实际上就是后验概率:
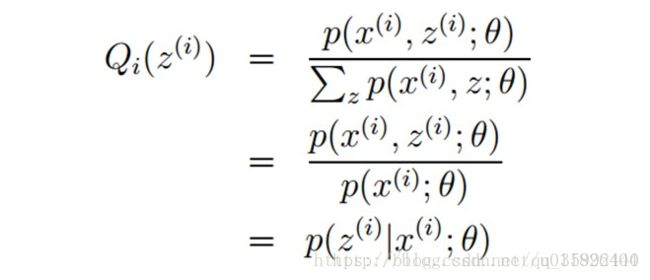
 通过数学公式的推导,简单来理解这一过程:固定θ计算Q的过程就是在建立L(θ)的下界,即通过jenson不等式得到的下界(E步);固定Q计算θ则是使得下界极大化(M步),从而不断推高边缘似然L(θ)。从而循序渐进地计算出L(θ)取得极大值时隐变量Z的估计值。
通过数学公式的推导,简单来理解这一过程:固定θ计算Q的过程就是在建立L(θ)的下界,即通过jenson不等式得到的下界(E步);固定Q计算θ则是使得下界极大化(M步),从而不断推高边缘似然L(θ)。从而循序渐进地计算出L(θ)取得极大值时隐变量Z的估计值。
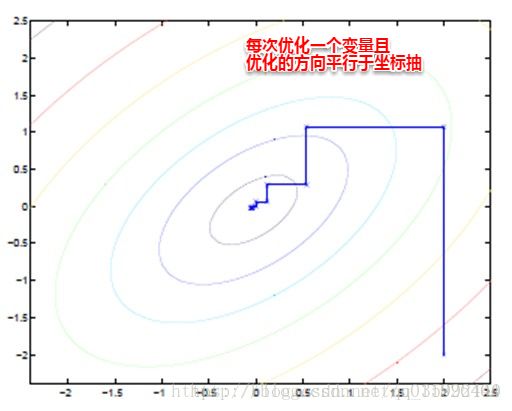
EM算法也可以看作一种“坐标下降法”,首先固定一个值,对另外一个值求极值,不断重复直到收敛。这时候也许大家就有疑问,问什么不直接这两个家伙求偏导用梯度下降呢?这时候就是坐标下降的优势,有些特殊的函数,例如曲线函数 z=y2+x2+x2y+xy+… z = y 2 + x 2 + x 2 y + x y + … ,无法直接求导,这时如果先固定其中的一个变量,再对另一个变量求极值,则变得可行。
8.3 EM算法流程
看完数学推导,算法的流程也就十分简单了,这里有两个版本,版本一来自西瓜书,周天使的介绍十分简洁;版本二来自于大牛的博客。结合着数学推导,自认为版本二更具有逻辑性,两者唯一的区别就在于版本二多出了红框的部分
版本一:
版本二: