RNN前向反向传播（花书《深度学习》10.2循环神经网络）

最近在阅读花书《深度学习》10.2循环神经网络，对该节公式（10.21）有所疑惑，主要是发现该公式的梯度表示维度计算有问题，且与（10.22）~（10.28）有矛盾，因此本文基于刘建平老师原文原文链接：循环神经网络(RNN)模型与前向反向传播算法，添加了部分基础知识和更细节的公式推导，探究问题所在。感谢刘老师！！！刘建平老师博客地址

1 预备数学

1.1 tanh与导数

tanh函数是一种激活函数，也称双曲正切函数，取值范围为[-1,1],计算公式如下。
$$f(z)=\tanh (z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$
其中z是标量，根据复合函数求导，其导数为：

$$\begin{array}{rl}{f}^{\prime }(z)& =\frac{d\frac{e^z-e^{-z}}{e^z+e^{-z}}}{dz}=\frac{\left(e^z+e^{-z}\right)\left(e^z+e^{-z}\right)-\left(e^z-e^{-z}\right)\left(e^z-e^{-z}\right)}{{\left(e^z+e^{-z}\right)}^2}\\ & =1-(f(z){)}^2\end{array}$$
若z是d维向量，则导数为对角矩阵（diag不加转置的原因是diag是对角，加不加都一样）
$$f^{\prime }(\mathbf{z})=\frac{\partial f(\mathbf{z})}{\partial \mathbf{z}}=diag(1-(f(\mathbf{z}){)}^2)=\frac{\partial diag(1-{(f(\mathbf{z}))}^2)\mathbf{z}}{\partial \mathbf{z}}\mathbf{z}\in R^d{f}^{\prime }(\mathbf{z})\in R^{d\times d}$$

1.2 softmax

在分类任务中，通常用交叉熵（Cross Entropy）衡量预测分布与真实分布的相近程度，其公式为
$$CE(\mathbf{y},\hat{\mathbf{y}})=-\sum y_i\log {\hat{y}}_i$$
其中y是真实分布，one-hot编码，y_hat是预测分布，经由softmax产生且有

$$\begin{array}{rl}\hat{\mathbf{y}}& =\mathrm{softmax}(\mathbf{\theta })\\ \frac{\partial CE}{\partial \mathbf{\theta }}& =\hat{\mathbf{y}}-\mathbf{y}\end{array}$$

2 RNN前向传播

2.1 RNN结构

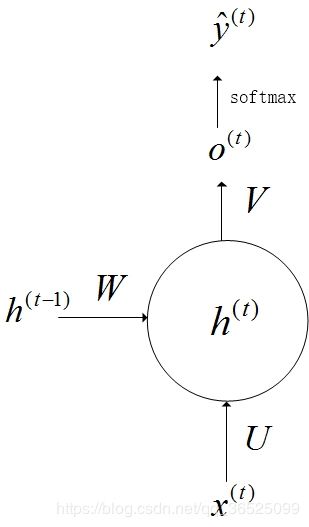
上图中左边是RNN模型没有按时间展开的图，如果按时间序列展开，则是上图中的右边部分。我们重点观察右边部分的图。
1）$x^{(t)}$代表在序列索引号t时训练样本的输入。同样的，$x^{(t-1)}$和$x^{(t+1)}$代表在序列索引号t−1和t+1时训练样本的输入.
2）$h^{(t)}$代表在序列索引号t时模型的隐藏状态。$h^{(t)}$由$x^{(t)}$和$h^{(t-1)}$共同决定。
3）$o^{(t)}$代表在序列索引号t时模型的输出。$o^{(t)}$只由模型当前的隐藏状态$h^{(t)}$决定。
4）$L^{(t)}$代表在序列索引号t时模型的损失函数。
5）$y^{(t)}$代表在序列索引号t时训练样本序列的真实输出。
6）$U$,$W$,$V$这三个矩阵是我们的模型的线性关系参数，它在整个RNN网络中是共享的，这点和DNN很不相同。 也正因为是共享了，它体现了RNN的模型的“循环反馈”的思想。

2.1 RNN数学描述

根据上图所示t时刻的隐藏状态$h^{(t)}$由t-1时刻的隐藏状态$h^{(t-1)}$和t时刻的输入$x^{(t)}$决定
$$h^{(t)}=\sigma (z^{(t)})=\sigma (U{x}^{(t)}+W{h}^{(t-1)}+b)$$
其中$\sigma$为激活函数，通常为tanh，t时刻的输出$o^{(t)}$和预测${\hat{y}}^{(t)}$为

$$\begin{array}{l}{o}^{(t)}=V{h}^{(t)}+c\\ {\hat{y}}^{(t)}=\mathrm{softmax}\left(o^{(t)}\right)\end{array}$$

3 RNN反向传播

    有了RNN前向传播算法的基础，就容易推导出RNN反向传播算法的流程了。RNN反向传播算法的思路和DNN是一样的，即通过梯度下降法一轮轮的迭代，得到合适的RNN模型参数U,W,V,b,c。由于我们是基于时间反向传播，所以RNN的反向传播有时也叫做BPTT(back-propagation through time)。当然这里的BPTT和DNN也有很大的不同点，即这里所有的U,W,V,b,c在序列的各个位置是共享的，反向传播时我们更新的是相同的参数。
    为了简化描述，这里的损失函数我们为交叉熵损失函数，输出的激活函数为softmax函数，隐藏层的激活函数为tanh函数。
    对于RNN，由于我们在序列的每个位置都有损失函数，因此最终的损失L为：
$$L=\sum _{t=1}^T{L}^{(t)}$$
其中$L^{(t)}$为t时刻的预测值与真实值的交叉熵，即
$$L^{(t)}=CE({\hat{y}}^{(t)},y^{(t)})$$
根据1.2有
$$\frac{\partial L^{(t)}}{\partial o^{(t)}}={\hat{y}}^{(t)}-y^{(t)}$$
OK,那我们就来计算各个参数的梯度了，首先对$c$和$V$求导
$$\frac{\partial L}{\partial c}=\sum _{t=1}^T\frac{\partial L^{(t)}}{\partial c}=\sum _{t=1}^T\frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial c}=\sum _{t=1}^T{\hat{y}}^{(t)}-y^{(t)}$$
$$\begin{array}{rl}\frac{\partial L}{\partial V}& =\sum _{t=1}^T\frac{\partial L^{(t)}}{\partial V}=\sum _{t=1}^T\frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial V}\\ & =\sum _{t=1}^T\left({\hat{y}}^{(t)}-y^{(t)}\right)\frac{\partial V{h}^{(t)}}{\partial V}=\sum _{t=1}^T\frac{\partial V{h}^{(t)}{\left({\hat{y}}^{(t)}-y^{(t)}\right)}^{\mathrm{T}}}{\partial V}\\ & =\sum _{t=1}^T\left({\hat{y}}^{(t)}-y^{(t)}\right){\left(h^{(t)}\right)}^{\mathrm{T}}\end{array}$$
    但是W,U,b的梯度计算就比较的复杂了。从RNN的模型可以看出，在反向传播时，在在某一序列位置t的梯度损失由当前位置的输出对应的梯度损失和序列索引位置t+1时的梯度损失两部分共同决定。对于W在某一序列位置t的梯度损失需要反向传播一步步的计算。我们定义序列索引t位置的隐藏状态的梯度为：
$${\delta }^{(t)}=\frac{\partial L}{\partial h^{(t)}}$$
这样我们可以像DNN一样从${\delta }^{(t+1)}$递推${\delta }^{(t)}$,因此${\delta }^{(t)}$计算公式如下:
$${\delta }^{(t)}=\frac{\partial L}{\partial h^{(t+1)}}\frac{\partial h^{(t+1)}}{\partial h^{(t)}}+\frac{\partial L}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}$$
前一部分为下一时刻t+1带来的梯度，后一部分为t时刻的输出带来的梯度,展开可得：
$$\begin{array}{rl}{\delta }^{(t)}& ={\delta }^{(t+1)}\frac{\partial h^{(t+1)}}{\partial z^{(t+1)}}\frac{\partial z^{(t+1)}}{\partial h^{(t)}}+\left({\hat{y}}^{(t)}-y^{(t)}\right)\frac{\partial V{h}^{(t)}}{\partial h^{(t)}}\\ & ={\delta }^{(t+1)}\frac{\partial \mathrm{diag}\left(1-{\left(h^{(t+1)}\right)}^2\right)z^{(t+1)}}{z^{(t+1)}}\frac{\partial W{h}^{(t)}}{\partial h^{(t)}}+\left({\hat{y}}^{(t)}-y^{(t)}\right)\frac{\partial V{h}^{(t)}}{\partial h^{(t)}}\\ & =\frac{\partial {\left({\delta }^{(t+1)}\right)}^{\mathrm{T}}\mathrm{diag}\left(1-{\left(h^{(t+1)}\right)}^2\right)z^{(t+1)}}{\partial h^{(t)}}+V^{\mathrm{T}}\left({\hat{y}}^{(t)}-y^{(t)}\right)\\ & =\mathrm{diag}\left(1-{\left(h^{(t+1)}\right)}^2\right){\delta }^{(t+1)}\frac{\partial W{h}^{(t)}}{\partial h^{(t)}}+V^{\mathrm{T}}\left({\hat{y}}^{(t)}-y^{(t)}\right)\\ & =W^{\mathrm{T}}\mathrm{diag}\left(1-{\left(h^{(t+1)}\right)}^2\right){\delta }^{(t+1)}+V^{\mathrm{T}}\left({\hat{y}}^{(t)}-y^{(t)}\right)\end{array}$$
与花书公式（10.21）不同，区别在于${\delta }^{(t+1)}$与diag的位置顺序，但根据维度计算后发现，花书应该有误，上述公式正确。
因为T是序列最后一个时刻，所以${\delta }^{(T)}$的梯度只来自于T时刻的输出，即
$${\delta }^{(T)}=\frac{\partial L}{\partial o^{(T)}}\frac{\partial o^{(T)}}{\partial h^{(T)}}=({\hat{y}}^{(T)}-y^{(T)})\frac{\partial V{h}^{(T)}}{\partial h^{(T)}}=V^{\mathrm{T}}({\hat{y}}^{(T)}-y^{(T)})$$
则对于W,b,U的梯度为：
$$\begin{array}{rl}\frac{\partial L}{\partial W}& =\sum _{t=1}^T\frac{\partial L}{\partial h^{(t)}}\frac{\partial h^{(t)}}{\partial W}=\sum _{t=1}^T{\delta }^{(t)}\frac{\partial h^{(t)}}{\partial z^{(t)}}\frac{\partial z^{(t)}}{\partial W}\\ & =\sum _{t=1}^T\mathrm{diag}\left(1-{\left(h^{(t)}\right)}^2\right){\delta }^{(t)}\frac{\partial W{h}^{(t-1)}}{\partial W}\\ & =\sum _{t=1}^T\mathrm{diag}\left(1-{\left(h^{(t)}\right)}^2\right){\delta }^{(t)}{\left(h^{(t-1)}\right)}^{\mathrm{T}}\end{array}$$
$$\begin{array}{rl}\frac{\partial L}{\partial b}& =\sum _{t=1}^T\frac{\partial L}{\partial h^{(t)}}\frac{\partial h^{(t)}}{\partial b}=\sum _{t=1}^T{\delta }^{(t)}\frac{\partial h^{(t)}}{\partial z^{(t)}}\frac{\partial z^{(t)}}{\partial b}\\ & =\sum _{t=1}^T\mathrm{diag}\left(1-{\left(h^{(t)}\right)}^2\right){\delta }^{(t)}\frac{\partial b}{\partial b}\\ & =\sum _{t=1}^T\mathrm{diag}\left(1-{\left(h^{(t)}\right)}^2\right){\delta }^{(t)}\end{array}$$
$$\begin{array}{rl}\frac{\partial L}{\partial U}& =\sum _{t=1}^T\frac{\partial L}{\partial h^{(t)}}\frac{\partial h^{(t)}}{\partial U}=\sum _{t=1}^T{\delta }^{(t)}\frac{\partial h^{(t)}}{\partial z^{(t)}}\frac{\partial U{x}^{(t)}}{\partial U}\\ & =\sum _{t=1}^T\mathrm{diag}\left(1-{\left(h^{(t)}\right)}^2\right){\delta }^{(t)}\frac{\partial U{x}^{(t)}}{\partial U}\\ & =\sum _{t=1}^T\mathrm{diag}\left(1-{\left(h^{(t)}\right)}^2\right){\delta }^{(t)}{\left(x^{(t)}\right)}^{\mathrm{T}}\end{array}$$