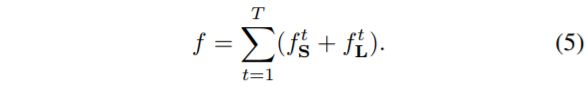Paper：《Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields ∗》翻译并解读

Paper：《Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields ∗》翻译并解读

 

 

目录

Abstract

1、Introduction   

2. Method

2.1. Simultaneous Detection and Association  

2.2. Confidence Maps for Part Detection

2.3. Part Affinity Fields for Part Association  

2.4. Multi-Person Parsing using PAFs

3. Results

3.1. Results on the MPII Multi-Person Dataset

3.2. Results on the COCO Keypoints Challenge

3.3. Runtime Analysis

4. Discussion

Acknowledgements

References

---

 

 

论文：《Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields ∗》

Abstract

We present an approach to efficiently detect the 2D pose  of multiple people in an image. The approach uses a nonparametric  representation, which we refer to as Part Affinity  Fields (PAFs), to learn to associate body parts with individuals  in the image. The architecture encodes global context,  allowing a greedy bottom-up parsing step that maintains  high accuracy while achieving realtime performance,  irrespective of the number of people in the image. The architecture  is designed to jointly learn part locations and  their association via two branches of the same sequential  prediction process. Our method placed first in the inaugural  COCO 2016 keypoints challenge, and significantly exceeds  the previous state-of-the-art result on the MPII MultiPerson  benchmark, both in performance and efficiency.

我们提出了一种有效检测图像中多人二维姿态的方法。该方法使用非参数表示（我们称之为部分关联区域（PAFs））来学习将身体部位与图像中的个体关联起来。该体系结构对全局上下文进行编码，允许贪婪的自下而上的解析步骤，在实现实时性能的同时保持高精度，而不考虑图像中的人数。该体系结构旨在通过同一序列预测过程的两个分支联合学习零件位置及其关联。我们的方法在首届COCO 2016关键点挑战赛中排名第一，在性能和效率方面都大大超过了之前MPII多人测试的最新结果。

 

1、Introduction   

Human 2D pose estimation—the problem of localizing anatomical keypoints or “parts”—has largely focused on finding body parts of individuals [8, 4, 3, 21, 33, 13, 25, 31, 6, 24]. Inferring the pose of multiple people in images, especially socially engaged individuals, presents a unique set of challenges. First, each image may contain an unknown number of people that can occur at any position or scale. Second, interactions between people induce complex spatial interference, due to contact, occlusion, and limb articulations, making association of parts difficult. Third, runtime complexity tends to grow with the number of people in the image, making realtime performance a challenge.	人体二维姿势估计解剖学关键点或“部位”的定位问题主要集中在寻找个体的身体部位[8，4，3，21，33，13，25，31，6，24]。在图像中推断出多人的姿势，特别是团体中的个体，是一组独特的挑战。首先，每个图像可能包含未知数量的人，这些人可以出现在任何位置或规模。其次，由于接触、咬合和肢体关节，人与人之间的相互作用会导致复杂的空间干扰，使得部件之间的关联变得困难。第三，运行时间复杂度随着人数的增加而增加。
Figure 1. Top: Multi-person pose estimation. Body parts belonging  to the same person are linked. Bottom left: Part Affinity Fields  (PAFs) corresponding to the limb connecting right elbow and right  wrist. The color encodes orientation. Bottom right: A zoomed in  view of the predicted PAFs. At each pixel in the field, a 2D vector  encodes the position and orientation of the limbs.	图1中，上图：多人姿势估计。属于同一个人的身体部位是相连的。 左下角：对应于连接右肘和右腕的肢体的部分关联区域（PAFs）。颜色编码方向。 右下角：放大了预测的PAFs。在场中的每个像素处，2D向量对肢体的位置和方向进行编码。
A common approach [23, 9, 27, 12, 19] is to employ  a person detector and perform single-person pose estimation  for each detection. These top-down approaches directly  leverage existing techniques for single-person pose  estimation [17, 31, 18, 28, 29, 7, 30, 5, 6, 20], but suffer  from early commitment: if the person detector fails–as it  is prone to do when people are in close proximity–there is  no recourse to recovery. Furthermore, the runtime of these top-down approaches is proportional to the number of people:  for each detection, a single-person pose estimator is  run, and the more people there are, the greater the computational  cost. In contrast, bottom-up approaches are attractive  as they offer robustness to early commitment and have the  potential to decouple runtime complexity from the number  of people in the image. Yet, bottom-up approaches do not  directly use global contextual cues from other body parts  and other people. In practice, previous bottom-up methods  [22, 11] do not retain the gains in efficiency as the final  parse requires costly global inference. For example, the  seminal work of Pishchulin et al. [22] proposed a bottom-up  approach that jointly labeled part detection candidates and  associated them to individual people. However, solving the  integer linear programming problem over a fully connected  graph is an NP-hard problem and the average processing  time is on the order of hours. Insafutdinov et al. [11] built  on [22] with stronger part detectors based on ResNet [10]  and image-dependent pairwise scores, and vastly improved  the runtime, but the method still takes several minutes per  image, with a limit on the number of part proposals. The  pairwise representations used in [11], are difficult to regress  precisely and thus a separate logistic regression is required.	一种常见的方法[23,9,27,12,19]是使用一个人检测器，对每个检测进行单人姿态估计。这些自顶向下的方法直接利用了现有的单人姿态估计技术[17、31、18、28、29、7、30、5、6、20]，但是早期的承诺有问题:如果人员检测器失败——当人们接近时很容易失败——就无法恢复。此外，这些自顶向下方法的运行时间与人员数量成正比:对于每个检测，运行一个单人姿态估计器，人员越多，计算成本越大。 相反，自底向上的方法很有吸引力，因为它们提供了对早期承诺的健壮性，并且有潜力将运行时复杂性与映像中的人员数量解耦。然而，自底向上的方法并不直接使用来自其他身体部位和其他人的全局上下文线索。在实践中，以前的自底向上方法[22,11]没有保留效率的提高，因为最后的解析需要昂贵的全局推理。例如，Pishchulin等人的开创性工作[22]提出了一种自底向上的方法，该方法联合标记部分检测候选对象并将它们与个人关联。然而，在全连通图上求解整数线性规划问题是一个np困难的问题，平均处理时间约为小时。Insafutdinov等人在[22]的基础上构建了更强大的基于ResNet[10]和图像相关的成对分数的部分检测器，并极大地改进了运行时间，但该方法仍然需要几分钟的图像，并限制了部分建议的数量。[11]中使用的成对表示很难精确地回归，因此需要单独的逻辑回归。
Figure 2. Overall pipeline. Our method takes the entire image as the input for a two-branch CNN to jointly predict confidence maps for  body part detection, shown in (b), and part affinity fields for parts association, shown in (c). The parsing step performs a set of bipartite  matchings to associate body parts candidates (d). We finally assemble them into full body poses for all people in the image (e).	图2。整体的流程。我们的方法将整个图像作为输入的两个分支CNN联合预测置信地图部位检测,(b)所示,部分协会和部分关联字段,(c)所示。解析步骤执行一组关联配合双方的身体部分候选(d)。我们终于将它们组装成完整的身体姿势对图像中所有人(e)。
In this paper, we present an efficient method for multiperson  pose estimation with state-of-the-art accuracy on  multiple public benchmarks. We present the first bottom-up  representation of association scores via Part Affinity Fields  (PAFs), a set of 2D vector fields that encode the location  and orientation of limbs over the image domain. We demonstrate  that simultaneously inferring these bottom-up representations  of detection and association encode global context  sufficiently well to allow a greedy parse to achieve  high-quality results, at a fraction of the computational cost.  We have publically released the code for full reproducibility,  presenting the first realtime system for multi-person 2D  pose detection.	在这篇论文中，我们提出了一种有效的方法，可以在多个公共基准上获得最精确的多姿态估计。我们提出了第一个自底向上表示的关联分数通过Part Affinity Fields (PAFs)，一组二维向量场编码的位置和方向的四肢在图像域。我们证明了同时推断这些自底向上的检测和关联表示可以很好地编码全局上下文，从而允许贪婪解析以一小部分计算成本获得高质量的结果。我们已经公开发布了代码的充分再现，提出了第一个实时系统的多个人2D位姿检测。

 

 

2. Method

Fig. 2 illustrates the overall pipeline of our method. The  system takes, as input, a color image of size w × h (Fig. 2a)  and produces, as output, the 2D locations of anatomical keypoints  for each person in the image (Fig. 2e). First, a feedforward  network simultaneously predicts a set of 2D confidence  maps S of body part locations (Fig. 2b) and a set  of 2D vector fields L of part affinities, which encode the  degree of association between parts (Fig. 2c). The set S =  (S1, S2, ..., SJ ) has J confidence maps, one per part, where  Sj ∈ Rw×h  , j ∈ {1 . . . J}. The set L = (L1,L2, ...,LC )  has C vector fields, one per limb1  , where Lc ∈ Rw×h×2  ,  c ∈ {1 . . . C}, each image location in Lc encodes a 2D vector  (as shown in Fig. 1). Finally, the confidence maps and  the affinity fields are parsed by greedy inference (Fig. 2d)  to output the 2D keypoints for all people in the image.

图2展示了我们的方法的总体流程。该系统将大小为w×h的彩色图像作为输入(图2a)，并将图像中每个人的二维解剖关键点位置作为输出(图2e)。首先，前馈网络同时预测一组二维人体部位置信度图S(图2b)和一组二维向量场L(图2c)，后者对人体部位之间的关联度进行编码。集合S = (S1, S2，…其中，SJ∈Rw×h, J∈{1…J}。集合L = (L1,L2，…，LC)有C个向量场，每个limb1一个，其中LC∈Rw×h×2,C∈{1…C}， Lc中的每个图像位置编码一个二维向量(如图1所示)，最后通过贪婪推理(图2D)解析置信图和亲和域，输出图像中所有人的二维关键点。

 

2.1. Simultaneous Detection and Association  

Our architecture, shown in Fig. 3, simultaneously predicts  detection confidence maps and affinity fields that encode  part-to-part association. The network is split into two  branches: the top branch, shown in beige, predicts the confidence  maps, and the bottom branch, shown in blue, predicts  the affinity fields. Each branch is an iterative prediction architecture, following Wei et al. [31], which refines  the predictions over successive stages, t ∈ {1, . . . , T}, with  intermediate supervision at each stage.	我们的架构，如图3所示，同时预测检测置信映射和编码部分到部分关联的关联字段。该网络分为两个分支：顶部分支（以米色显示）预测置信图，底部分支（以蓝色显示）预测关联字段。每个分支都是一个迭代预测体系结构，遵循Wei等人[31]改进了连续阶段的预测，t∈{1。. . ，T}，每个阶段都有中间监督。
The image is first analyzed by a convolutional network  (initialized by the first 10 layers of VGG-19 [26] and finetuned),  generating a set of feature maps F that is input to  the first stage of each branch. At the first stage, the network  produces a set of detection confidence maps S  1 = ρ  1  (F)  and a set of part affinity fields L  1 = φ  1  (F), where ρ  1  and  φ  1  are the CNNs for inference at Stage 1. In each subsequent  stage, the predictions from both branches in the previous  stage, along with the original image features F, are  concatenated and used to produce refined predictions	图像首先由卷积网络（由VGG-19的前10层初始化并微调）进行分析，生成一组输入到每个分支的第一级的特征映射F。在第一阶段，该网络产生一组检测置信映射S 1＝ρ1（F）和一组部分部件关联场l1＝φ1（F），其中ρ1和φ1是在第1阶段进行推断的CNNs。在随后的每个阶段中，将前一阶段中来自两个分支的预测与原始图像特征F连接起来，并用于生成精确的预测
Figure 4. Confidence maps of the right wrist (first row) and PAFs  (second row) of right forearm across stages. Although there is confusion  between left and right body parts and limbs in early stages,  the estimates are increasingly refined through global inference in  later stages, as shown in the highlighted areas.	图4 右腕（第一排）和右前臂（第二排）跨级的置信度图。尽管早期左右身体部位和四肢之间存在混淆，但在后期通过全局推断，估计值会越来越精确，如突出显示的区域所示。
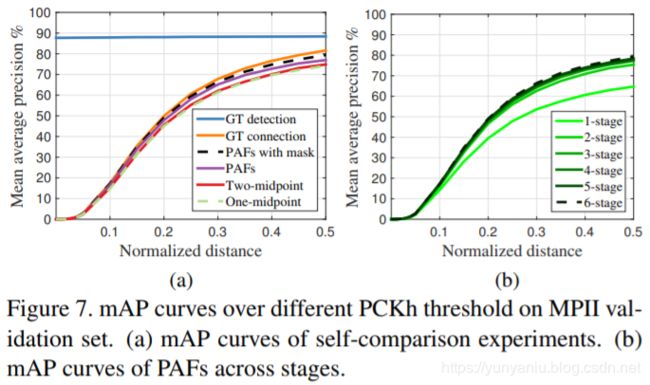
Fig. 4 shows the refinement of the confidence maps and  affinity fields across stages. To guide the network to iteratively  predict confidence maps of body parts in the first  branch and PAFs in the second branch, we apply two loss  functions at the end of each stage, one at each branch respectively.  We use an L2 loss between the estimated predictions  and the groundtruth maps and fields. Here, we weight  the loss functions spatially to address a practical issue that some datasets do not completely label all people. Specifically,  the loss functions at both branches at stage t are: where S  ∗  j  is the groundtruth part confidence map, L  ∗  c  is the  groundtruth part affinity vector field, W is a binary mask  with W(p) = 0 when the annotation is missing at an image  location p. The mask is used to avoid penalizing the  true positive predictions during training. The intermediate  supervision at each stage addresses the vanishing gradient  problem by replenishing the gradient periodically [31]. The  overall objective is	图4示出了跨阶段的置信映射和亲和域的细化。为了指导网络迭代预测第一分支和第二分支的身体部位的置信度图，我们在每个阶段的末尾分别应用两个损失函数，每个分支一个。我们在估计的预测和标定真值图和场之间使用L2损失。在这里，我们对损失函数进行空间加权，以解决一些数据集不能完全标记所有人的实际问题。具体来说，t阶段两个分支的损失函数为：

 

2.2. Confidence Maps for Part Detection

To evaluate fS in Eq. (5) during training, we generate  the groundtruth confidence maps S  ∗  from the annotated 2D  keypoints. Each confidence map is a 2D representation of  the belief that a particular body part occurs at each pixel  location. Ideally, if a single person occurs in the image,  a single peak should exist in each confidence map if the  corresponding part is visible; if multiple people occur, there  should be a peak corresponding to each visible part j for  each person k.
We first generate individual confidence maps S  ∗  j,k for  each person k. Let xj,k ∈ R2 be the groundtruth position of  body part j for person k in the image. The value at location  p ∈ R2  in S  ∗  j,k is defined as, where σ controls the spread of the peak. The groundtruth  confidence map to be predicted by the network is an aggregation  of the individual confidence maps via a max operator,
We take the maximum of  the confidence maps instead  of the average so that the  precision of close by peaks  remains distinct, as illustrated  in the right figure. At test time, we predict confidence  maps (as shown in the first row of Fig. 4), and obtain body  part candidates by performing non-maximum suppression.

 

2.3. Part Affinity Fields for Part Association  

Given a set of detected body parts (shown as the red and  blue points in Fig. 5a), how do we assemble them to form  the full-body poses of an unknown number of people? We  need a confidence measure of the association for each pair  of body part detections, i.e., that they belong to the same  person. One possible way to measure the association is to  detect an additional midpoint between each pair of parts  on a limb, and check for its incidence between candidate  part detections, as shown in Fig. 5b. However, when people  crowd together—as they are prone to do—these midpoints  are likely to support false associations (shown as green lines  in Fig. 5b). Such false associations arise due to two limitations  in the representation: (1) it encodes only the position,  and not the orientation, of each limb; (2) it reduces the region  of support of a limb to a single point.
To address these limitations, we present a novel feature  representation called part affinity fields that preserves both  location and orientation information across the region of  support of the limb (as shown in Fig. 5c). The part affinity  is a 2D vector field for each limb, also shown in Fig. 1d:  for each pixel in the area belonging to a particular limb, a 2D vector encodes the direction that points from one part of  the limb to the other. Each type of limb has a corresponding  affinity field joining its two associated body parts.
Consider a single limb shown in the figure below. Let  xj1,k and xj2,k be the groundtruth positions of body parts j1  and j2 from the limb c for person k in the image. If a point  0  0.1  0.2  0.3  0.4  0.5  0.6  0.7  0.8  0.9  1  Gaussian 1  Gaussian 2  Max  Average  p  S  0  0.2  0.4  0.6  0.8  1  Gaussian 1  Gaussian 2  Max  Average S  p  p  v  v?  p  xj2,1  xj1,k  xj2,k  p lies on the limb, the value  at L  ∗  c,k(p) is a unit vector  that points from j1 to j2; for  all other points, the vector is  zero-valued.
To evaluate fL in Eq. 5 during training, we define the  groundtruth part affinity vector field, L  ∗  c,k, at an image point  p as  L ∗ c,k(p) = ( v if p on limb c, k 0 otherwise. (8) Here, v = (xj2,k − xj1,k)/||xj2,k −xj1,k||2 is the unit vector in the direction of the limb. The set of points on the limb is defined as those within a distance threshold of the line segment, i.e., those points p for which  0 ≤ v · (p − xj1,k) ≤ lc,k and |v⊥ · (p − xj1,k)| ≤ σl where the limb width σl is a distance in pixels, the limb length is lc,k = ||xj2,k − xj1,k||2, and v⊥ is a vector perpendicular to v. The groundtruth part affinity field averages the affinity fields of all people in the image, L ∗ c (p) = 1 nc(p) X k L ∗ c,k(p), (9) where nc(p) is the number of non-zero vectors at point p across all k people (i.e., the average at pixels where limbs of different people overlap).
During testing, we measure association between candidate part detections by computing the line integral over the corresponding PAF, along the line segment connecting the candidate part locations. In other words, we measure the alignment of the predicted PAF with the candidate limb that would be formed by connecting the detected body parts. Specifically, for two candidate part locations dj1 and dj2 , we sample the predicted part affinity field, Lc along the line segment to measure the confidence in their association: where p(u) interpolates the position of the two body parts dj1 and dj2 , E = Z u=1 u=0 Lc (p(u)) · dj2 − dj1 ||dj2 − dj1 ||2 du, (10) In practice, we approximate the integral by sampling and summing uniformly-spaced values of u. p(u) = (1 − u)dj1 + udj2 . (11)
Figure 6. Graph matching. (a) Original image with part detections (b) K-partite graph (c) Tree structure (d) A set of bipartite graphs

 

2.4. Multi-Person Parsing using PAFs

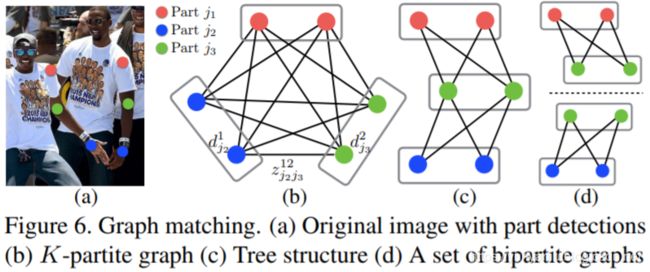
We perform non-maximum suppression on the detection confidence maps to obtain a discrete set of part candidate locations. For each part, we may have several candidates, due to multiple people in the image or false positives (shown in Fig. 6b). These part candidates define a large set of possible limbs. We score each candidate limb using the line integral computation on the PAF, defined in Eq. 10. The problem of finding the optimal parse corresponds to a K-dimensional matching problem that is known to be NP-Hard [32] (shown in Fig. 6c). In this paper, we present a greedy relaxation that consistently produces high-quality matches. We speculate the reason is that the pair-wise association scores implicitly encode global context, due to the large receptive field of the PAF network.
Formally, we first obtain a set of body part detection candidates DJ for multiple people, where DJ = {d m j : for j ∈ {1 . . . J}, m ∈ {1 . . . Nj}}, with Nj the number of candidates of part j, and d m j ∈ R2 is the location of the m-th detection candidate of body part j. These part detection candidates still need to be associated with other parts from the same person—in other words, we need to find the pairs of part detections that are in fact connected limbs. We define a variable z mn j1j2 ∈ {0, 1} to indicate whether two detection candidates d m j1 and d n j2 are connected, and the goal is to find the optimal assignment for the set of all possible connections, Z = {z mn j1j2 : for j1, j2 ∈ {1 . . . J}, m ∈ {1 . . . Nj1 }, n ∈ {1 . . . Nj2 }}.
If we consider a single pair of parts j1 and j2 (e.g., neck and right hip) for the c-th limb, finding the optimal association reduces to a maximum weight bipartite graph matching problem [32]. This case is shown in Fig. 5b. In this graph matching problem, nodes of the graph are the body part detection candidates Dj1 and Dj2 , and the edges are all possible connections between pairs of detection candidates. Additionally, each edge is weighted by Eq. 10—the part affinity aggregate. A matching in a bipartite graph is a subset of the edges chosen in such a way that no two edges share a node. Our goal is to find a matching with maximum weight for the chosen edges max Zc Ec = max Zc X m∈Dj1 X n∈Dj2 Emn · z mn j1j2 , (12) s.t. ∀m ∈ Dj1 , X n∈Dj2 z mn j1j2 ≤ 1, (13) ∀n ∈ Dj2 , X m∈Dj1 z mn j1j2 ≤ 1, (14) where Ec is the overall weight of the matching from limb type c, Zc is the subset of Z for limb type c, Emn is the part affinity between parts d m j1 and d n j2 defined in Eq. 10. Eqs. 13 and 14 enforce no two edges share a node, i.e., no two limbs of the same type (e.g., left forearm) share a part. We can use the Hungarian algorithm [14] to obtain the optimal matching.
When it comes to finding the full body pose of multiple people, determining Z is a K-dimensional matching problem. This problem is NP Hard [32] and many relaxations exist. In this work, we add two relaxations to the optimization, specialized to our domain. First, we choose a minimal number of edges to obtain a spanning tree skeleton of human pose rather than using the complete graph, as shown in Fig. 6c. Second, we further decompose the matching problem into a set of bipartite matching subproblems and determine the matching in adjacent tree nodes independently, as shown in Fig. 6d. We show detailed comparison results in Section 3.1, which demonstrate that minimal greedy inference well-approximate the global solution at a fraction of the computational cost. The reason is that the relationship between adjacent tree nodes is modeled explicitly by PAFs, but internally, the relationship between nonadjacent tree nodes is implicitly modeled by the CNN. This property emerges because the CNN is trained with a large receptive field, and PAFs from non-adjacent tree nodes also influence the predicted PAF.
With these two relaxations, the optimization is decomposed simply as: max Z E = X C c=1 max Zc Ec. (15) We therefore obtain the limb connection candidates for each limb type independently using Eqns. 12- 14. With all limb connection candidates, we can assemble the connections that share the same part detection candidates into full-body poses of multiple people. Our optimization scheme over the tree structure is orders of magnitude faster than the optimization over the fully connected graph [22, 11].

 

3. Results

We evaluate our method on two benchmarks for multiperson pose estimation: (1) the MPII human multi-person dataset [2] and (2) the COCO 2016 keypoints challenge dataset [15]. These two datasets collect images in diverse scenarios that contain many real-world challenges such as crowding, scale variation, occlusion, and contact. Our approach set the state-of-the-art on the inaugural COCO 2016 keypoints challenge [1], and significantly exceeds the previous state-of-the-art result on the MPII multi-person benchmark. We also provide runtime analysis to quantify the efficiency of the system. Fig. 10 shows some qualitative results from our algorithm.

 

3.1. Results on the MPII Multi-Person Dataset

For comparison on the MPII dataset, we use the toolkit [22] to measure mean Average Precision (mAP) of all body parts based on the PCKh threshold. Table 1 compares mAP performance between our method and other approaches on the same subset of 288 testing images as in [22], and the entire MPI testing set, and self-comparison on our own validation set. Besides these measures, we compare the average inference/optimization time per image in seconds. For the 288 images subset, our method outperforms previous state-of-the-art bottom-up methods [11] by 8.5% mAP. Remarkably, our inference time is 6 orders of magnitude less. We report a more detailed runtime analysis in Section 3.3. For the entire MPII testing set, our method without scale search already outperforms previous state-of-the-art methods by a large margin, i.e., 13% absolute increase on mAP. Using a 3 scale search (×0.7, ×1 and ×1.3) further increases the performance to 75.6% mAP. The mAP comparison with previous bottom-up approaches indicate the effectiveness of our novel feature representation, PAFs, to associate body parts. Based on the tree structure, our greedy parsing method achieves better accuracy than a graphcut optimization formula based on a fully connected graph structure [22, 11].
In Table 2, we show comparison results on different skeleton structures as shown in Fig. 6 on our validation set, i.e., 343 images excluded from the MPII training set. We train our model based on a fully connected graph, and compare results by selecting all edges (Fig. 6b, approximately solved by Integer Linear Programming), and minimal tree edges (Fig. 6c, approximately solved by Integer Linear Pro-gramming, and Fig. 6d, solved by the greedy algorithm presented in this paper). Their similar performance shows that it suffices to use minimal edges. We trained another model that only learns the minimal edges to fully utilize the network capacity—the method presented in this paper—that is denoted as Fig. 6d (sep). This approach outperforms Fig. 6c and even Fig. 6b, while maintaining efficiency. The reason is that the much smaller number of part association channels (13 edges of a tree vs 91 edges of a graph) makes it easier for training convergence.
Figure 7. mAP curves over different PCKh threshold on MPII validation  set. (a) mAP curves of self-comparison experiments. (b)  mAP curves of PAFs across stages.
Fig. 7a shows an ablation analysis on our validation set. For the threshold of PCKh-0.5, the result using PAFs outperforms the results using the midpoint representation, specifically, it is 2.9% higher than one-midpoint and 2.3% higher than two intermediate points. The PAFs, which encodes both position and orientation information of human limbs, is better able to distinguish the common cross-over cases, e.g., overlapping arms. Training with masks of unlabeled persons further improves the performance by 2.3% because it avoids penalizing the true positive prediction in the loss during training. If we use the ground-truth keypoint location with our parsing algorithm, we can obtain a mAP of 88.3%. In Fig. 7a, the mAP of our parsing with GT detection is constant across different PCKh thresholds due to no localization error. Using GT connection with our keypoint detection achieves a mAP of 81.6%. It is notable that our parsing algorithm based on PAFs achieves a similar mAP as using GT connections (79.4% vs 81.6%). This indicates parsing based on PAFs is quite robust in associating correct part detections. Fig. 7b shows a comparison of performance across stages. The mAP increases monotonically with the iterative refinement framework. Fig. 4 shows the qualitative improvement of the predictions over stages.

 

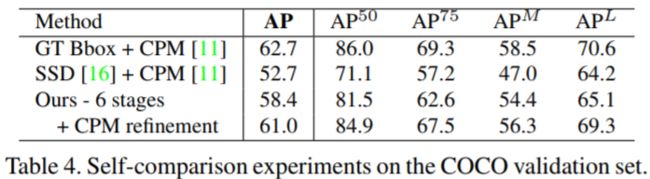
3.2. Results on the COCO Keypoints Challenge

Table 3. Results on the COCO 2016 keypoint challenge. Top: results on test-challenge. Bottom: results on test-dev (top methods only). AP50 is for OKS = 0.5, APL is for large scale persons.
The COCO training set consists of over 100K person instances labeled with over 1 million total keypoints (i.e. body parts). The testing set contains “test-challenge”, “test-dev” and “test-standard” subsets, which have roughly 20K images each. The COCO evaluation defines the object key point similarity (OKS) and uses the mean average precision (AP) over 10 OKS thresholds as main competition metric [1]. The OKS plays the same role as the IoU in object detection. It is calculated from scale of the person and the distance between predicted points and GT points. Table 3 shows results from top teams in the challenge. It is noteworthy that our method has lower accuracy than the top-down methods on people of smaller scales (APM). The reason is that our method has to deal with a much larger scale range spanned by all people in the image in one shot. In contrast, top-down methods can rescale the patch of each detected area to a larger size and thus suffer less degradation at smaller scales.
In Table 4, we report self-comparisons on a subset of the COCO validation set, i.e., 1160 images that are randomly selected. If we use the GT bounding box and a single person CPM [31], we can achieve a upper-bound for the top-down approach using CPM, which is 62.7% AP. If we use the state-of-the-art object detector, Single Shot MultiBox Detector (SSD)[16], the performance drops 10%. This comparison indicates the performance of top-down approaches rely heavily on the person detector. In contrast, our bottom-up method achieves 58.4% AP. If we refine the results of our method by applying a single person CPM on each rescaled region of the estimated persons parsed by our method, we gain an 2.6% overall AP increase. Note that we only update estimations on predictions that both methods agree well enough, resulting in improved precision and recall. We expect a larger scale search can further improve the performance of our bottom-up method. Fig. 8 shows a breakdown of errors of our method on the COCO validation set. Most of the false positives come from imprecise localization, other than background confusion. This indicates there is more improvement space in capturing spatial dependencies than in recognizing body parts appearances.

 

3.3. Runtime Analysis

To analyze the runtime performance of our method, we collect videos with a varying number of people. The original frame size is 1080×1920, which we resize to 368×654 during testing to fit in GPU memory. The runtime analysis is performed on a laptop with one NVIDIA GeForce GTX-1080 GPU. In Fig. 8d, we use person detection and single-person CPM as a top-down comparison, where the runtime is roughly proportional to the number of people in the image. In contrast, the runtime of our bottom-up approach increases relatively slowly with the increasing number of people. The runtime consists of two major parts: (1) CNN processing time whose runtime complexity is O(1), constant with varying number of people; (2) Multi-person parsing time whose runtime complexity is O(n 2 ), where n represents the number of people. However, the parsing time does not significantly influence the overall runtime because it is two orders of magnitude less than the CNN processing time, e.g., for 9 people, the parsing takes 0.58 ms while CNN takes 99.6 ms. Our method has achieved the speed of 8.8 fps for a video with 19 people.

 

 

4. Discussion

Moments of social significance, more than anything else, compel people to produce photographs and videos. Our photo collections tend to capture moments of personal significance: birthdays, weddings, vacations, pilgrimages, sports events, graduations, family portraits, and so on. To enable machines to interpret the significance of such photographs, they need to have an understanding of people in images. Machines, endowed with such perception in real time, would be able to react to and even participate in the individual and social behavior of people. In this paper, we consider a critical component of such perception: realtime algorithms to detect the 2D pose of multiple people in images. We present an explicit nonparametric representation of the keypoints association that encodes both position and orientation of human limbs. Second, we design an architecture for jointly learning parts detection and parts association. Third, we demonstrate that a greedy parsing algorithm is sufficient to produce highquality parses of body poses, that maintains efficiency even as the number of people in the image increases. We show representative failure cases in Fig. 9. We have publicly released our code (including the trained models) to ensure full reproducibility and to encourage future research in the area.

 

Acknowledgements

We acknowledge the effort from the authors of the MPII and COCO human pose datasets. These datasets make 2D human pose estimation in the wild possible. This research was supported in part by ONR Grants N00014-15-1-2358 and N00014-14-1-0595.

 

 

References

[1] MSCOCO keypoint evaluation metric. http://mscoco. org/dataset/#keypoints-eval. 5, 6‌
[2] M. Andriluka, L. Pishchulin, P. Gehler, and B. Schiele. 2D human pose estimation: new benchmark and state of the art analysis. In CVPR, 2014. 5
[3] M. Andriluka, S. Roth, and B. Schiele. Pictorial structures revisited: people detection and articulated pose estimation. In CVPR, 2009. 1
[4] M. Andriluka, S. Roth, and B. Schiele. Monocular 3D pose estimation and tracking by detection. In CVPR, 2010. 1‌
[5] V. Belagiannis and A. Zisserman. Recurrent human pose es- timation. In 12th IEEE International Conference and Work- shops on Automatic Face and Gesture Recognition (FG), 2017. 1
[6] A. Bulat and G. Tzimiropoulos. Human pose estimation via convolutional part heatmap regression. In ECCV, 2016. 1
[7] X. Chen and A. Yuille. Articulated pose estimation by a graphical model with image dependent pairwise relations. In NIPS, 2014. 1
[8] P. F. Felzenszwalb and D. P. Huttenlocher. Pictorial struc- tures for object recognition. In IJCV, 2005. 1
[9] G. Gkioxari, B. Hariharan, R. Girshick, and J. Malik. Us- ing k-poselets for detecting people and localizing their key- points. In CVPR, 2014. 1
[10] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In CVPR, 2016. 1
[11] E. Insafutdinov, L. Pishchulin, B. Andres, M. Andriluka, and
B. Schiele. Deepercut: A deeper, stronger, and faster multi- person pose estimation model. In ECCV, 2016. 1, 5, 6
[12] U. Iqbal and J. Gall. Multi-person pose estimation with local joint-to-person associations. In ECCV Workshops, Crowd Understanding, 2016. 1, 5
[13] S. Johnson and M. Everingham. Clustered pose and nonlin- ear appearance models for human pose estimation. In BMVC, 2010. 1
[14] H. W. Kuhn. The hungarian method for the assignment prob- lem. In Naval research logistics quarterly. Wiley Online Li- brary, 1955. 5
[15] T.-Y. Lin, M. Maire, S. Belongie, J. Hays, P. Perona, D. Ra- manan, P. Dolla´r, and C. L. Zitnick. Microsoft COCO: com- mon objects in context. In ECCV, 2014. 5
[16] W. Liu, D. Anguelov, D. Erhan, C. Szegedy, and S. Reed.
Ssd: Single shot multibox detector. In ECCV, 2016. 6
[17] A. Newell, K. Yang, and J. Deng. Stacked hourglass net- works for human pose estimation. In ECCV, 2016. 1
[18] W. Ouyang, X. Chu, and X. Wang. Multi-source deep learn- ing for human pose estimation. In CVPR, 2014. 1
[19] G. Papandreou, T. Zhu, N. Kanazawa, A. Toshev, J. Tomp- son, C. Bregler, and K. Murphy. Towards accurate multi-person pose estimation in the wild. arXiv preprint arXiv:1701.01779, 2017. 1, 6
[20] T. Pfister, J. Charles, and A. Zisserman. Flowing convnets for human pose estimation in videos. In ICCV, 2015. 1
[21] L. Pishchulin, M. Andriluka, P. Gehler, and B. Schiele. Pose- let conditioned pictorial structures. In CVPR, 2013. 1
[22] L. Pishchulin, E. Insafutdinov, S. Tang, B. Andres, M. An- driluka, P. Gehler, and B. Schiele. Deepcut: Joint subset partition and labeling for multi person pose estimation. In CVPR, 2016. 1, 5
[23] L. Pishchulin, A. Jain, M. Andriluka, T. Thorma¨hlen, and
B. Schiele. Articulated people detection and pose estimation:
Reshaping the future. In CVPR, 2012. 1
[24] V. Ramakrishna, D. Munoz, M. Hebert, J. A. Bagnell, and
Y. Sheikh. Pose machines: Articulated pose estimation via inference machines. In ECCV, 2014. 1
[25] D. Ramanan, D. A. Forsyth, and A. Zisserman. Strike a Pose: Tracking people by finding stylized poses. In CVPR, 2005. 1‌
[26] K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition. In ICLR, 2015. 2
[27] M. Sun and S. Savarese. Articulated part-based model for joint object detection and pose estimation. In ICCV, 2011. 1
[28] J. Tompson, R. Goroshin, A. Jain, Y. LeCun, and C. Bregler.
Efficient object localization using convolutional networks. In
CVPR, 2015. 1
[29] J. J. Tompson, A. Jain, Y. LeCun, and C. Bregler. Joint train- ing of a convolutional network and a graphical model for human pose estimation. In NIPS, 2014. 1
[30] A. Toshev and C. Szegedy. Deeppose: Human pose estima- tion via deep neural networks. In CVPR, 2014. 1
[31] S.-E. Wei, V. Ramakrishna, T. Kanade, and Y. Sheikh. Con- volutional pose machines. In CVPR, 2016. 1, 2, 3, 6
[32] D. B. West et al. Introduction to graph theory, volume 2.
Prentice hall Upper Saddle River, 2001. 4, 5
[33] Y. Yang and D. Ramanan. Articulated human detection with flexible mixtures of parts. In TPAMI, 2013. 1