线性系统实验:化学方程式配平 与 天体轨道参数估计
线性系统
- 消元法
- 高斯消元法
- 高斯-约旦消元法
- 工程应用:化学方程式配平
- 逆矩阵求解
- 矩阵的逆
- 解的结构
- 超定方程组近似估值
- 工程应用:天体轨道参数估计
消元法
线性系统,在高中称为 多元一次方程组,因为在线性代数里,我们把矩阵看成系统,而这些方程组的未知数都只有一次,所以就了线性系统。
- { 1 x + 2 y = 5 3 x + 4 y = 6 \left\{\begin{matrix} 1x + 2y = 5 & \\ 3x + 4y = 6 & \end{matrix}\right. {1x+2y=53x+4y=6
我们把真实世界的问题,转换为线性方程(线性系统),研究线性系统,也就是解这些方程,解出来问题就解决了。
高斯消元法
初中的时候,我们学习了高斯消元法。
高斯消元法主要分为两步,
- 消元:要减少某些方程中元的数量;
- 回代:是把已知的解代入到方程式中,求出其他未知的解。
如果方程和元的数量很小,那么高斯消元法并不难理解。
可是如果方程和元的数量很多,整个过程就变得比较繁琐了。
而后,自然而然人们想到了对计算进行批处理,可以把高斯消元法转为矩阵的操作。
比如:
- { 1 x + 2 y + 4 z = 7 3 x + 7 y + 2 z = − 11 2 x + 3 y + 3 z = 1 \left\{\begin{matrix} 1x + 2y + 4z = 7 ~~~~\\ ~3x + 7y + 2z = -11\\ 2x + 3y + 3z = 1~~~~\\ \end{matrix}\right. ⎩⎨⎧1x+2y+4z=7 3x+7y+2z=−112x+3y+3z=1
用矩阵表示(矩阵乘法):
- [ 1 2 4 3 7 2 2 3 3 ] ∗ [ x y z ] = [ 7 − 11 1 ] \left[ \begin{matrix} 1 & 2 & 4 \\ 3 & 7 & 2 \\ 2 & 3 & 3 \end{matrix} \right]*\left[ \begin{matrix} x\\ y\\ z \end{matrix} \right]=\left[ \begin{matrix} 7\\ -11\\ 1 \end{matrix} \right] ⎣⎡132273423⎦⎤∗⎣⎡xyz⎦⎤=⎣⎡7−111⎦⎤
我们再把系数矩阵和等式右边的矩阵放在一起:
- { 1 2 4 7 3 7 2 − 11 2 3 3 1 } \left\{ \begin{array}{ccc|c} 1 & 2 & 4 &7 \\ 3 & 7 & 2 & -11 \\ 2 & 3 & 3 & 1 \end{array} \right\} ⎩⎨⎧1322734237−111⎭⎬⎫
这个矩阵叫【增广矩阵】,就是在系数矩阵右边增加了一列等号右边的解。
通过矩阵解线性方程,本质也是消元法,要做的就是把消元的过程封装到矩阵里。
用消元法解方程,因为操作的是矩阵,所以消元法的书写方式有点变化:
- 原【一个方程的左右俩边同时乘以一个常数】 变为【矩阵的某一行乘以一个常数】
- 原【一个方程加(或减)另一个方程】 变为【矩阵的一行加(或减)另一行】
- 原【交换俩个方程的位置】 变为【交换矩阵的俩行】
也就是说,计算方式是完全一致的,只不过操作对象从方程变成了矩阵,因为矩阵是可以批处理运算的工具。
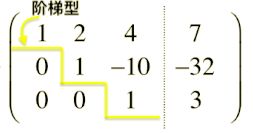
我快速手算一下:
-
从上到下,以矩阵的第一行为基准,消去第二、第三行的第一个元素(系数化为 0 0 0)
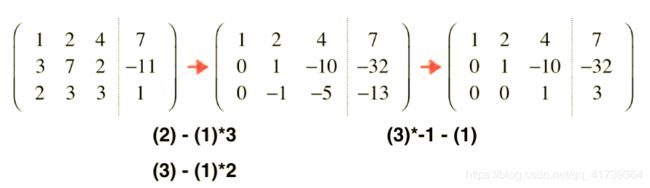
第一步 ( 2 ) − ( 1 ) ∗ 3 (2) - (1)*3 (2)−(1)∗3,把第二行的第一个元素化成 0 0 0;第二步 ( 3 ) − ( 1 ) ∗ 2 (3) - (1)*2 (3)−(1)∗2,把第三行的第一个元素化成 0 0 0;
第三步 ( 3 ) ∗ − 1 − ( 1 ) (3)*-1 - (1) (3)∗−1−(1),把第三行的第二个元素化成 0 0 0;
第三步后矩阵的第三行是 [ 0 0 − 15 45 ] \left[\begin{array}{ccc|c}0 & 0 & -15 & 45\\ \end{array} \right] [00−1545],而后给第三行左右俩边同时除以 − 15 -15 −15,最后的结果就是上图最后一个矩阵。
现在我们知道,最后一个未知数 z = 3 z=3 z=3,这是消元法的消元部分,接着是回代部分,由下往上回代解出其余未知数:)。
总结一下,高斯消元法。
消元部分:
-
从上到下,以矩阵的第一行为基准,消去第二、第三行的第一个元素(系数化为 0 0 0),这就代表消去了一个元;
因为他们都是基于矩阵第一行第一个位置消元的,所以这个位置也被称为【主元】。
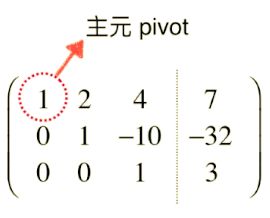
不仅第一行第一个位置是主元,第二行第二个、第三行第三个、第 n n n 行第 n n n个都是主元。P.S. 只要在这个位置,任何不为 0,就可以当主元。如果第一行第一个元素为 0 0 0,就需要【交换矩阵的俩行】。若第一行主元不为 1 1 1 的元素,先化为 1 1 1,再运算。
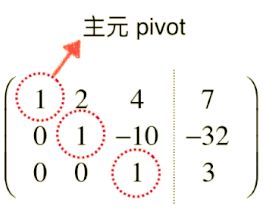
首先就是把这些主元位置的系数化为 1 1 1,之后其他行就可以使用 【矩阵的某一行乘以一个常数】、【矩阵的一行加(或减)另一行】把每行主元左边的元素化为 0 0 0。最后,矩阵会变成一个阶梯型的矩阵,比如这样。
回代部分:
- 由下往上回代解出其余未知数,把最后一个未知数代入倒数第二行,得到倒数第二个未知数的解;再把倒数第一、倒数第二的未知数代入到第一个里面,得到 3 3 3 个未知数的解。
高斯消元法实现:
// 运行:命令行输入 gcc/g++ 当前源文件.c/cpp
#include高斯消元法演示:
高斯-约旦消元法
高斯消元法的问题,只能通过矩阵得到最后一个未知数的解,之后还得一直回代依次得到所有结果,那有木有什么方法一次性把结果捣鼓出来呢?
有呀,高斯-约旦消元法。
回到高斯消元法的消元后,其实我们也可以不用回代,只有把 − 10 -10 −10 化为 0 0 0 即可。
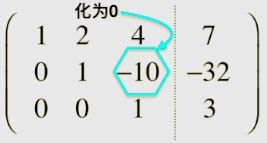
我们倒着进行消元即可,初始的消元是从第一行开始,从上往下以第一行的主元为基准,把主元下面的位置都化为 0 0 0,现在反过来从最后一行开始,从下往上以最后一行的主元为基准,把主元上面的位置都化为 0 0 0。
高斯-约旦消元法:
- 高斯消元:前向过程,从上到下
- 约旦消元:后向过程,从下到上
// 运行:在命令行输入 g++ -std=c++11 当前源文件.cpp
#include
工程应用:化学方程式配平
问题描述:给出一个未配平的化学方程式,根据质量守恒定律对其分配,不考虑化合价问题
示例:)
- 输入:Cu+HNO3=Cu(NO3)2+NO+H2O(中间不要加入空格)
- 输出:3Cu+8HNO3=3Cu(NO3)2+2NO+4H2O
分析:
化学反应遵循质量守恒定律,反应前后的原子种类和数量保持不变,根据这,采用【待定系数法】来配平化学方程式。
具体的操作,给方程式中的每一项设一个待定系数,列出方程组。
比如说,输入示例方程式,分别设 C u 、 H N O 3 、 C u ( N O 3 ) 2 、 N O 、 H 2 O C_{u}、HNO_{3}、Cu(NO_{3})2、NO、H_{2}O Cu、HNO3、Cu(NO3)2、NO、H2O 的系数为 x 1 、 x 2 、 x 3 、 x 4 、 x 5 x_{1}、x_{2}、x_{3}、x_{4}、x_{5} x1、x2、x3、x4、x5。
由元素 C u 、 H 、 N 、 O C_{u}、H、N、O Cu、H、N、O 的守恒,得到方程组:
- { x 1 = x 3 x 2 = 2 x 5 x 2 = 2 x 3 + x 4 3 x 2 = 6 x 3 + x 4 + x 5 \left\{\begin{matrix} x_{1} = x_{3}~~~~~~~~~~~~~~~~~~~~~ \\ x_{2} = 2x_{5}~~~~~~~~~~~~~~~~~~~ \\ x_{2} = 2x_{3}+x_{4} ~~~~~~~~~~~\\ 3x_{2} = 6x_{3}+x_{4}+x_{5} \end{matrix}\right. ⎩⎪⎪⎨⎪⎪⎧x1=x3 x2=2x5 x2=2x3+x4 3x2=6x3+x4+x5
但方程组只有 4 4 4 个方程,未知数却有 5 5 5 个,无法求出唯一确定的一组解。
因为化学方程式系数间只是一种比例关系,可令 x 5 = 1 x_{5}=1 x5=1,得:
- { x 1 = 3 4 x 2 = 2 x 3 = 3 4 x 4 = 1 2 \left\{\begin{matrix} x_{1} = \frac{3}{4} \\ x_{2} = 2 \\ x_{3} = \frac{3}{4} \\ x_{4} = \frac{1}{2} \end{matrix}\right. ⎩⎪⎪⎨⎪⎪⎧x1=43x2=2x3=43x4=21
各项系数都乘 4 4 4,得到最后的结果。
用计算机实现,应该用矩阵代替,消元法相同只是从操作方程变成了操作矩阵。
此外,还得将化学方程式转为线性方程组,难点在于去括号。
// 运行:在命令行输入 gcc 当前源文件.c
#include
逆矩阵求解
求解线性方程组除了消元法之外,逆矩阵也可求解。
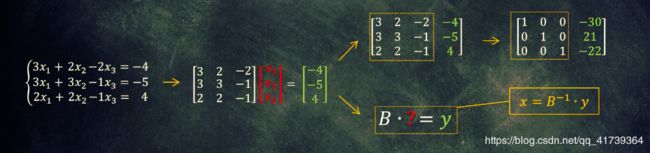
在《矩阵实验:图形图像处理》,着重写了把矩阵看成一种对向量的函数、变换。
上面的方程,从线性系统的角度来看线性方程组的求解过程:
- [ 3 2 − 2 3 3 − 1 2 2 − 1 ] ∗ [ x 1 x 2 x 3 ] = [ − 4 − 5 4 ] \begin{bmatrix} 3 &2 &-2 \\ 3& 3 &-1 \\ 2& 2 &-1 \end{bmatrix}*\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3} \end{bmatrix}=\begin{bmatrix} -4\\ -5\\ ~~4 \end{bmatrix} ⎣⎡332232−2−1−1⎦⎤∗⎣⎡x1x2x3⎦⎤=⎣⎡−4−5 4⎦⎤
线性系统相当于:
- B ∗ ? = y B~*~?=y B ∗ ?=y
上面的方程,从线性变换的角度来看线性方程组的求解过程:
- [ 3 2 − 2 3 3 − 1 2 2 − 1 ] ∗ [ − 30 21 − 22 ] = [ y 1 y 2 y 3 ] \begin{bmatrix} 3 &2 &-2 \\ 3& 3 &-1 \\ 2& 2 &-1 \end{bmatrix}* \begin{bmatrix} -30\\ ~~21\\ -22\end{bmatrix} =\begin{bmatrix} y_{1}\\ y_{2}\\ y_{3} \end{bmatrix} ⎣⎡332232−2−1−1⎦⎤∗⎣⎡−30 21−22⎦⎤=⎣⎡y1y2y3⎦⎤
线性变换相当于;
- B ∗ x = ? B*x=~? B∗x= ?,矩阵 B B B 是变换。
看线性系统,已知变换矩阵 B B B、输出矩阵 y y y,求解输入矩阵 x x x。
那求解线性方程组就是一个逆变换的过程;因此,有一个逆矩阵表征这种变换。
逆矩阵:若 A B = E AB=E AB=E ,则称 A , B A,~B A, B 互为逆矩阵;记作: B − 1 = A o r A − 1 = B B^{-1}=A ~~or~~A^{-1}=B B−1=A or A−1=B。
如果我们在等式俩边都乘,式子如下:
- E x = ( A B ) x = A ( B x ) = B − 1 ( B x ) Ex=(AB)x=A(Bx)=B^{-1}(Bx) Ex=(AB)x=A(Bx)=B−1(Bx)
这个式子在几何上,变换来变换去,最后回到初始状态:
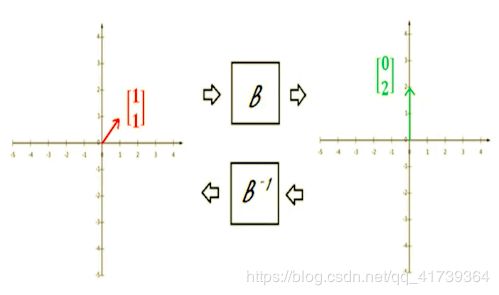
参照这种思想(矩阵是一种变换的思想), B ∗ ? = y B~*~?=y B ∗ ?=y 可以用 x = B − 1 ∗ y x=B^{-1}*y x=B−1∗y 来求!!
求线性方程组就变成了求解某个矩阵的逆矩阵。
现在,唯一要明白的是:逆矩阵怎么求 ?
矩阵的逆
除零以外,一个数字乘以这个数字的倒数(逆)等于一:
- x ∗ x − 1 = 1 x*x^{-1} = 1 x∗x−1=1
这是在数字系统里,事实上,矩阵也可以逆:
- A B = B A = I AB=BA=I AB=BA=I, I I I 是单位矩阵,相当于数字里面的 1 1 1。
如果矩阵满足上述 等 式 等式 等式,则称 B B B 是 A A A 的逆矩阵,记做: B = A − 1 B=A^{-1} B=A−1
大部分矩阵都是有逆的:
- 有逆的矩阵叫
可逆矩阵or非奇异矩阵 - 不可逆的矩阵叫
不可逆矩阵or奇异矩阵
因为矩阵乘法不满足交换律,所以可逆分成了俩种:
- 左逆: B A = I BA=I BA=I,只有左逆,是不可逆矩阵;
- 右逆: A B = I AB=I AB=I,只有右逆,是不可逆矩阵;
可逆矩阵是同时有左逆和右逆,只有左逆或只有右逆都不叫可逆。
- 只有方阵可逆(行数 = 列数),因为对于一个方阵来说,左逆和右逆一定是同时存在的。
本科的线性代数主要研究方阵(除了线性系统)。
矩阵求逆:
# 运行:在命令行里输入 python 当前源文件.py
import numpy as np
from scipy import linalg
A = np.array([[1, 35, 0],
[0, 2, 3],
[0, 0, 4]])
A_n = linalg.inv(A)
print(A_n)
print(np.dot(A, A_n))
运行结果:
[[ 1. -17.5 13.125]
[ 0. 0.5 -0.375]
[ 0. 0. 0.25 ]]
[[ 1. 0. 0.]
[ 0. 1. 0.]
[ 0. 0. 1.]]
C++ 也有专属的线代库 armadillo,因为有数据类型有精度限制可以用 Boost.Multiprecision,用于科学计算也就很方便。
解的结构
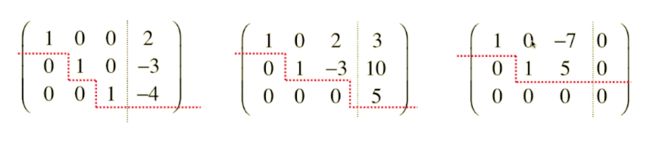
消元法所做的是把一个增广矩阵变换为一个阶梯型矩阵。
- 非零行第一个元素(主元)为 1 1 1
- 主元所在列的其他元素均为 0 0 0
满足这种条件的矩阵,也被称为 “行最简形式”。
线性方程组 通过 消元法 变成 行最简形式,这样就可以直接判断方程组解的情况:
- 适定方程组:方程组有唯一解,理想情况,遇到的情况不多;
- 超定方程组:方程组无解,无论三个未知数取什么解,方程始终不能满足,因此方程组无解;遇到的概率很大;
- 欠定方程组:方程组有无数解,这种方程组的未知数有无数个解,因此实用价值不大。
- 欠定方程组(无数解):系数矩阵的秩 = 增广矩阵的秩 < 未知数个数;
- 适定方程组(唯一解):系数矩阵的秩 = 增广矩阵的秩 = 未知数个数;
- 超定方程组(无 解):系数矩阵的秩 ≠ \neq = 增广矩阵的秩 。
超定方程组近似估值
我们遇到的多是 超定方程组,因此学习一下 如何求超定方程的近似解。
先看一个比较简单的问题。
设 → u = ( 1 , 1 ) T , → v = ( 2 , 0 ) T , → b = ( 3 , 1 ) T \underset{u}{\rightarrow}=(1,1)^{T},\underset{v}{\rightarrow}=(2,0)^{T},\underset{b}{\rightarrow}=(3,1)^{T} u→=(1,1)T,v→=(2,0)T,b→=(3,1)T,能否找到一组 x 1 , x 2 x_{1}, x_{2} x1,x2 满足: x 1 ∗ → u + x 2 ∗ → v = → b x_{1}*\underset{u}{\rightarrow}+x_{2}*\underset{v}{\rightarrow}=\underset{b}{\rightarrow} x1∗u→+x2∗v→=b→。
用矩阵表示: [ u , v ] ∗ [ x 1 x 2 ] = b \left [ u,v \right ]*\begin{bmatrix} x_{1}\\ x_{2} \end{bmatrix}=b [u,v]∗[x1x2]=b,也等同于 [ 1 2 1 0 ] ∗ [ x 1 x 2 ] = [ 3 1 ] \begin{bmatrix} 1 &2 \\ 1 & 0 \end{bmatrix}*\begin{bmatrix} x_{1}\\ x_{2} \end{bmatrix}=\begin{bmatrix} 3\\ 1 \end{bmatrix} [1120]∗[x1x2]=[31], (解出来是,适定方程组),解得(唯一解) : x 1 = 1 , x 2 = 1 x_{1}=1, x_{2}=1 x1=1,x2=1。
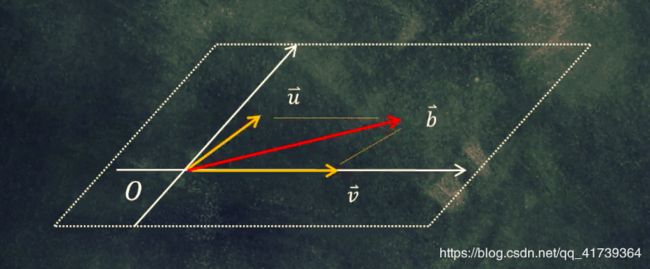
第二个问题,设 → u = ( 1 , 1 , 0 ) T , → v = ( 2 , 0 , 0 ) T , → b = ( 3 , 1 , 3 ) T \underset{u}{\rightarrow}=(1,1,0)^{T},\underset{v}{\rightarrow}=(2,0,0)^{T},\underset{b}{\rightarrow}=(3,1,3)^{T} u→=(1,1,0)T,v→=(2,0,0)T,b→=(3,1,3)T,试问,能否找到一组 x 1 , x 2 x_{1}, x_{2} x1,x2 满足: x 1 ∗ → u + x 2 ∗ → v = → b x_{1}*\underset{u}{\rightarrow}+x_{2}*\underset{v}{\rightarrow}=\underset{b}{\rightarrow} x1∗u→+x2∗v→=b→。
用矩阵表示: [ u , v ] ∗ [ x 1 x 2 ] = b \left [ u,v \right ]*\begin{bmatrix} x_{1}\\ x_{2} \end{bmatrix}=b [u,v]∗[x1x2]=b,也等同于 [ 1 2 1 0 0 0 ] ∗ [ x 1 x 2 ] = [ 3 1 3 ] \begin{bmatrix} 1 &2 \\ 1 &0 \\ 0 & 0 \end{bmatrix}*\begin{bmatrix} x_{1}\\ x_{2} \end{bmatrix}=\begin{bmatrix} 3\\ 1\\ 3 \end{bmatrix} ⎣⎡110200⎦⎤∗[x1x2]=⎣⎡313⎦⎤,(解出来是,超定方程组),无解。
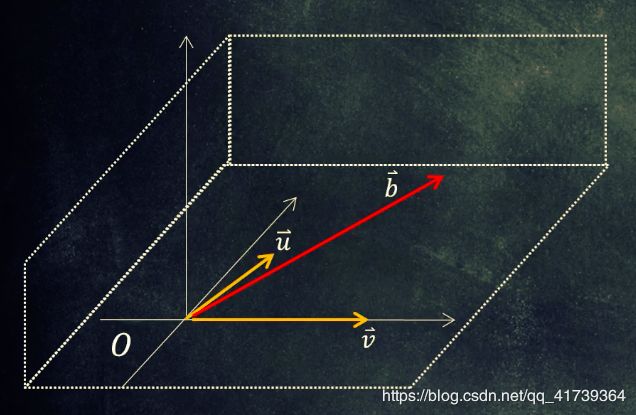
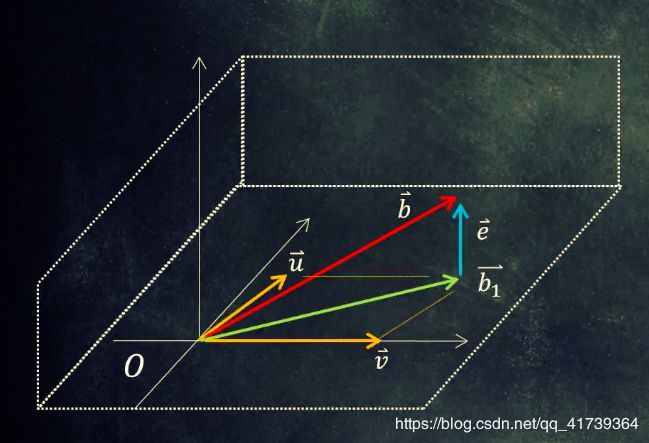
图中的向量 b b b,脱离了 u , v u~,v u ,v 俩个向量的平面;这就从几何上说满足条件的未知数是无法找到的。
虽然无解,但却可以找到一个最接近向量 b b b 的 b 1 b_{1} b1 向量 ,如下图。
b b b 向量 - b 1 b_{1} b1 向量 = e e e 向量
- 方程组表达式: A → x = → b A\underset{x}{\rightarrow}=\underset{b}{\rightarrow} Ax→=b→
- 在等式俩边都乘一个 A T : A T A → x = A T → b A^{T}:A^{T}A\underset{x}{\rightarrow}=A^{T}\underset{b}{\rightarrow} AT:ATAx→=ATb→
A A A 的转置乘 A A A 必然是一个实对称矩阵,实对称矩阵必定可逆,等式的左右俩边还可以乘 A A A 的转置: ( A T A ) − 1 A T → b (A^{T}A)^{-1}A^{T}\underset{b}{\rightarrow} (ATA)−1ATb→。
工程应用:天体轨道参数估计
前置知识:《极坐标、开普勒第一定律》。
根据开普勒第一定律,当忽略其他天体的重量吸引时,一个天体应该取椭圆、抛物线或双曲线轨道。
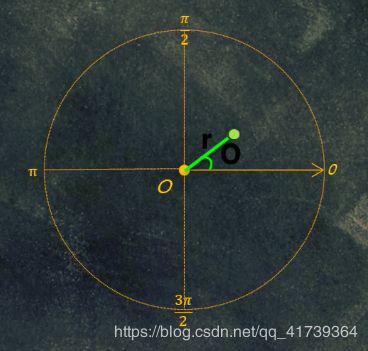
在极坐标 ( Θ , r ) (\Theta,~r) (Θ, r) 中,天体的位置满足一个方程:
- r = β + e ( r c o s ( Θ ) ) r = \beta + e(r~cos(\Theta)) r=β+e(r cos(Θ))
β \beta β 为轨道常数, e e e 是轨道偏心率;对于椭圆 0 < e < 1 0
著名的哈雷彗星是一个椭圆,台湾的鹿林彗星是一个抛物线。
天文学家利用太空望远镜,观测到一个新的天体,上图的 原点 O O O 代表地球,坐标是极坐标系。
新天体,第一次观测出现的位置( 得到极坐标 ( Θ , r ) (\Theta,~r) (Θ, r):):
也就是,估计轨道常数参数 β \beta β、轨道偏心率 e e e。
因为我们已经得到了五组 ( Θ , r ) (\Theta,~r) (Θ, r),而天体的位置又必然满足轨道方程 r = β + e ( r c o s ( Θ ) ) r = \beta + e(r~cos(\Theta)) r=β+e(r cos(Θ)),就形成了五组二元一次方程。
- { 1 ⋅ β + 3.00 c o s ( 0.88 ) ⋅ e = 3.00 1 ⋅ β + 2.30 c o s ( 1.10 ) ⋅ e = 2.30 1 ⋅ β + 1.65 c o s ( 1.42 ) ⋅ e = 1.65 1 ⋅ β + 1.77 c o s ( 1.25 ) ⋅ e = 1.25 1 ⋅ β + 2.14 c o s ( 1.01 ) ⋅ e = 1.01 \left\{\begin{matrix} 1· \beta + 3.00~cos(0.88) ·e = 3.00 \\ 1· \beta + 2.30~cos(1.10) ·e = 2.30 \\ 1· \beta + 1.65~cos(1.42) ·e = 1.65 \\ 1· \beta + 1.77~cos(1.25) ·e = 1.25 \\ 1· \beta + 2.14~cos(1.01) ·e = 1.01 \end{matrix}\right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧1⋅β+3.00 cos(0.88)⋅e=3.001⋅β+2.30 cos(1.10)⋅e=2.301⋅β+1.65 cos(1.42)⋅e=1.651⋅β+1.77 cos(1.25)⋅e=1.251⋅β+2.14 cos(1.01)⋅e=1.01
看这些方程的类型,就是超定方程组 — 系数还有小数,基本消不了。
用矩阵表示(矩阵乘法):
- [ 1 3.00 c o s ( 0.88 ) 1 2.30 c o s ( 1.10 ) 1 1.65 c o s ( 1.42 ) 1 1.77 c o s ( 1.25 ) 1 2.14 c o s ( 1.01 ) ] ∗ [ β e ] = [ 3.00 2.30 1.65 1.25 1.01 ] \left[ \begin{matrix} 1 & 3.00~cos(0.88)\\ 1 & 2.30~cos(1.10)\\ 1 & 1.65~cos(1.42)\\ 1 & 1.77~cos(1.25)\\ 1 & 2.14~cos(1.01) \end{matrix} \right]* \left[ \begin{matrix} \beta\\ e \end{matrix} \right]= \left[ \begin{matrix} 3.00\\ 2.30\\ 1.65\\ 1.25\\ 1.01 \end{matrix} \right] ⎣⎢⎢⎢⎢⎡111113.00 cos(0.88)2.30 cos(1.10)1.65 cos(1.42)1.77 cos(1.25)2.14 cos(1.01)⎦⎥⎥⎥⎥⎤∗[βe]=⎣⎢⎢⎢⎢⎡3.002.301.651.251.01⎦⎥⎥⎥⎥⎤
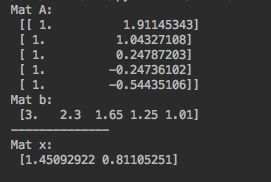
解得: β = 1.45 , e = 0.81 \beta = 1.45, ~e = 0.81 β=1.45, e=0.81。
所以,天体轨道方程为: r = 1.45 + 0.81 r c o s ( Θ ) r = 1.45+0.81r~cos(\Theta) r=1.45+0.81r cos(Θ)。
整理得: r = 1.45 1 − 0.81 c o s ( Θ ) r=\frac{1.45}{1-0.81~cos(\Theta)} r=1−0.81 cos(Θ)1.45
观测的数据越多,参数估计就越准确。
# 运行:在命令行输入 python 当前源文件.py
import numpy as np
import matplotlib.pyplot as plt
# 1.准备好观测到的 (θ,r) 数据 r = 贝塔 + e(r cosθ)
data = np.array([ [ 0.88, 3.00],
[ 1.10, 2.30],
[ 1.42, 1.65],
[ 1.77, 1.25],
[ 2.14, 1.01] ])
# 2.构建系数矩阵A
A = np.ones((data.shape[0],data.shape[1]))
for i in range(0,data.shape[0]): # i从 [0,5) 区间逐一取值
theta , r = data[i][0] , data[i][1]
A[i][1] = r * np.cos(theta)
print("Mat A:\n", A)
# 3.构造常数项矩阵b
b = data[:,1]
print("Mat b:\n", b)
# 4. 根据估值公式求解参数
x = np.dot(np.dot(np.linalg.inv(np.dot(A.T,A)), A.T),b)
print("--------------\nMat x:\n",x)
# 5. 画出天体运行轨道
theta_ = np.linspace(0, 2*np.pi, 100)
r_ = x[0] / (1-x[1]* np.cos(theta_))
graph = plt.subplot(111, polar=True) # 1行1列图像中的第一个
data_= data.T
graph.plot(data_[0,:],data_[1,:],'go') # 将已测量数据打上绿色的o('go')
graph.plot(theta_, r_ ,'r', linewidth=1)
plt.show()