利用余弦距离比较文档间的相似度
一.数据说明
在进行正式的操作之前,我想对后续进行处理的数据进行说明,首先,我在新浪网上爬取了中文体育新闻网页若干并提取了对应页面中的新闻内容,然后进行了中文分词(jieba)和删除停用词操作,最后处理的结果展示如下如所示:
注意:后续的操作都是在经过上述步骤处理的文档基础上!!!
二.根据文档建立词频矩阵
2.1 什么是词频?
词频(Term Frequency,tf)指某个词(term)在文章中出现次数,若某个词(不包括停用词)在文章中出现的频率很高,则说明这个词可能比较重要。
2.2 sklearn中的CountVectorizer类
对于词频矩阵的建立,这里直接调用sklearn库中的CountVectorizer类,通过该类的方法fit_transform()可以获取一个词频矩阵,其中每一行代表一个文档,每一列代表词在该文档中出现的频率,词频矩阵的结构如下图所示:
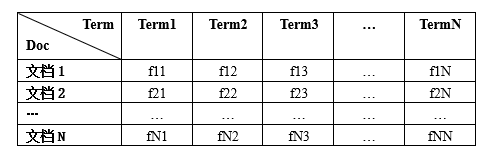
fit_transform()函数使用起来比较简便,只需传递一个"文档列表"即可,该列表中的每个元素为一个经处理后的文档字符串,例如:
doclists = [
'翟晓川 北京 男篮 放假 结束 此前 共 训练 天 新浪 竞技 风暴 竞技风暴 新浪 新浪网 北京 时间 月 日 北京 男篮 球员 翟晓川开 直播 球迷 聊 聊 疫情 期间 生活 球队 接下 下来 接下来 安排 翟晓川 透露 球队 此前 集中 训练 天 随后 放 一周 假 明天 北京 男篮 正式 恢复 训练 一个 一个月 大概 训练 天 翟晓川 北京 男篮 出场 时间 最多 球员 直播 中 展示 劳动 模范 劳动模范 徽章 证书 迈克 克尔 迈克尔',
...
'多名 高管 预计 公牛 解雇 主帅 新帅 候选 锁定 人 新浪 竞技 风暴 竞技风暴 新浪 新浪网 数名 不愿 透露 姓名 竞争 对手 竞争对手 高管 预计 公牛 解雇 主帅 博 伊伦 猛龙 助教 阿德 德里 里安 阿德里 阿德里安 格里 格里芬 人 助教 尤杜卡 新帅 候选',
...
]
该函数的使用示例代码如下:
vc = CountVectorizer() #构造一个CountVectorizer类对象
wfm = vc.fit_transform(doclists) #获取对应的词频矩阵
三.根据词频矩阵求tf-idf矩阵
3.1 tf-idf简介
tf上述步骤已经介绍,这里主要介绍一下idf。idf的全称为inverse document frequency,即反向文档频率,它的含义是包含某个词的文档数,其计算公式为: i d f = log 10 ( N / d f t ) idf=\log_{10}(N/df_t) idf=log10(N/dft)
其中 N N N为文档总数, d f t df_t dft为所有文档中包含词汇t的文档数,从该公式可知,一个词越常见, i d f idf idf越低。tf-idf就是将二者乘起来,即 t f i d f = t f × i d f tfidf=tf\times{idf} tfidf=tf×idf。
3.2 sklearn中的TfidfTransformer类
要想求得包含文档中对应词的tf-idf值的tf-idf矩阵,可以使TfidfTransformer类,通过该类的fit_transform()方法可以获取对应的tf-idf矩阵,其结构如下图所示:
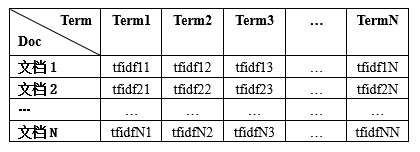
该类的fit_transform()函数只需要传入之前通过CountVectorizer类得到的矩阵即可得到一个词频矩阵,其示例代码如下:
transformer = TfidfTransformer() #构造一个TfidfTransformer实例
tmatrix = transformer.fit_transform(wfm) #获取tf-idf矩阵
四.L2归一化
4.1 计算公式
设一个向量 ( x 1 , x 2 , x 3 , . . . , x N ) (x_1,x_2,x_3,...,x_N) (x1,x2,x3,...,xN),其归一化后的向量为 ( y 1 , y 2 , y 3 , . . . , y N ) (y_1,y_2,y_3,...,y_N) (y1,y2,y3,...,yN),则归一化的公式为:
y i = x i ∑ 1 N x i 2 y_i={x_i\over{\sqrt{\sum_1^N{x_i^2}}}} yi=∑1Nxi2xi
4.2 示例代码
def L2Normalization(matrix):
"""
matrix:文档的tfidf矩阵,每一行为一个文档各个term的tfidf值
输出为进行L2正则化后的矩阵
"""
return matrix / np.sqrt(np.sum(matrix ** 2,axis=1,keepdims=True))
需要注意的是在调用该函数之前,需要将上述求得的tfidf矩阵,转换为numpy的ndarray对象,具体做法为:
matrix = np.array(tmatrix)
五.求余弦距离
5.1计算公式
由于上述的tfidf矩阵进行了L2归一化,因此求两个文档的余弦距离的公式为: c o s ( q ⃗ , d ⃗ ) = q ⃗ ⋅ d ⃗ = ∑ i = 1 N q i d i cos(\vec{q},\vec{d})=\vec{q}\cdot\vec{d}=\sum_{i=1}^N{q_id_i} cos(q,d)=q⋅d=i=1∑Nqidi
经过计算后的余弦距离矩阵结构如下:
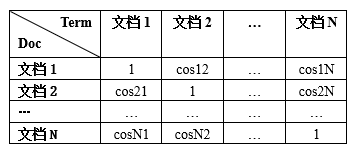
在该余弦距离矩阵中 a r r [ i ] [ j ] = c o s i j arr[i][j] = cosij arr[i][j]=cosij的含义是,文档 i i i和文档 j j j之间的余弦距离为 c o s i j cosij cosij,可知该余弦距离矩阵是一个对称方阵,即 a r r [ i ] [ j ] = a r r [ j ] [ i ] arr[i][j]=arr[j][i] arr[i][j]=arr[j][i]。
5.2 示例代码
def cosineDistance(nmatrix):
"""
nmatrix:L2正则化后的tfidf矩阵
输出包含各个文档的余弦距离矩阵,例如
1 2 3
1 c1 c2 c3
2 c2 c4 c5
3 c3 c5 c6
m[0,1]表示文档1和文档2之间的余弦距离
"""
return np.matmul(nmatrix,nmatrix.T)
六.结果展示
在求得对应的文档间余弦距离矩阵后利用np.where()函数筛选出文档余弦距离大于0.9的文档对,示例代码为:
x,y = np.where(arr > 0.9) #arr为余弦距离矩阵
for i,j in zip(x,y):
if i != j:
print("Doc {} Doc{} CosineDistance {}".format(i,j,arr[i][j]))
部分输出结果为:
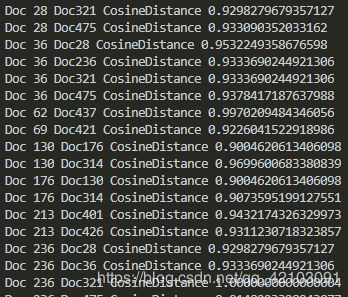
这里我随机挑选两个余弦距离大于0.9的文档进行展示:

从上述展示结果也可以看出,两篇新闻极其的相似。以上便是本文的全部内容,要是觉得不错支持一下吧!!!