网络流——最大流

一、什么是网络流

网络流是指给定一个有向图，其中有两个特殊的点：源点 $s$（Source）和汇点 $t$（Sink）；每条边都有一个指定的流量上限，下文均称之为容量（Capacity），即经过这条边的流量不能超过容量，这样的图被称为网络流图。同时，除了源点和汇点外，所有点的入流和出流都相等，源点只有流出的流，汇点只有流入的流，网络流就是从 $s$ 到 $t$ 的一个可行流。

二、可行流、最大流

定义 $c(u,v)$ 表示边 $(u,v)$ 的容量，$f(u,v)$ 表示边 $(u,v)$ 的流量。如果满足 $0\le f(u,v)\le c(u,v)$，则称$f(u,v)$ 为边 $(u,v)$ 上的流量。

如果有一组流量满足：源点 $s$ 的流出量等于整个网络的流量，汇点 $t$ 的流入量等于整个网络的流量，除了任意一个不是 $s$ 或 $t$ 的点的总流入量等于总流出量。那么整个网络中的流量被称为一个可行流。

在所有可行流中，最大流指其中流量最大的一个流的流量。

三、相关定义

1. 源点 $s$：只有流出量的点。
2. 汇点 $t$：只有流入量的点。
3. 容量 $c$：$c(u,v)$ 表示边 $(u,v)$ 上的容量。
4. 流量 $f$：$f(u,v)$ 表示边 $(u,v)$ 上的流量。
5. 残量 $w$：$w(u,v)$ 表示边 $(u,v)$ 上的残量（显然有 $w(u,v)=c(u,v)-f(u,v)$）。

四、网络流的性质

1.容量限制
对于任何一条边，都有 $0\le f(u,v)\le c(u,v)$。

2.斜对称性
对于任何一条边，都有 $f(u,v)=-f(v,u)$。即从 $u$ 到 $v$ 的流量一定等于从 $v$ 到 $u$ 的流量的相反数。

3.流守恒性
对于任何一个点 $u$，如果满足 $u\ne s$ 并且 $u\ne t$，那么一定有 $\sum f(u,v)=0$，即 $u$ 到相邻节点的流量之和为 $0$。因为 $u$ 本身不会制造和消耗流量。

五、最大流的求解

增广路思想

1. 找到一条从 $s$ 到 $t$ 的路径，使得路径上的每一条边都有 $w(u,v)>0$ 即残量大于 $0$。注意：这里是严格 $>$ 而不是$\ge$，这意味着这条边还可以分配流量。这条路径就被叫做増广路。
2. 找到这条路径上最小的 $w(u,v)$，记为 $flow$。将这条路径上的每一条边的$w(u,v)$ 减去 $flow$。
3. 重复上述过程，直到找不到増广路为止。

不防依照这个思想先模拟一遍：

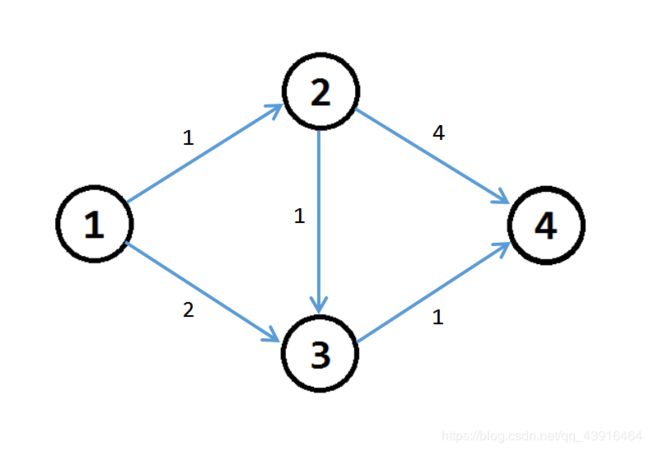
如果我们把每条边的的信息用残量 / 容量表示出来，可以得到下图：

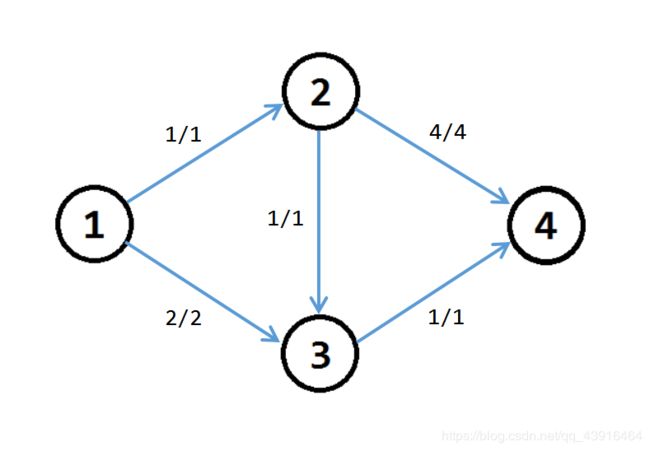
假设我们第一次找到的増广路为$1-2-3-4$，那么我们把这条路径上的边的 $w(u,v)$ 减去 $minf(u,v)$ 即 $1$，得到下图：

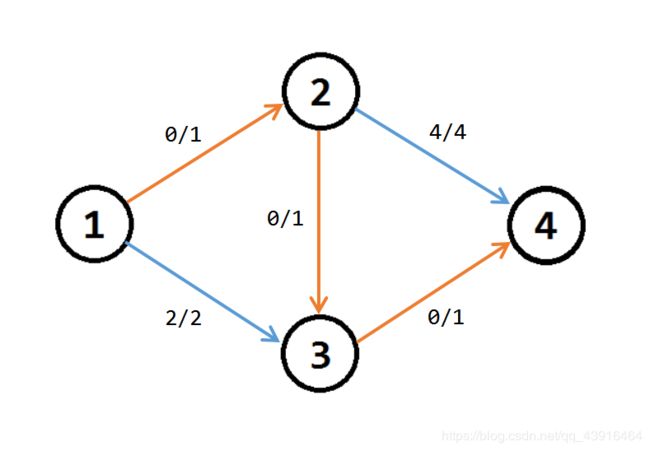
然后我们发现已经没有増广路了，此时算出来的“最大流”为 1。但是我们可以手动计算一下，这张图的最大流其实是 2。这个最大流的路径为 $1-2-4$（流量为 $1$）和 $1-3-4$（流量为 $1$）。

因此，我们可以发现这样的过程是错误的。原因就是増广路在一定意义上是有顺序的，说白了就是没有给它反悔的机会。所以接下来我们要引入反向边的概念。

反向边思想
通过上文的分析我们已经知道，当我们在寻找増广路的时候，找到的并不一定是最优解。如果我们对正向边的 $w(u,v)$ 减去 $flow$ 的同时，将对应的反向边的 $w(v,u)$ 加上 $flow$，我们就相当于可以反悔从这条边流过。

那么我们可以建立反向边，初始时每条边的 $w(u,v)=c(u,v)$，它的反向边的 $w(v,u)=0$（显然反向边不能有流量，因此残量为 $0$）。

接下来再看一下上面那个例子，我们只用 $w(u,v)$ 来表示每条边（包括反向边）的信息：

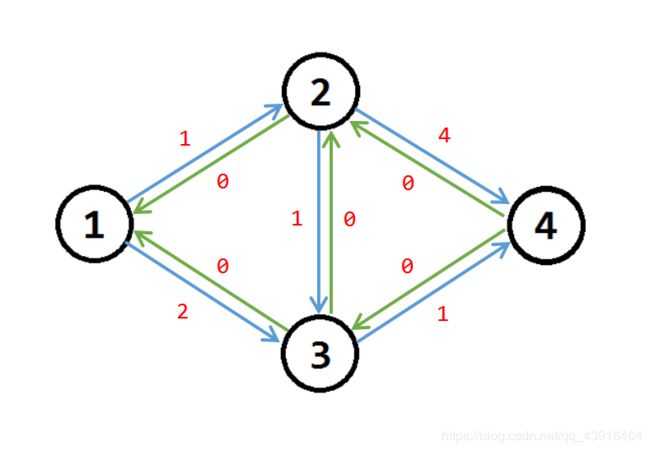
接下来开始寻找増广路，假如还是 $1-2-3-4$ 这条路径。

我们需要把 $w(1,2)$，$w(2,3)$，$w(3,4)$ 减少 $1$，同时把反向边的 $w(2,1)$，$w(3,2)$，$w(4,3)$ 增加 1。那么可以得到下图：

继续从 $s$ 开始寻找増广路（不需要考虑边的类型），显然可以发现路径 $1-3-2-4$，其中 $flow=1$。更新边的信息，得到下图：

此时我们发现没有増广路了，为了直观观察这个网络，我们去掉反向边，显然我们求出的最大流为 2

正确性
当我们第二次増广边 $(2,3)$ 走这条反向边 $(3,2)$ 时，把 $(2,3)$ 和 $(3,2)$ 的流量抵消了，相当于把 $(2,3)$ 这条正向边的流量给退了回去使得可以不走 $(2,3)$ 这条边。

如果反向边 $(v,u)$ 的流量不能完全抵消正向边 $(u,v)$，那么意味着从 $u$ 开始还可以流一部分流量到 $v$，这样也是允许的。

思路总结

1. 最初这个网络的流量为 0，称为零流。
2. 找到一条从 $s$ 到 $t$ 的路径，使得路径上的每一条边都有 $w(u,v)>0$ 即残量大于 $0$。注意：这里是严格 $>$ 而不是$\ge$，这意味着这条边还可以分配流量。这条路径就被叫做増广路。
3. 找到这条路径上最小的 $w(u,v)$，记为 $flow$。
4. 将这条路径上的每一条边的 $w(u,v)$ 减去 $flow$，同时将反向边 $(v,u)$ 的 $w(v,u)$ 加上 $flow$。
5. 重复上述过程，直到找不到増广路为止，此时的流量就是最大流。

六、算法实现

最大流算法主要有两类，增广路算法和预留推进算法，下面介绍的两种算法都属于增广路算法。
增广路算法都是基于增广路定理（Augmenting Path Theorem）：网络达到最大流当且仅当残留网络中没有増广路。

• Ford-Fulkerson（FF算法）
  思路：增广路思想的完全模拟，它通过深度优先搜索来寻找增广路，并沿着它增广，直到找不到增广路为止。
  老规矩，上代码之前先来道模板题：【模板】网络最大流
  c++代码：

#include 
using namespace std;
const int maxn=1e5+7,inf=0x3f3f3f3f;
int n,m,s,t;
bool used[maxn];  //DFS中用到的访问标记
struct node{  //用于表示边的结构体（终点、容量、反向边）
    int to,cap,rev;
};
vector<node> v[maxn];  //图的邻接表表示
void add(int from,int to,int cap){  //向图中增加一条从from到to容量为cap的边
    v[from].push_back((node){to,cap,v[to].size()});
    v[to].push_back((node){from,0,v[from].size()-1});
}
int dfs(int x,int t,int f){  //通过DFS寻找增广路
    if(x==t) return f;
    used[x]=true;
    for(int i=0;i<v[x].size();i++){
        node &e=v[x][i];
        if(!used[e.to]&&e.cap>0){
            int d=dfs(e.to,t,min(f,e.cap));
            if(d>0){
                e.cap-=d;
                v[e.to][e.rev].cap+=d;
                return d;
            }
        }
    }
    return 0;
}
int Ford_Fulkerson(int s,int t){  //求解从s到t的最大流
    int flow=0;
    while (1)
    {
        memset(used,false,sizeof(used));
        int f=dfs(s,t,inf);
        if(!f) return flow;
        flow+=f;
    }
    
}

int main(){
    cin>>n>>m>>s>>t;
    while(m--){
        int x,y,z;
        cin>>x>>y>>z;
        add(x,y,z);
    }
    cout<<Ford_Fulkerson(s,t);
    return 0;
}

时间复杂度：记最大流的流量为$F$，那么$Fork-fulkerson$算法最多进行$F$次深度优先搜索，所以其复杂度为$O(F|E|)$。不过，这是一个很松的上界，达到这种最坏复杂度的情况几乎不存在。所以在多数情况下，即便通过估算得到的复杂度偏高，实际运用当中也还是比较快的。

• Dinic
  思路：与$FF$算法相对，$Dinic$算法总是寻找最短的增广路，并沿着它增广。因为最短增广路的长度在增广过程中始终不会变短，所以无需每次都通过深度预先搜索来寻找最短增广路，我们可以先进行一次宽度优先搜索，然后考虑由近距离顶点指向远距离顶点的边所组成的分层图，在上面进行深度优先搜索寻找最短增广路。如果在分层图上找不到新的增广路了，则说明最短增广路的长度确实变长了，或不存在增广路了，于是重新通过宽度优先搜索构造新的分层图。此外，还可以对这个算法进行优化。
  当前弧优化：在每次对分层图进行深度优先搜索寻找增广路时，避免对一条没有用的边进行多次检查。
  c++代码：

#include 
using namespace std;
const int maxn=1e5+7,inf=0x3f3f3f3f;
int n,m,s,t,level[maxn],iter[maxn]; //level：顶点到源点的距离标号 iter：当前弧，在其之前的边已经没有用了
struct node{
    int to,cap,rev;
};
vector<node> v[maxn];
void add(int from,int to,int cap){
    v[from].push_back((node){to,cap,v[to].size()});
    v[to].push_back((node){from,0,v[from].size()-1});
}
int bfs(int s){  //通过BFS计算从源点出发的距离标号
    memset(level,0,sizeof(level));
    queue<int> q;
    level[s]=1;
    q.push(s);
    while(!q.empty()){
        int x=q.front();
        q.pop();
        for(int i=0;i<v[x].size();i++){
            node e=v[x][i];
            if(e.cap&&!level[e.to]){
                level[e.to]=level[x]+1;
                q.push(e.to);
            }
        }
    }
    return level[t];
}
int dfs(int x,int t,int f){  //通过DFS寻找增广路
    if(x==t) return f;
    for(int &i=iter[x];i<v[x].size();i++){
        node &e=v[x][i];
        if(e.cap&&level[x]<level[e.to]){
            int d=dfs(e.to,t,min(f,e.cap));
            if(d){
                e.cap-=d;
                v[e.to][e.rev].cap+=d;
                return d;
            }
        }
    }
    return 0;
}
int Dinic(int s,int t){  //求解从s到t的最大流
    int flow=0;
    while(bfs(s)){
        memset(iter,0,sizeof(iter));
        int f;
        while((f=dfs(s,t,inf))){
            flow+=f;
        }
    }
    return flow;
}
int main(){
    cin>>n>>m>>s>>t;
    while(m--){
        int x,y,z;
        cin>>x>>y>>z;
        add(x,y,z);
    }
    cout<<Dinic(s,t);
    return 0;
}

时间复杂度：每一步构造分层图的复杂度为$O(|E|)$，加入当前弧优化后，可以保证对每次分层图进行深度优先搜索复杂度为$O(|E||V|)$，而每一步完成之后最短增广路的长度都会至少增加1，由于增广路的长度不会超过$|V|-1$，因此最多重复O(|V|)步就可以了，这样总的复杂度就是$O(|E||V|$²)。不过，该算法在实际应用中速度非常快，很多时候即便图的规模比较大也没有问题。

• 两种算法的对比
  评测记录：
  
  第一个是Dinic算法，耗时470ms，第二个是FF算法，耗时1220ms。

总结：99%的网络流算法，都可以用Dinic去解。卡Dinic的毒瘤出题人，都是*哔*

不好意思爆粗口了，不过，还真的有这种毒瘤出题人，
【模板】最大流 加强版 / 预流推进
解决这道题就必须要用我上面说的第二种最大流算法：预流推进法。
但是我太懒（蒻）了，现在并不想去写那种算法，就交给你们了QWQ

七.最大流的应用

洛谷P1345奶牛的电信
做这道题之前，先说一个很重要的定理：
最大流最小割定理：最大流等于最小割。
那么，最小割又是什么呢？最小割是要求为了使原点（记为S）和汇点（记为T）不连通，最少要割几条边。
好了，你是不是觉得你可以去做这道题了（其实说的就是我 ），裸的割边，打个Dinic就行了，但有时候我们还是太naive了。
重新读题，会发现这题割的不是边，是点。所以说，我们需要一个割边转割点的小技巧。
我们可以考虑“拆点”，即把一个点拆成两个点，中间连一条边权为1的边。
前一个点作为“入点”，别的点连边连入这里。
后一个点作为“出点”，出去的边从这里出去。
这样，只要我们切断中间那条边，就可以等效于除去这个点，如图：

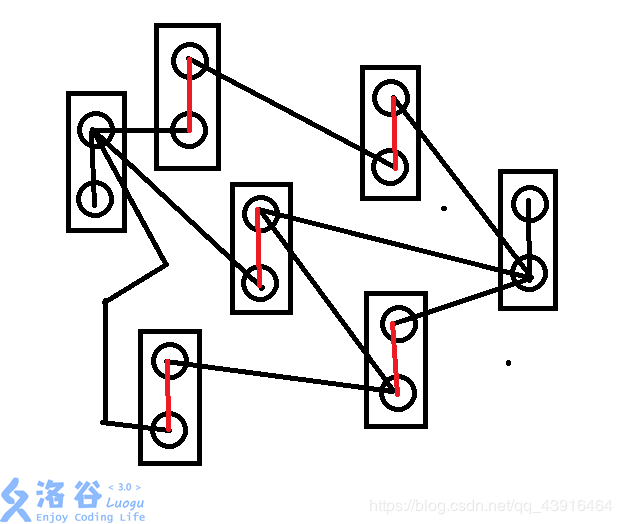
红色的边边权为1，黑色的边边权为$inf$。

原点和汇点的内部边权为$inf$，因为显然这两个点不能删除。

题面给的边删除没意义（因为我们要删点），所以也设为inf(事实上设为1也没问题，因为删除这条边的权值可以理解为删除了一个点)

至此，我们就可以把这道题AC了
c++代码：

#include 
using namespace std;
const int maxn=1e5+7,inf=0x3f3f3f3f;
int n,m,s,t,level[maxn],iter[maxn];
struct node{
    int to,cap,rev;
};
vector<node> v[maxn];
void add(int from,int to,int cap){
    v[from].push_back((node){to,cap,v[to].size()});
    v[to].push_back((node){from,0,v[from].size()-1});
}
int bfs(int s){
    memset(level,0,sizeof(level));
    queue<int> q;
    level[s]=1;
    q.push(s);
    while(!q.empty()){
        int x=q.front();
        q.pop();
        for(int i=0;i<v[x].size();i++){
            node e=v[x][i];
            if(e.cap&&!level[e.to]){
                level[e.to]=level[x]+1;
                q.push(e.to);
            }
        }
    }
    return level[t];
}
int dfs(int x,int t,int f){
    if(x==t) return f;
    for(int &i=iter[x];i<v[x].size();i++){
        node &e=v[x][i];
        if(e.cap&&level[x]<level[e.to]){
            int d=dfs(e.to,t,min(f,e.cap));
            if(d){
                e.cap-=d;
                v[e.to][e.rev].cap+=d;
                return d;
            }
        }
    }
    return 0;
}
int Dinic(int s,int t){
    int flow=0;
    while(bfs(s)){
        memset(iter,0,sizeof(iter));
        int f;
        while((f=dfs(s,t,inf))){
            flow+=f;
        }
    }
    return flow;
}
int main(){
    cin>>n>>m>>s>>t;
    for(int i=1;i<=n;i++){
        if(i==s||i==t){
            add(i,i+n,inf);
        }
        else add(i,i+n,1);
    }
    while(m--){
        int x,y;
        cin>>x>>y;
        add(x+n,y,inf);
        add(y+n,x,inf);
    }
    cout<<Dinic(s,t);
    return 0;
}