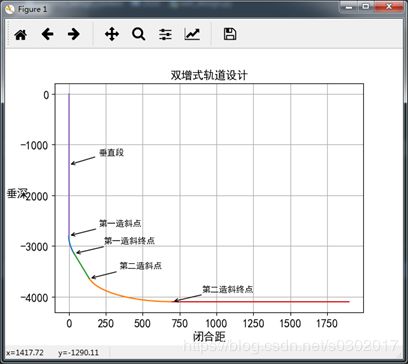
python双增式轨道设计

import pandas as pd
import numpy as np
from numpy import sin
from numpy import cos
from numpy import tan
from numpy import arctan
from numpy import arccos
import matplotlib.pyplot as plt
from pylab import mpl
from mpl_toolkits.mplot3d import Axes3D
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
#参数
D_t=4100#目标段井深
C_t=700#目标段闭合距
D_k=2800#造斜点井深
C_k=0#造斜点闭合距
alpha_k=0#造斜点斜率
K_z=1#第一造斜率
K_zz=3#第二造斜率
alpha_t=np.pi/2#目标段井斜角
Delta_Ltd=1200#目标段长度（水平段长度）

#定向井双增式轨道设计,单位均为弧度
def two_buildup(D_t,C_t,D_k,C_k,alpha_k,K_z,alpha_t,Delta_Ltd,K_zz):
    #曲率
    R_z=1719/K_z#求曲率半径
    R_zz=1719/K_zz#求曲率半径

    #关键参数
    D_e=D_t-D_k+R_z*sin(alpha_k)-R_zz*sin(alpha_t)#双增式轨道
    C_e=C_t-C_k-R_z*cos(alpha_k)+R_zz*cos(alpha_t)#双增式轨道
    R_e=R_z-R_zz#双增式轨道
    Delta_Lbc=np.sqrt(D_e**2+C_e**2-R_e**2)
    alpha_b=2*arctan((D_e-Delta_Lbc)/(R_e-C_e))
    print('稳斜段长度:',Delta_Lbc)
    print('稳斜段井斜角:',np.degrees(alpha_b))
    #造斜点井深
    L_k=D_k/cos(alpha_k)

    #增斜终点b
    L_b=L_k+R_z*(alpha_b-alpha_k)
    D_b=D_k+R_z*(sin(alpha_b)-sin(alpha_k))
    C_b=C_k+R_z*(cos(alpha_k)-cos(alpha_b))

    #稳斜终点c
    L_c=L_b+Delta_Lbc
    D_c=D_b+Delta_Lbc*cos(alpha_b)
    C_c=C_b+Delta_Lbc*sin(alpha_b)

    #双增第二增斜终点t
    L_t=L_c+R_zz*(alpha_t-alpha_b)
    D_t=D_c+R_zz*(sin(alpha_t)-sin(alpha_b))
    C_t=C_c+R_zz*(cos(alpha_b)-cos(alpha_t))

    #双增第二稳斜终点d
    L_d=L_t+Delta_Ltd
    D_d=D_t+Delta_Ltd*cos(alpha_t)
    C_d=C_t+Delta_Ltd*sin(alpha_t)
    LDC=np.array([[L_k,D_k,C_k],[L_b,D_b,C_b],[L_c,D_c,C_c],[L_t,D_t,C_t],[L_d,D_d,C_d]])
    return LDC

#最小曲率求两点之间圆弧，角度为弧度
def minimum_curvature_method(X,Y,Z,L,phi,alpha):
    DNE = pd.DataFrame(columns=list('DNE'))
    DNE.loc[0, 'D']=Z
    DNE.loc[0, 'N']=Y
    DNE.loc[0, 'E']=X
    for i in range(len(L)-1):
        Delta_L=L[i+1]-L[i]
        Delta_phi=phi[i+1]-phi[i]
        gamma = arccos(cos(alpha[i])*cos(alpha[i+1]) + sin(alpha[i])*sin(alpha[i+1])*cos(Delta_phi))
        lambda_M = Delta_L*tan(gamma/2)/gamma
        Delta_D=lambda_M*(cos(alpha[i])+cos(alpha[i+1]))
        Delta_N=lambda_M*(sin(alpha[i])*cos(phi[i]) +sin(alpha[i+1])*cos(phi[i+1]))
        Delta_E=lambda_M*(sin(alpha[i])*sin(phi[i]) +sin(alpha[i+1])*sin(phi[i+1]))
        DNE.loc[i+1,'D']=Delta_D+DNE.loc[i,'D']
        DNE.loc[i+1,'N']=Delta_N+DNE.loc[i,'N']
        DNE.loc[i+1,'E']=Delta_E+DNE.loc[i,'E']
    return DNE

LDC=two_buildup(D_t,C_t,D_k,C_k,alpha_k,K_z,alpha_t,Delta_Ltd,K_zz)#求各个节点的长度，位置

#绘制造斜圆弧段
R_z=1719/K_z#求曲率半径
R_zz=1719/K_zz#求曲率半径
theta1=(LDC[1,0]-LDC[0,0])/R_z#第一段的井斜角
L=np.linspace(LDC[0,0],LDC[1,0],100)
phi=np.zeros(100)#造斜方位角
alpha=np.linspace(0,theta1,100)
DNE=minimum_curvature_method(X=0,Y=0,Z=D_k,L=L,phi=phi,alpha=alpha)
plt.plot(DNE['N'],-DNE['D'])#绘制第一造斜段
#绘制第二段
theta2=(LDC[3,0]-LDC[2,0])/R_zz#第二段的井斜角
L=np.linspace(LDC[2,0],LDC[3,0],100)
phi=np.zeros(100)#造斜方位角
alpha=np.linspace(theta1,theta1+theta2,100)
DNE=minimum_curvature_method(X=0,Y=LDC[2,2],Z=LDC[2,1],L=L,phi=phi,alpha=alpha)
plt.plot(DNE['N'],-DNE['D'])#绘制第二造斜段
print(LDC)
print(DNE)
plt.plot(LDC[1:3,2],-LDC[1:3,1])#绘制稳斜段
plt.plot(LDC[3:5,2],-LDC[3:5,1])#绘制水平段
plt.plot([0,0],[-0,-D_k])#绘制垂直段

plt.annotate('垂直段',xy=(0,-LDC[0,1]/2),xytext=(0+200,-LDC[0,1]/2+200),arrowprops=dict(arrowstyle='->',connectionstyle='arc3'))
plt.annotate('第一造斜点',xy=(LDC[0,2],-LDC[0,1]),xytext=(LDC[0,2]+200,-LDC[0,1]+200),arrowprops=dict(arrowstyle='->',connectionstyle='arc3'))
plt.annotate('第一造斜终点',xy=(LDC[1,2],-LDC[1,1]),xytext=(LDC[1,2]+200,-LDC[1,1]+200),arrowprops=dict(arrowstyle='->',connectionstyle='arc3'))
plt.annotate('第二造斜点',xy=(LDC[2,2],-LDC[2,1]),xytext=(LDC[2,2]+200,-LDC[2,1]+200),arrowprops=dict(arrowstyle='->',connectionstyle='arc3'))
plt.annotate('第二造斜终点',xy=(LDC[3,2],-LDC[3,1]),xytext=(LDC[3,2]+200,-LDC[3,1]+200),arrowprops=dict(arrowstyle='->',connectionstyle='arc3'))

# plt.annotate('第一降斜段，降斜率1°/30m',xy=(LDC[0,2]+20,-LDC[0,1]-300),xytext=(LDC[0,2]+100,-LDC[0,1]),arrowprops=dict(arrowstyle='->',connectionstyle='arc3'))
# plt.annotate('稳斜段长度：503.56m\n井斜角：11.78°',xy=(LDC[1,2]+60,-LDC[1,1]-300),xytext=(LDC[1,2]+200,-LDC[1,1]),arrowprops=dict(arrowstyle='->',connectionstyle='arc3'))
# plt.annotate('第二降斜段，降斜率3°/30m',xy=(LDC[2,2]+200,-LDC[2,1]-280),xytext=(LDC[2,2]+300,-LDC[2,1]+200),arrowprops=dict(arrowstyle='->',connectionstyle='arc3'))

plt.xticks(fontsize=13)
plt.xlabel(u'闭合距',fontsize=13)
plt.yticks(fontsize=13)
plt.ylabel(u'垂深',fontsize=13,rotation=0)
plt.title(u'双增式轨道设计',fontsize=13)
plt.grid(True)
plt.show()
DNE.to_excel(r'C:\Users\Administrator\Desktop\upupup\2-petrol_design_contest\2020\result.xls')
print('下载完毕，保存至result.xls')

 作者：ChenBD