python 中的数组转置和轴对称，T/transpose/swapaxes

最近在学python的数据分析，于是发现了一本好书《利用python进行数据分析》。说实话前两章不知道作者在说什么（无奈），然后我就直接跳到了第四章（numpy基础：数组和矢量计算），好了，不啰嗦了，正文开始。

声明：作者用的是python2.7

转置是重塑的一种特殊形式，他返回的是源数据的视图（不会进行任何复制操作，这一点要和花式索引不太一样，后者总是将数据复制到新数组中）。
完成转置可以通过三种方式：

1. transpose方法；
2. T属性；
3. swapaxes方法。

首先要说最简单的T属性，话不多说先放代码

In [1]: arr = np.arange(15).reshape((3,5))
In [2]: arr
out [2]:
array([[0,1,2,3,4],
       [5,6,7,8,9],
       [10,11,12,13,14]])
In [3]:arr.T
out [3]:
array([[0,5,10],
       [1,6,11],
       [2,7,12],
       [3,8,13],
       [4,9,14]])

虽然上述内容写在代码块中，但实际上是我按照书上内容手打的。但笔者还是要证明一下，我在本机上验证过，结果同IPython输出。
上述代码
In［1］表示将0－14按顺序填入一个三行五列的数组，
In［3］表示数组转置。
通过这个例子可以看出其实T属性适用于一，二维数组中。

那么在高维数组中，我们可以使用transpose方法。前方高能来了，书上给出的解释是：对于高维数组，transpose需要得到一个由轴编号组成的元祖才能对这些轴进行转置。
这句话我翻来覆去读了好几遍，然并卵。后来看了作者的例子才差不多明白。所谓的轴编号就是对维度进行编号。我们先看例子：

>>> import numpy as np
>>> arr = np.arange(16).reshape((2,2,4))
>>> arr
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7]],

       [[ 8,  9, 10, 11],
        [12, 13, 14, 15]]])
>>> arr.transpose((1,0,2))
array([[[ 0,  1,  2,  3],
        [ 8,  9, 10, 11]],

       [[ 4,  5,  6,  7],
        [12, 13, 14, 15]]])

  好吧，我还是换回我自己的编辑器了（>>>表示输入，无符号开头表示输出，笔者用的是VS code终端写的），不管了，继续解释。初始arr表示按顺序填入0－15的2＊2＊4矩阵，通过我之前所说，transpose的轴编号就是将维度编号,所以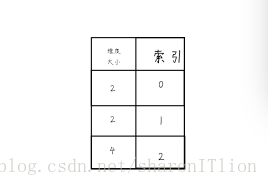![维度索引图](https://img-blog.csdn.net/20171103211302929?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvc2hhcm9uSVRsaW9u/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)
  而转置实际上就是第一维度和第二维度的转置，所以三维数组的维度索引由0，1，2变成了1，0，2 即后来代码中的transpose（（1，0，2））由来
  在补充一点

>>> arr.transpose()
array([[[ 0,  8],
        [ 4, 12]],

       [[ 1,  9],
        [ 5, 13]],

       [[ 2, 10],
        [ 6, 14]],

       [[ 3, 11],
        [ 7, 15]]])

如果transpose中未带任何参数则表示和T属性的效果相同, 其实是transpose（（2，1，0））完全转置，举个例子5原来的位置是［0，1，1］转置后变为［1，1，0］

>>> arr.transpose((2,1,0))[1,1,0]
5
>>> arr[0,1,1]
5

最后来说一下swapaxes 方法，它需要接受两个参数，其实就是他的轴编号。
如arr.swapaxes（1，2）表示第二三维度变换

>>> arr.swapaxes(1,2)
array([[[ 0,  4],
        [ 1,  5],
        [ 2,  6],
        [ 3,  7]],

       [[ 8, 12],
        [ 9, 13],
        [10, 14],
        [11, 15]]])

以6为例［0，1，2］转置后变为［0，2，1］

>>> arr.swapaxes(1,2)[0,2,1]
6
>>> arr[0,1,2]
6

说的不好，若有错请指出，谢谢