线性表(链式存储结构)
前言
线性表(顺序存储结构-用数组描述)
为了解决顺序存储不足:用线性表另外一种结构-链式存储。在顺序存储结构(数组描述)中,元素的地址是由数学公式决定的,而在链式储存结构中,元素的地址是随机分布的,每个元素都有一个明确的指针指向线性表的下一个元素的位置(即地址)。
1 链表描述
线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素,这组存储单元可以是连续的,也可以是不连续的。在顺序结构中,每个数据元素只需要存数据元素信息就行了,而在链式结构中,除了存储数据元素信息外,还要存储它的后继元素的存储地址。所以一般结点包括两个信息:数据和指针。链表就是n个节点组成的,如果每个结点只包含一个指针,那么就是单链表。
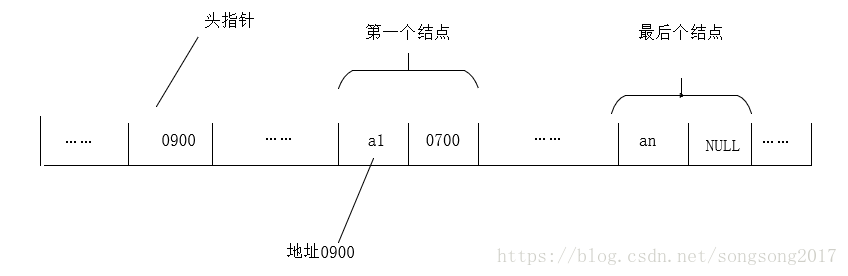
有头有尾:我们把链表中第一个结点的存储位置叫作头指针,那么整个链表的存取就必须是从头指针开始进行的。而线性链表的最后一个结点指针为空(NULL)。从图中可以看到,结点都是由两部分组成,数据域和指针域。
有时,为了更方便对链表进行操作,会在单链表的第一个结点前加一个头结点。头结点的数据域可以不存储任何信息,也可以存储如线性表长度等附加信息,头结点的指针域存储指向第一个结点的指针。
e
![]()
(ps:大话数据结构-P58页,图3-6-4,3-6-6有误,当初理解这里花了好长时间,图文表现的不是一个意思,无语!)
头指针和头结点的异同
头指针
(1)指链表指向第一个结点的指针,若链表有头结点,则是指向头结点的指针。
(2)头指针具有标识作用,所以常用头指针冠以链表的名字。
(3)无论链表是否为空,头指针均不为空。头指针是链表的必要元素。
(这句话真的歧义,若没有头结点,头指针head指向第一个节点,当空表时,head=NULL。应该是必须要有头指针。唉,这国内书看起来真的累)
头结点
(1)头结点是为了操作的统一和方便而设立的,放在第一个元素的结点之前,其数据域一般无意义(也可存放链表的长度)
(2)有了头结点,对在第一元素结点前插入结点和删除第一结点,其操作与其它结点的操作就统一了。
(3)头结点不一定是链表必须的要素。
2 链表实现
为了用链表描述线性表,要定义个一个结构体chainNode和一个类chain。
//链表节点的结构定义
template
struct chainNode
{
//数据成员
T element;
chainNode *next;
//方法
chainNode() {};
chainNode(const T& element) {this->element = element;}
chainNode(const T& element, chainNode* next) {
this->element = element;
this->next = next;
}
};
类chain用单向链表实现了线性表,其中最后一个结点的指针域为NULL,即它用单向链接的一组结点实现线性表。数据成员firstNode是指向首元素(即线性表第0个元素的结点)结点的指针。当链表为空时,firstNode的值为NULL。listSize表示线性表元素的个数,它等于链表节点的个数。
template
class chain : piblic linearList
{//linearList虚基类定义在本文头部-顺序存储结构一文里
public:
//构造函数,复制构造函数和析构函数
chain(int initialCapacity = 10);
chain (const chain&);
~chain();
//抽象数据类型ADT的方法
bool empty() const {return listSize == 0;}
int size() const {return listSize;}
T& get(int theIndex) const;
int indexOf(const T& theElement) const;
void erase(int theIndex);
void insert(int theIndex, const T& theElement);
protected:
void checkIndex(int theIndex) const;
//如果索引无效,抛出异常
chainNode* firstNode; //指向链表第一个节点的指针
int listSize; //线性表元素个数
};
为了创建一个空链表,只需要令指向第一个结点指针firstNode的值为NULL。与数组描述的线性表不同的是,链表在创建的时候不需要估计元素的最大个数以分配初始空间。不过,构造函数还是具有一个表示初始容量的形参initialCapacity,目的是与arrayList相容。(arrayList也在本文头链接文中)啥时候能体现这种相容性呢,如可能需要一个类型为linearList的数组,对数组成员的初始化将会用到如下所示的每一种形式的构造函数:
linearList
list[0] = new arrayList
list[1] = new arrayList
list[2] = new chain
list[3] = new chain
2.1 实现构造函数
template
chain::chain(int initialCapacity)
{//默认构造函数
if (initialCapacity < 1)
{
ostringstream s;
s << "Initial capacity = " << initialCapacity << "Must be > 0";
throw illegalParameterValue(s.str());
}
firstNode = NULL;
listSize = 0;
}
template
chain::chain(const chain& theList)
{复制构造函数
listSize = theList.listSize;
if (listSize == 0)
{//链表为空
firstNode = NULL;
return;
}
//链表theList为非空
chainNode* sourceNode = theList.firstNode;
//要复制链表theList的结点
firstNode = new chainNode(sourceNode->element);
//复制链表theList的首元素
sourceNode = sourceNode->next;
chainNode* targetNode = firstNode;
//当前链表*this的最后一个结点
while (sourceNode != NULL)
{//复制剩余元素
targetNode->next = new chainNode(sourceNode->element);
targetNode = target->next;
sourceNode = sourceNode->next;
}
targetNode->next = NULL; //链表结束
} 默认构造函数的时间复杂度为O(1),复制构造函数的时间复杂度为O(theLise.size)。
2.3 析构函数
析构函数要逐个清除链表的结点。实现的策略是重复清除链表的首元素结点,直到链表为空。注意:我们必须在清除首元素结点之前用变量nextNode保存第2个元素结点的指针。析构函数的时间复杂度为O(listSize)
template
chain::~chain()
{//链表的析构函数 删除链表的所有结点
while (firstNode != NULL)
{//删除首结点
chainNode* nextNode = firstNode->next;
delete firstNode;
firstNode = nextNode;
}
}
2.4 方法get
在数组描述的线性表中,我们根据公式来计算一个表元素的位置。然后在链表中,要寻找索引为theIndex的元素,必须从第一个结点开始,跟踪链域next直至找到所需的元素结点指针。也就是说,必须跟踪theIndex个指针。不可能对firstNode套用公式来计算所需结点的位置。
template
void chain::checkIndex(int theIndex) const
{//确定索引在0和listSize-1之间
if (theIndex < 0 || theIndex > listSize - 1)
{
//输出错误
}
}
template
T& chain::get(int theIndex) const
{//返回索引为theIndex的元素
//所该元素不存在,则抛出异常
checkIndex(theIndex);
//移动所需要的结点
chainNode* currentNode = firstNode;
int i;
for (i = 0; i < theIndex; ++i)
{
currentNode = currentNode->next;
return currentNode->element;
}
} 方法get的时间复杂度为O(theIndex),而在数组描述的线性表arrayList中get的时间复杂度为O(1)。
2.5 方法indexOf
如果链表里有迭代器则可以直接用STL中的find函数,那么其代码和arrayList
template
int chain::indexOf(const T& theElement) const
{//返回元素theElement首次出现的索引
//若该元素不存在,则返回-1
//搜索链表元素theElement
chainNode* currentNode = firstNode;
int index = 0;
while (currentNode != NULL && currentNode->element != theElement)
{
currentNode = currentNode->next;
inde++;
}
//判断是否找到元素
if(currentNode == NULL)
{
return -1;
}
else
{
return index;
}
}
2.6 方法erase
单链表的删除
实际上就是一步,p->next = p->next->next. 用p来取代p->next;
q=p->next;
p->next = q->next;
假设链表没有头结点,删除索引为theIndex的元素,考虑以下三种情况:
(1)theIndex<0或者theIndex>=listSize。这时,删除操作无效。
(2)删除非空表的第0个元素的结点。
(3)删除其他元素结点。
template
void chain::erase(int theIndex)
{//删除索引为theIndex的元素
//若此元素不存在,则抛出异常
checkIndex(theIndex);
//索引有效,需找要删除的元素结点
chainNode* deleteNode;
if (theIndex == 0)
{//删除链表的首结点
deleteNode = firstNode;
firstNode = firstNode->next;
}
else
{//用指针p指向要删除结点的前驱结点
chainNode* p = firstNode;
for (int i = 0; i < theIndex - 1; ++i)
p = p -> next;
deleteNode = p->next;
p->next = p->next->next;
}
listSize--;
delete deleteNode;
} chain
假设链表有头结点,删除索引为theIndex的元素,考虑以下二种情况:
(1)theIndex<0或者theIndex>=listSize抛出异常。
(2)删除元素结点
template
void chain::erase(int theIndex)
{//删除索引为theIndex的元素
//若此元素不存在,则抛出异常
checkIndex(theIndex);
//索引有效,需找要删除的元素结点
chainNode* deleteNode;
//用指针p指向要删除结点的前驱结点
chainNode* p = firstNode;
for (int i = 0; i < theIndex; ++i)
p = p -> next;
deleteNode = p->next;
p->next = p->next->next;
listSize--;
delete deleteNode;
} 由此可见,加了头结点是erase方法更统一。同理对insert也一样。
2.7 方法insert
单单链表的插入
若将结点插入结点p和p->next结点之间,只需要做如下变换:
s->next = p->next;
p->next = s;
这两句的顺序是不能改变的。
假设无头结点,插入位置索引为theIndex,分为3中情况:
(1)theIndex<0或者theIndex>0抛出异常。(注意这里和erase并不同)
(2)在第一个结点位置上插入新结点
(3)在其他位置上插入新结点
template
void chain::insert(int theIndex, const T& theElement)
{//在索引为theIndex的位置上插入元素theElement
if (theIndex < 0 || theIndex > listSize)
{//无效索引
//抛出异常
}
if (theIndex == 0)
firstNode = new chainNode(theElement, firstNode);
else
{//寻找新元素的前驱
chainNode* p = firstNode;
for (int i = 0; i < theIndex - 1; ++i)
{
p = p->next;
}
//在p之后插入
p->next = new chainNode(theElement, p->next);
}
listSize++;
} insert的时间复杂度为O(theIndex)
假设有头结点,则分为以下两种情况:
(1)theIndex<0或者theIndex>listSize。抛出异常。
(2)插入新结点
template
void chain::insert(int theIndex, const T& theElement)
{//在索引为theIndex的位置上插入元素theElement
if (theIndex < 0 || theIndex > listSize)
{//无效索引
//抛出异常
}
//寻找新元素的前驱
chainNode* p = firstNode;
for (int i = 0; i < theIndex; ++i)
{
p = p->next;
}
//在p之后插入
p->next = new chainNode(theElement, p->next);
listSize++;
} 对于基本的插入与删除操作,它们其实都是两部分组成:
1.遍历查找第i个结点;
2.插入和删除结点。
2.8 链表与数组的优劣势
(1)空间复杂度:虽然链表在空间上的复杂度要优于数组,但大多数情况下,空间需求上的差异不是决定因素。
(2)时间复杂度:从上述分析,其实链表的性能从各个方法并不如数组。
虽然链表描述得线性表在标准操作的计时实验中表现不好,但是在若干个线性表的应用中,它比数组描述的线性表更有效。如把一个链表的尾结点和另一个链表的首结点链接起来,两个链表可以合并成一个链表,若知道一个链表的首尾结点,合并的用时为O(1)。要把两个数组描述的线性表合并为一个,必须把第二个表复制到第一个表的数值中。这种复制耗时O(size of second list)。当我们知道一个结点的前驱,链表的删除和插入操作用时为O(1);而这种操作在数组描述的线性表中需要用时O(listSize)。
3 循环链表
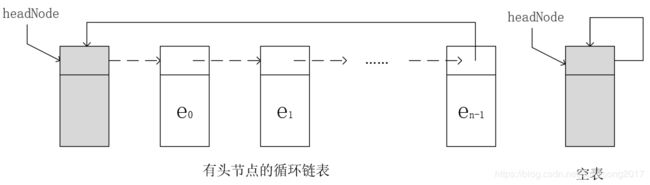
单向循环链表(简称循环链表),只要将单向链表的尾结点与头结点连接起来,单向链表就成为循环链表。(头结点使程序更为方便简洁,运行速度更快)
无头结点的循环链表
3.1 搜索带有头结点的循环链表
template
circularListWithHeader::circularListWithHeader()
{//构造函数
headerNode = new chainNode();
headerNode->next = headerNode;
listSize = 0;
}
template
int circularListWithHeader::indexOf(const T& theElement) const
{//返回元素theElement首次出现的索引
//若该元素不存在,则返回-1
//将元素theElement放入头结点
headerNode->element = theElement;
//在链表中搜索元素theElement
chainNode* currentNode = headerNode->next;
int index = 0; //当前结点的索引
while (currentNode->element != theElement)
{
//移动到下一个结点
currentNode = currentNode->next;
index++;
}
//确定是否找到元素theElement
if (currentNode == headerNode)
return -1;
else
return index;
}
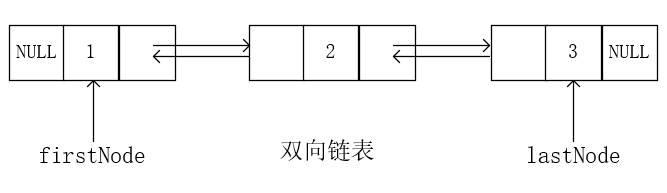
4 双向链表
双向链表:每个结点既有一个指向后继的指针next,又有一个指向前驱的指针previous。next指向右边的结点(如果存在),previous指针指向左边结点(如果存在)。
5 参考文献
1 《大话数据结构》 程杰著.
2 《数据结构、算法与应用(C++语言秒杀你)》 Sartaj Sahni著.