【图解例说机器学习】神经网络 (Neural Networks)
神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。 --Kohonen, 1988
一层神经网络:感知机与逻辑回归
M-P神经元模型
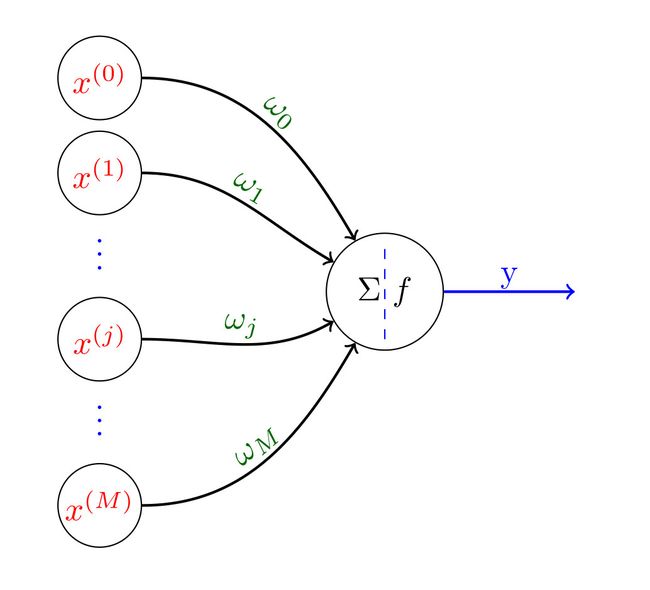
1943年,McCulloch和Pitts提出了沿用至今的M-P神经元。在这个模型中,神经元接收来自其他 M M M个神经元传递过来的输入信号 x ( j ) , j = 1 , 2 , ⋯ , M x^{(j)},j=1,2,\cdots,M x(j),j=1,2,⋯,M, 这些输入信号通过带权重 ω j \omega_j ωj的连接进行传递,神经元接收到总输入值与神经元的阈值进行比较,然后通过激活函数处理以产生神经元的输出。
根据上述M-P神经元模型的定义,我们可以通过图1形象地表示该模型:(注意:文中所有图像使用Tikz或者Python绘制。由于篇幅有限,具体代码实现在【漫漫科研路\Python&Tikz】画神经网络相关图给出)
|
M-P神经元的数学表达式也可以表示如下:
y = f ( ∑ j = 1 M ω j x ( j ) + ω 0 ) (1) y=f(\sum\limits_{j=1}^{M}\omega_jx^{(j)}+\omega_0)\tag{1} y=f(j=1∑Mωjx(j)+ω0)(1)
注意:这里我们假设 x ( 0 ) = 1 , w = { ω 1 , ω 2 , ⋯ , ω M } , w ˉ = { ω 0 , w } x^{(0)}=1, \mathrm w=\{\omega_1,\omega_2,\cdots,\omega_M\}, \bar{\mathrm w}=\{\omega_0,\mathrm w\} x(0)=1,w={ω1,ω2,⋯,ωM},wˉ={ω0,w}。那么公式(1)也可以写成向量的形式:
y = f ( ∑ j = 0 M ω j x ( j ) ) = f ( w ˉ T x ) y=f(\sum\limits_{j=0}^{M}\omega_jx^{(j)})=f(\bar{\mathrm w}^{\mathrm T}\mathrm x) y=f(j=0∑Mωjx(j))=f(wˉTx)
感知机与逻辑回归
前面系列文章中介绍的感知机和逻辑回归就是M-P神经元模型的两个具体实例。这两者的区别在于:
-
激活函数:感知机使用的是阶跃函数,逻辑回归使用的Sigmoid函数,如图2所示:
 图2
图2
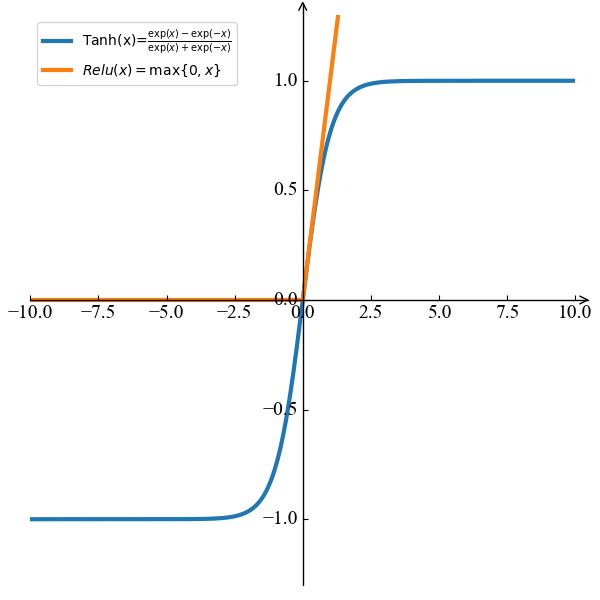 图3
图3
同时,最近比较流行的激活函数还有 t a n h tanh tanh 和 R e l u Relu Relu 函数,如图3所示。
-
损失函数:感知机使用的是错误分类点到分类超平面距离最小化,逻辑回归使用的交叉熵最小化
感知机和逻辑回归是一个最简单的一层神经网络,只有一个神经元(M-P神经元),可以看成是所有神经网络的基础。注意:这里对于神经网络的层数有不同的定义,主要区别在于是否将输入层看作一层神经网络。这里我们不把输入层看成一层神经网络,只将具有功能神经元(有激活函数)的输出层看成一层神经网络,因此感知机和逻辑回归是一层神经网络,而不是二层神经网络。
前面文章我们已经介绍过,标准的感知机和逻辑回归模型只能解决线性可分的问题,这是因为它们都只有一个M-P神经元,模型较为简单。为了解决线性不可分问题,我们需要考虑更为复杂的模型,比如考虑使用多层神经网络。下面我们来举例说明通过增加神经网络层数来解决线性不可分的问题(例如:如前面文章SVM中提到的异或问题)。
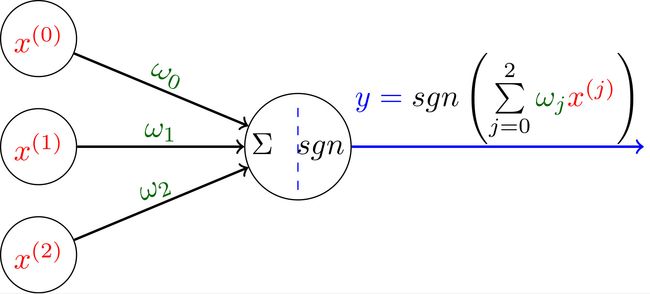 图4 图4
|
 图5 图5
|
图4是一个感知机的图解模型,其激活函数为图2所示的符号函数 s g n sgn sgn。我们知道,感知机只能处理线性可分的情况,比如常见的与、或、非计算。具体实现如下所示:
- 与计算 :令 ω 1 = ω 2 = 1 , ω 0 = − 2 \omega_1=\omega_2=1,\omega_0=-2 ω1=ω2=1,ω0=−2,我们有 y = s g n ( x ( 1 ) + x ( 2 ) − 2 ) y=sgn(x^{(1)}+x^{(2)}-2) y=sgn(x(1)+x(2)−2)。此时,只有当 x ( 1 ) = x ( 2 ) = 1 x^{(1)}=x^{(2)}=1 x(1)=x(2)=1时, y = 1 y=1 y=1
- 或计算:令 ω 1 = ω 2 = 1 , ω 0 = − 0.5 \omega_1=\omega_2=1,\omega_0=-0.5 ω1=ω2=1,ω0=−0.5,我们有 y = s g n ( x ( 1 ) + x ( 2 ) − 0.5 ) y=sgn(x^{(1)}+x^{(2)}-0.5) y=sgn(x(1)+x(2)−0.5)。此时,当 x ( 1 ) = 1 x^{(1)}=1 x(1)=1或者 x ( 2 ) = 1 x^{(2)}=1 x(2)=1时, y = 1 y=1 y=1
- 非计算:令 ω 1 = − 0.6 \omega_1=-0.6 ω1=−0.6, ω 2 = 0 , ω 0 = 0.5 \omega_2=0,\omega_0=0.5 ω2=0,ω0=0.5,我们有 y = s g n ( − 0.6 x ( 1 ) + 0.5 ) y=sgn(-0.6x^{(1)}+0.5) y=sgn(−0.6x(1)+0.5)。此时,当 x ( 1 ) = 0 x^{(1)}=0 x(1)=0时, y = 1 y=1 y=1; 当 x ( 1 ) = 1 x^{(1)}=1 x(1)=1时, y = 0 y=0 y=0
当我们需要处理线性不可分的情况时(如异或问题),我们可以考虑在图4的基础上加入一层神经元,如图5所示。在图5中,我们令 ω 01 ( 1 ) = ω 02 ( 1 ) = ω 2 ( 2 ) = − 0.5 \omega_{01}^{(1)}=\omega_{02}^{(1)}=\omega_2^{(2)}=-0.5 ω01(1)=ω02(1)=ω2(2)=−0.5, ω 11 ( 1 ) = ω 22 ( 1 ) = ω 1 ( 2 ) = ω 2 ( 2 ) = 1 \omega_{11}^{(1)}=\omega_{22}^{(1)}=\omega_1^{(2)}=\omega_2^{(2)}=1 ω11(1)=ω22(1)=ω1(2)=ω2(2)=1, ω 12 ( 1 ) = ω 21 ( 1 ) = − 1 \omega_{12}^{(1)}=\omega_{21}^{(1)}=-1 ω12(1)=ω21(1)=−1, 这时候我们有
y = s g n [ s g n ( x ( 1 ) − x ( 2 ) − 0.5 ) + s g n ( x ( 2 ) − x ( 1 ) − 0.5 ) − 0.5 ] (2) y=sgn[sgn(x^{(1)}-x^{(2)}-0.5)+sgn(x^{(2)}-x^{(1)}-0.5)-0.5]\tag{2} y=sgn[sgn(x(1)−x(2)−0.5)+sgn(x(2)−x(1)−0.5)−0.5](2)
由公式(2)可以看出,当 x ( 1 ) = x ( 2 ) x^{(1)}=x^{(2)} x(1)=x(2)时, y = 0 y=0 y=0; 当 x ( 1 ) ≠ x ( 2 ) x^{(1)}\neq x^{(2)} x(1)=x(2)时, y = 1 y=1 y=1。我们可以根据公式(2),画出其分类区域,如下图6所示:
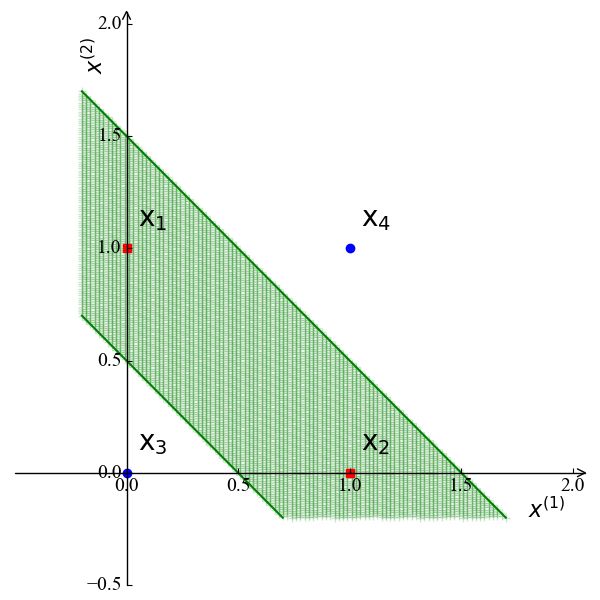 图6 图6
|
 图7 图7
|
在图6中,位于两条绿色直线之间所有区域 (例如:绿色区域) 都被归于同一类。我们发现通过添加一层神经元,我们就可以处理线性不可分的情况。实际上,这一层神经元的功能就是将输入的特征空间 x ( 1 ) , x ( 2 ) x^{(1)},x^{(2)} x(1),x(2)映射到了新的特征空间 z ( 1 ) , z ( 2 ) z^{(1)},z^{(2)} z(1),z(2),而新的特征空间线性可分,如图7所示。其中这4个样例点映射到新的特征空间,其映射关系为 x 1 → z 1 , x 2 → z 2 , x 3 , 4 → z 3 , 4 ( 0 , 0 ) \mathrm x_1\rightarrow\mathrm z_1, \mathrm x_2\rightarrow\mathrm z_2, \mathrm x_{3,4}\rightarrow\mathrm z_{3,4} (0,0) x1→z1,x2→z2,x3,4→z3,4(0,0)。可见,在该新的特征空间,样例点线性可分。
两层神经网络–BP 神经网络
实际上,理论证明,两层神经网络可以拟合任何复杂形式的函数表达上。为此,本文主要介绍经典的两层前馈神经网络 (相邻层神经元全连接,神经元之间不存在同层连接,也不存在夸层连接),如图8所示。
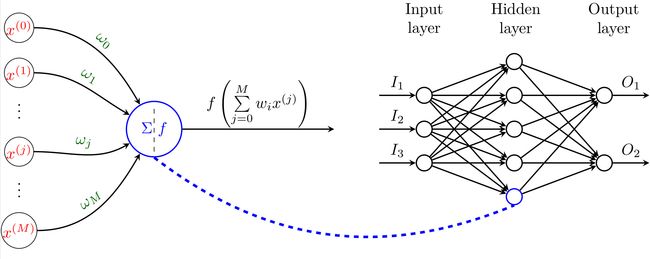
|
在图8中,经典的神经网络由输入层、隐藏层、输出层组成,其中隐藏层和输出层的每一个神经元都是我们前面介绍的M-P神经元。我们发现,神经网络由多层多个神经元构成,其学习算法肯定比感知机和逻辑回归复杂。下面我们介绍神经网络中最常用的BP (BackPropagation) 算法。
信号前向传播
在介绍BP算法时,我们需要了解神经网络的结构所决定的输入与输出间的关系表达式,即所谓的输入信号如何向前传播的输出端的。这里我们用图9可以完全形象地描述这一信息流的传播过程:

|
在图9中,我们假设输入层、隐藏层、输出层的神经元个数分别为 I , J , K I,J,K I,J,K,激活函数 σ \sigma σ选择为Sigmoid函数。 α ( j ) , β ( k ) \alpha^{(j)},\beta^{(k)} α(j),β(k)分别为隐藏层和输出层的第 j , k j,k j,k个神经元的输入; z ( j ) , y ^ ( k ) z^{(j)},\hat y^{(k)} z(j),y^(k)分别为隐藏层和输出层的第 j , k j,k j,k个神经元的输出。注意:这里我们有 x ( 0 ) = z ( 0 ) = 1 x^{(0)}=z^{(0)}=1 x(0)=z(0)=1是为了让求和的下标从0开始,此时对应的权重就是其他文章所说的阈值。图9的右侧给出了所有可能的输入输出的关系表达式。
误差反向传播
BP算法的核心就是误差反向传播。这里我们定义一个输入样例 x \mathrm x x对应的误差为:
E = 1 2 ∑ k = 1 K ( y ^ ( k ) − y ( k ) ) 2 (3) E=\frac{1}{2}\sum\limits_{k=1}^{K}(\hat y^{(k)}-y^{(k)})^2\tag{3} E=21k=1∑K(y^(k)−y(k))2(3)
公式(3)中 y ( k ) y^{(k)} y(k)为样例 x \mathrm x x的实际输出 y y y的第 k k k个输出。注意:这里的误差是一个样例的误差,而不是所有训练样例的误差。
BP算法的目的是优化权重 ω i j ( 1 ) , ω j k ( 2 ) \omega_{ij}^{(1)},\omega_{jk}^{(2)} ωij(1),ωjk(2)来最小化误差 E E E。为此,BP算法采用了和梯度下降法一样的思想,以误差对权重的负梯度方向来不断更新权重,降低误差 E E E。为此,我们需要计算输出层和隐藏层的 ∂ E ∂ ω i j ( 1 ) \frac{\partial E}{\partial\omega_{ij}^{(1)}} ∂ωij(1)∂E和 ∂ E ∂ ω j k ( 2 ) \frac{\partial E}{\partial\omega_{jk}^{(2)}} ∂ωjk(2)∂E。
输出层梯度
利用链式法则,我们有:
∂ E ∂ ω j k ( 2 ) = ∂ E ∂ y ^ ( k ) ∂ y ^ ( k ) ∂ β ( k ) ∂ β ( k ) ∂ ω j k ( 2 ) (4) \frac{\partial E}{\partial\omega_{jk}^{(2)}}=\frac{\partial E}{\partial \hat y^{(k)}}\frac{\partial\hat y^{(k)}}{\partial\beta^{(k)}}\frac{\partial\beta^{(k)}}{\partial \omega_{jk}^{(2)}}\tag{4} ∂ωjk(2)∂E=∂y^(k)∂E∂β(k)∂y^(k)∂ωjk(2)∂β(k)(4)
对于公式(4)中等式右边的每一项,我们有:
∂ E ∂ y ^ ( k ) = ∂ 1 2 ∑ k = 1 K ( y ^ ( k ) − y ( k ) ) 2 ∂ y ^ ( k ) = y ^ ( k ) − y ( k ) (5) \frac{\partial E}{\partial\hat y^{(k)}}=\frac{\partial \frac{1}{2}\sum\limits_{k=1}^{K}(\hat y^{(k)}-y^{(k)})^2}{\partial\hat y^{(k)}}=\hat y^{(k)}-y^{(k)}\tag{5} ∂y^(k)∂E=∂y^(k)∂21k=1∑K(y^(k)−y(k))2=y^(k)−y(k)(5)
∂ y ^ ( k ) ∂ β ( k ) = ∂ s i g m o i d ( β ( k ) ) ∂ β ( k ) = y ^ ( k ) ( 1 − y ^ ( k ) ) (6) \frac{\partial\hat y^{(k)}}{\partial\beta^{(k)}}=\frac{\partial sigmoid(\beta^{(k)})}{\partial\beta^{(k)}}=\hat y^{(k)}(1-\hat y^{(k)})\tag{6} ∂β(k)∂y^(k)=∂β(k)∂sigmoid(β(k))=y^(k)(1−y^(k))(6)
∂ β ( k ) ∂ ω j k ( 2 ) = ∂ ∑ j = 0 J ω j k ( 2 ) z ( j ) ∂ ω j k ( 2 ) = z ( j ) (7) \frac{\partial\beta^{(k)}}{\partial\omega_{jk}^{(2)}}=\frac{\partial\sum\limits_{j=0}^{J}\omega_{jk}^{(2)}z^{(j)}}{\partial\omega_{jk}^{(2)}}=z^{(j)}\tag{7} ∂ωjk(2)∂β(k)=∂ωjk(2)∂j=0∑Jωjk(2)z(j)=z(j)(7)
在公式(6)中,第二个等式成立是因为对于sigmoid函数,例如 y = f ( x ) y=f(x) y=f(x),其导数为 y ′ = y ( 1 − y ) y^\prime=y(1-y) y′=y(1−y)。综合(5)-(7),公式(4)可以写为:
∂ E ∂ ω j k ( 2 ) = y ^ ( k ) ( 1 − y ^ ( k ) ) ( y ^ ( k ) − y ( k ) ) z ( j ) = g ( k ) z ( j ) (8) \frac{\partial E}{\partial\omega_{jk}^{(2)}}=\hat y^{(k)}(1-\hat y^{(k)})(\hat y^{(k)}-y^{(k)})z^{(j)}=g^{(k)}z^{(j)}\tag{8} ∂ωjk(2)∂E=y^(k)(1−y^(k))(y^(k)−y(k))z(j)=g(k)z(j)(8)
在公式(8)中,为了简便起见,我们令
g ( k ) = y ^ ( k ) ( 1 − y ^ ( k ) ) ( y ^ ( k ) − y ( k ) ) (9) g^{(k)}=\hat y^{(k)}(1-\hat y^{(k)})(\hat y^{(k)}-y^{(k)})\tag{9} g(k)=y^(k)(1−y^(k))(y^(k)−y(k))(9)
隐藏层梯度
与上面计算过程类似,下面我们计算 ∂ E ∂ ω i j ( 1 ) \frac{\partial E}{\partial\omega_{ij}^{(1)}} ∂ωij(1)∂E。同样地,利用链式法则,我们有:
∂ E ∂ ω i j ( 1 ) = ∂ E ∂ z ( j ) ∂ z ( j ) ∂ α ( j ) ∂ α ( j ) ∂ ω i j ( 1 ) (10) \frac{\partial E}{\partial\omega_{ij}^{(1)}}=\frac{\partial E}{\partial z^{(j)}}\frac{\partial z^{(j)}}{\partial\alpha^{(j)}}\frac{\partial\alpha^{(j)}}{\partial\omega_{ij}^{(1)}}\tag{10} ∂ωij(1)∂E=∂z(j)∂E∂α(j)∂z(j)∂ωij(1)∂α(j)(10)
对于公式(10)中等式右边的每一项,我们有:
∂ E ∂ z ( j ) = ∑ k = 0 K ∂ E ∂ β ( k ) ∂ β ( k ) ∂ z ( j ) = ∑ k = 0 K ∂ E ∂ y ^ ( k ) ∂ y ^ ( k ) ∂ β ( k ) ∂ β ( k ) ∂ z ( j ) = ∑ k = 0 K g ( k ) ω j k ( 2 ) (11) \frac{\partial E}{\partial z^{(j)}}=\sum\limits_{k=0}^{K}\frac{\partial E}{\partial\beta^{(k)}}\frac{\partial\beta^{(k)}}{\partial z^{(j)}}=\sum\limits_{k=0}^{K}\frac{\partial E}{\partial\hat y^{(k)}}\frac{\partial\hat y^{(k)}}{\partial\beta^{(k)}}\frac{\partial\beta^{(k)}}{\partial z^{(j)}}=\sum\limits_{k=0}^{K}g^{(k)}\omega_{jk}^{(2)}\tag{11} ∂z(j)∂E=k=0∑K∂β(k)∂E∂z(j)∂β(k)=k=0∑K∂y^(k)∂E∂β(k)∂y^(k)∂z(j)∂β(k)=k=0∑Kg(k)ωjk(2)(11)
∂ z ( j ) ∂ α ( j ) = ∂ S i g m o i d ( α ( j ) ) ∂ α ( j ) = z ( j ) ( 1 − z ( j ) ) (12) \frac{\partial z^{(j)}}{\partial\alpha^{(j)}}=\frac{\partial Sigmoid(\alpha^{(j)})}{\partial\alpha^{(j)}}=z^{(j)}(1-z^{(j)})\tag{12} ∂α(j)∂z(j)=∂α(j)∂Sigmoid(α(j))=z(j)(1−z(j))(12)
∂ α ( j ) ∂ ω i j ( 1 ) = ∂ ∑ i = 1 I ω i j ( 1 ) x ( i ) ∂ ω i j ( 1 ) = x ( i ) (13) \frac{\partial\alpha^{(j)}}{\partial\omega_{ij}^{(1)}}=\frac{\partial\sum\limits_{i=1}^{I}\omega_{ij}^{(1)}x^{(i)}}{\partial\omega_{ij}^{(1)}}=x^{(i)}\tag{13} ∂ωij(1)∂α(j)=∂ωij(1)∂i=1∑Iωij(1)x(i)=x(i)(13)
综合(11)-(13),公式(10)可以写成:
∂ E ∂ ω i j ( 1 ) = x ( i ) z ( j ) ( 1 − z ( j ) ) ∑ k = 0 K g ( k ) ω j k ( 2 ) (14) \frac{\partial E}{\partial\omega_{ij}^{(1)}}=x^{(i)}z^{(j)}(1-z^{(j)})\sum\limits_{k=0}^{K}g^{(k)}\omega_{jk}^{(2)}\tag{14} ∂ωij(1)∂E=x(i)z(j)(1−z(j))k=0∑Kg(k)ωjk(2)(14)
梯度迭代法则
求得输出层和隐藏层的梯度(8)和(14)后,我们就可以利用最常见的负梯度迭代法来更新权重:
ω i j ( 1 ) = ω i j ( 1 ) − η ∂ E ∂ ω i j ( 1 ) (15) \omega_{ij}^{(1)}=\omega_{ij}^{(1)}-\eta\frac{\partial E}{\partial\omega_{ij}^{(1)}}\tag{15} ωij(1)=ωij(1)−η∂ωij(1)∂E(15)
ω j k ( 2 ) = ω i j ( 2 ) − η ∂ E ∂ ω j k ( 2 ) (16) \omega_{jk}^{(2)}=\omega_{ij}^{(2)}-\eta\frac{\partial E}{\partial\omega_{jk}^{(2)}}\tag{16} ωjk(2)=ωij(2)−η∂ωjk(2)∂E(16)
至此,标准的BP算法就已经介绍完成了:不断地根据(15)-(16)更新权值,直到不再改变。注意:我们前面已经提到,这里的误差 E E E是对于单个训练样例的,即每来一次新的样例,我们就得更新权值。当然,我们可以一次性考虑所有的训练样例,即此时的误差函数为所有训练样例的误差加和,这时的算法称为累积BP算法。
多层神经网络–深度学习
从理论上来说,神经网络的神经元越多,层数越多,模型的复杂度越高,能完成更加复杂的学习任务。但是一般情况下,模型的复杂度高意味着训练效率低,容易出现过拟合。随着计算能力的提高,以深度学习为代表的复杂神经网络开始变得越来越流行。深度学习模型就是一个深层的神经网络。关于深度学习,会在后续系列文章中介绍,这里不再展开。