Coursera deeplearning.ai 深度学习笔记2-2-Optimization algorithms-优化算法与代码实现

1. 优化算法

1.1 小批量梯度下降(Mini-batch Gradient Descent)

对于很大的训练集m，可以将训练集划分为T个mini-batch，分批量来学习，这样将第t个mini-batch的参数定义为X^{t}、Y^{t}。训练流程如下：
fort=1,…,TforwardpropagationonX{t},computecostJ{t},backwardpropagationtocomputedW[l],db[l],gradientdescentW[l]=W[l]−αdW[l],b[l]=b[l]−αdb[l](1)
如果mini-batch的大小为m，也就是批量梯度下降(Gradient Descent)，参数会沿着梯度最大的方向迭代，代价函数不断下降，但是每次迭代花费的时间较长。
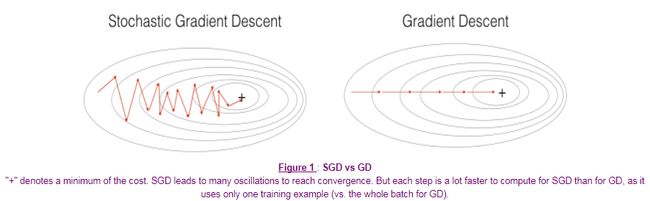
如果mini-batch的大小为1，也就是随机梯度下降(Stochastic Gradient Descent)，其中的噪声较多，代价函数会呈波动下降的趋势，不过失去了向量化所带来的计算优势。
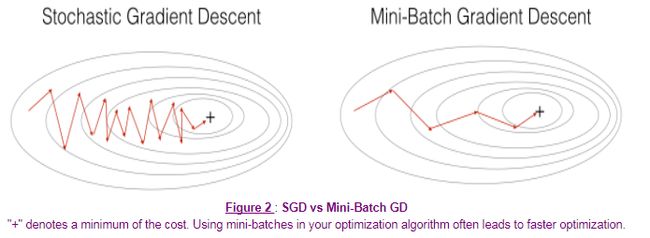
选取合适的mini-batch大小，能够减少迭代花费的时间，同时将向量化计算的优势也发挥出来。并不能保证每次都能得到代价函数的最小值，但是比随机梯度下降的噪声更小。
Mini-batch大小的选取：如果训练集较小(m < 2000)，就使用批量梯度下降法；否则，可以将mini-batch的大小设置为64、128、256、512等。

1.2 动量梯度下降(Gradient Descent with Momentum)

在梯度下降时，波动可能较小，而动量梯度下降的思想是，采用指数加权平均，使得每次梯度下降更加平滑，具体如下：
VdW=β1VdW+(1−β1)dWVdb=β1Vdb+(1−β1)dbW=W−αVdW,b=b−αVdb(2)
上式中，初始化V_dW = 0，V_db = 0。如果β₁ = 0，就等效于梯度下降。实践中，β₁ = 0.9是比较稳健的数值，也可以选择其他数值。

1.3 均方根传递(RMS Prop, Root Mean Square Prop)

在梯度下降时，例如dW较小、db较大的情况，希望减慢b方向的学习，同时加快或者不减慢W方向的学习，可以采用均方根传递如下：
SdW=β2SdW+(1−β2)dW2Sdb=β2Sdb+(1−β2)db2W=W−αdWSdW√+ε,b=b−αdbSdb√+ε(3)
上式中，dW²和db²为元素点乘，参数ε为小量(例如10^-8)，避免分母接近0。式中，由于dW较小、db较大，则S_dW项较小、S_db项较大，即S_dW项的倒数较大、S_db项的倒数较小，从而能够减慢b方向的学习，而加快W方向的学习。

1.4 Adam算法(Adaptive Moment Estimation)

Adam算法将动量梯度下降和均方根传递结合起来，同时需要进行适当修正，具体如下：
VdW=0,SdW=0,Vdb=0,Sdb=0interationt:computedW,dbusingmini−batchVdW=β1VdW+(1−β1)dW,Vdb=β1Vdb+(1−β1)db⇐Momemtum:β1SdW=β2SdW+(1−β2)dW2,Sdb=β2Sdb+(1−β2)db2⇐RMSProp:β2VcorrecteddW=VdW1−βt1,Vcorrecteddb=Vdb1−βt1,ScorrecteddW=SdW1−βt2,Scorrecteddb=Sdb1−βt2W=W−αVcorrecteddWScorrecteddW√+ε,b=b−αVcorrecteddbScorrecteddb√+ε(4)
超参数的一些推荐值如下：
β1=0.9,β2=0.999,ε=10−8(5)
学习因子α仍然需要调整。

1.5 学习因子衰减(Learning Rate Decay)

最终收敛数值取决于学习因子的大小，因此，逐渐降低学习因子有利于收敛到更优的数值。学习因子衰减，就是在学习开始时采用较小的步长，当学习开始收敛一些时采取更小的步长。将学习因子写成：
α=11+decay_rate∗epoch_numα0(6)
式中，decay_rate为衰减率，epoch_num为迭代次数，α₀为初始学习因子。随着迭代次数的增加，学习因子就会不断降低。
此外，还有一些其他的学习因子衰减算法，例如：
α=0.95epoch−numα0α=kepoch−num√α0(7)

1.6 局部最优

在神经网络中，由于训练的参数较多，不容易陷入局部最优，而是可能遇到鞍点(Saddle Point)。

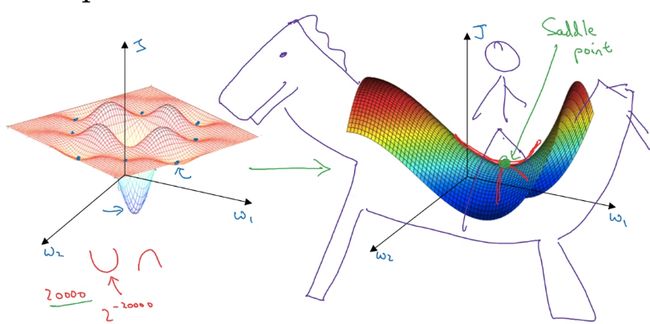
真正会降低学习速度的是停滞区(Plateaus)，是指导数长时间接近于零的一个区域。

2. 代码实现

案例：对蓝点和红点进行二分类，研究不同优化算法对结果的影响。

2.1 梯度下降update_parameters_with_gd

首先实现不采用任何优化算法的梯度下降：
W=W−αdW,b=b−αdb(8)
核心代码如下：

2.2 Mini-batch梯度下降random_mini_batches

实现mini-batch梯度下降分为两步：
(1) Shuffle随机排序：对序列X和Y的每一列进行随机排序，注意X和Y的随机打乱要同步。

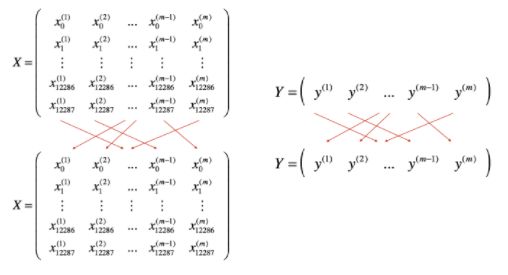
(2) Partition分割：将默认mini-batch的大小设置为64，对随机排序后的X和Y进行分割，注意最后一组数据可能小于默认的mini-batch大小。

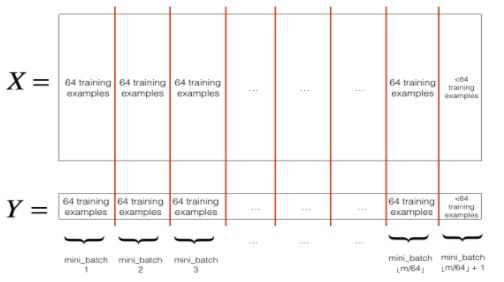
核心代码如下：

2.3 Momentum梯度下降update_parameters_with_momentum

采用下式实现Momentum梯度下降，将V_dW和V_db初始化为0：
VdW=β1VdW+(1−β1)dWVdb=β1Vdb+(1−β1)dbW=W−αVdW,b=b−αVdb(9)
参数β₁为0时，就相当于不使用Momentum的梯度下降。β₁越大，平滑效果越好，通常取在0.8 ~ 0.999之间，0.9是一个比较合理的数值。
核心代码如下：

2.4 Adam算法update_parameters_with_adam

Adam算法综合了Momentum和RMS Drop算法，将V_dW、V_db和S_dW、S_db初始化为0，如下：
VdW=β1VdW+(1−β1)dW,Vdb=β1Vdb+(1−β1)dbVcorrectddW=VdW1−βt1,Vcorrectddb=Vdb1−βt1SdW=β2SdW+(1−β2)dW2,Sdb=β2Sdb+(1−β2)db2ScorrectddW=SdW1−βt2,Scorrectddb=Sdb1−βt2W=W−αVcorrecteddWScorrecteddW√+ε,b=b−αVcorrecteddbScorrecteddb√+ε(10)
核心代码如下：

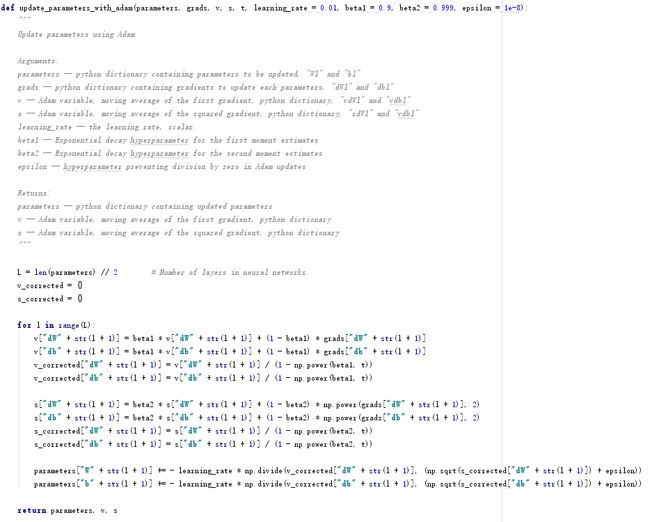
2.5 模型训练model

分别采用三种算法进行模型训练，核心代码如下：

2.6 不同优化算法结果对比

测试核心代码如下：

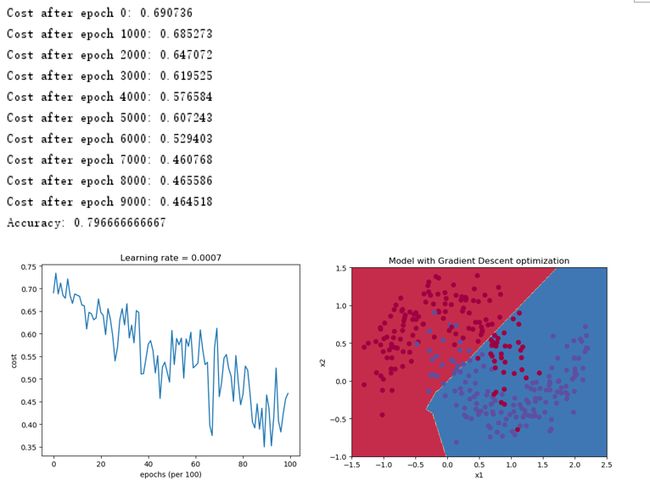
2.6.1 mini-batch梯度下降

采用mini-batch梯度下降得到如下结果，可以看出，代价函数的波动较大。

2.6.2 mini-batch + momentum梯度下降

采用mini-batch + momentum梯度下降得到如下结果，由于案例比较简单，momentum的优势没有体现出来，对于比较复杂的案例，momentum是能够由一定的性能提升的。

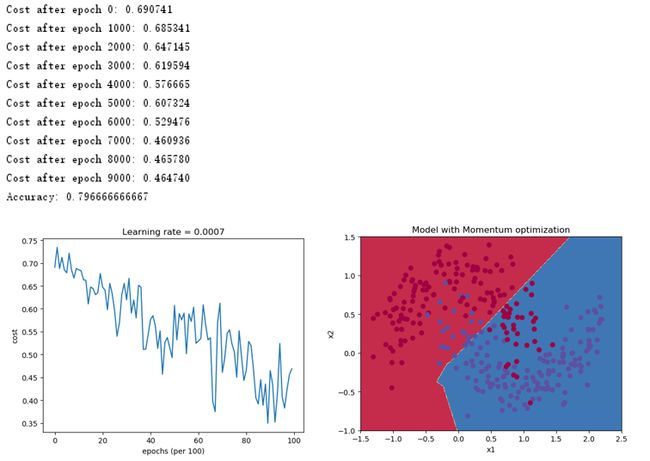
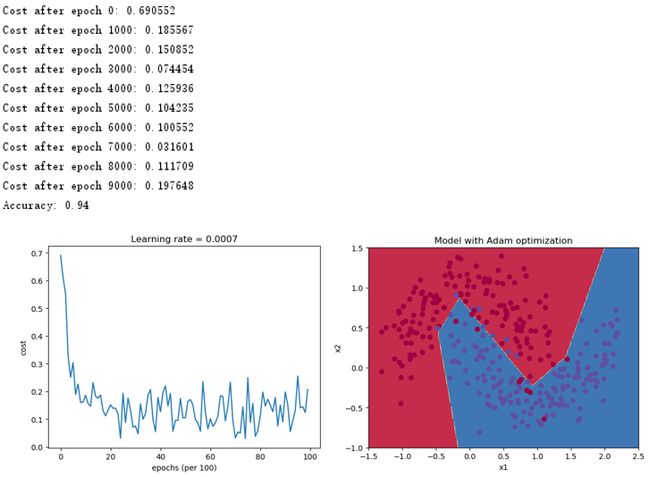
2.6.3 mini-batch + Adam梯度下降

采用mini-batch + Adam梯度下降得到如下结果，可以看出，代价函数的波动明显降低，收敛更快，能够得到更好的准确率94%。

2.6.4 总结

如果训练足够长时间，三种优化算法均能够得到较好的效果。不过对于此案例，Adam算法明显提升了收敛速度。

优化算法	准确率	代价函数
Mini-batch	79.7%	波动大
Mini-batch + Momentum	79.7%	波动大
Mini-batch + Adam	94%	波动平滑

代码下载地址： https://gitee.com/tuzhen301/Coursera-deeplearning.ai2-2