NetworkX 算法列表
官方网站: http://networkx.github.io/
3 Algorithms
3.1 Approximations and Heuristics 近似和启发式算法
3.1.1 Connectivity 连接性
对节点连接性进行快速近似。
连接性是将两个节点断开连接需要删除的最少节点数量。
3.1.2 K-components K组件
K组件是G拥有的节点连接性 ≥ \ge ≥k的最大子图
3.1.3 Clique 分团
计算最大的团(clique)。团是无向图顶点的子集C, C中所有顶点都有边相连。
3.1.4 Clustering 聚类
估计图G的平均聚类系数。
3.1.5 Dominating Set 支配集
寻找节点和边的支配集。
无向图G的支配集是节点的子集D,D外的节点至少与1个D内的节点相邻。
3.1.6 Independent Set 独立(顶点)集
两两不相邻的顶点组成的集合。
3.1.7 Matching 匹配
独立边集。
3.1.8 Ramsey ?
In the language of graph theory, the Ramsey number is the minimum number of vertices such that all undirected simple graphs of order contain a clique of order or an independent set of order . Ramsey’s theorem states that such a number exists for all and .
Ramsey数是最小顶点数量, 使得所有无向简单图都包含…
3.1.9 Steiner Tree (Problem) ?
3.1.10 Treewidth 树宽
无向图的树宽是与这个图相关的数字,是最大顶点集合(bag)的大小…
3.1.11 Vertex Cover 顶点覆盖
计算最近似的最小加权顶点覆盖度。
顶点覆盖度是节点的子集,使得图中的每一条边都能连接到该子集。
3.2 Assortativity 同类性
3.2.1 Assortativity 同类性
计算图的度的同类性。
同类性衡量图中节点的度的连接的相似性。
For instance, in social networks, nodes tend to be connected with other nodes with similar degree values. This tendency is referred to as assortative mixing, or assortativity.
例如,在社交网络中,节点倾向于与度数相近的节点连接,这种倾向称为assortative mixing或Assortativity(协调性)。
3.2.2 Average neighbor degree 平均邻居度
返回每个节点的邻居节点的度的平均值。
3.2.3 Average degree connectivity 平均度连接性
计算图的平均度连接性。
平均度连接性是平均最近邻居的度。对于节点 i i i, k n n , i w = 1 s i ∑ j ∈ N ( i ) w i j k j k_{nn,i}^w=\frac{1}{s_i}\sum_{j\in N(i)}w_{ij}k_j knn,iw=si1∑j∈N(i)wijkj。其中 s i s_i si是节点 i i i的度, w i j w_{ij} wij是 i i i和 j j j之间的边的权重, N ( i ) N(i) N(i)是节点 i i i的邻居节点。
3.2.4 Mixing 混合
属性混合矩阵;度混合矩阵;数值混合矩阵;度混合词典;混合词典
3.3 Bipartite 二分图
本模块提供二分图的函数和操作。
3.3.1 基本函数
是否是二分图, 节点
…
3.4 Boundary 边界
查找一组节点的边界
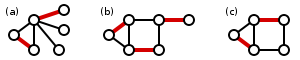
3.5 Bridges 桥发现算法
如果去掉一条边会让图分隔开,这条边就是桥。
3.6 Centrality 中心性
3.6.1 Degree 度中心性
节点的度中心性=度÷{图n-1最大可能的度}, n是图的节点数量。
3.6.2 Eigenvector 特征向量
3.6.3 Closeness 紧密度
节点和图中其它节点之间最短路径的平均值。 C ( x ) = 1 ∑ y d ( y , x ) C(x)=\frac{1}{\sum_yd(y,x)} C(x)=∑yd(y,x)1
3.6.4 Current Flow Closeness 当前流量中心度
把边当成电阻,节点是电阻之间的节点。
3.6.5 (Shortest Path) Betweenness (最短路径)介数
介数中心性
3.7 Chains 链
链是顶点和边的交替序列。
3.8 Chordal 弦图
弦图:构成循环的4个顶点有一个弦。也被称为三角图。
3.9 Clique
3.10 Clustering 聚类
计算三角形的个数,计算聚类系数
3.11 Coloring 图着色问题(相邻节点不同颜色)
3.12 Communicability 传染性
图G中所有节点对之间的传染性是指
3.13 Communities 社团结构
3.14 Components 组件
可以直接统计出各种孤立子网。
3.15 Connectivity 连通性和切割算法
3.15.1 Edge-augmentation 边增强
k-边增强是,添加一组边,使得图是k-边连接的(删除 ≥ k \ge k ≥k条边才能将图分开)。找到这一组具有最小weight的这样一组边。
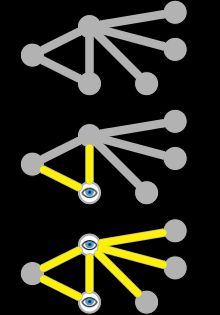
3.16 Cores 内核
Find the k-cores of a graph. 找到图的k-内核。
The k-core is found by recursively pruning nodes with degrees less than k. 通过递归地删除度数小于k的节点找到内核。
3.17 Covering 覆盖图
如果从存在C的顶点集合到G的顶点集合的映射,则C是G的覆盖图。
3.18 Cycles 循环
寻找有向图中的环。
3.19 Cuts 切割
3.20 Directed Acyclic Graphs 有向无环图
拓扑排序,传递闭包
3.21 Dispersion 分散度
3.22 Distance Measures 距离测量
图形直径,半径,偏心率等属性。
3.23 Distance-Regular Graphs 距离规则的图
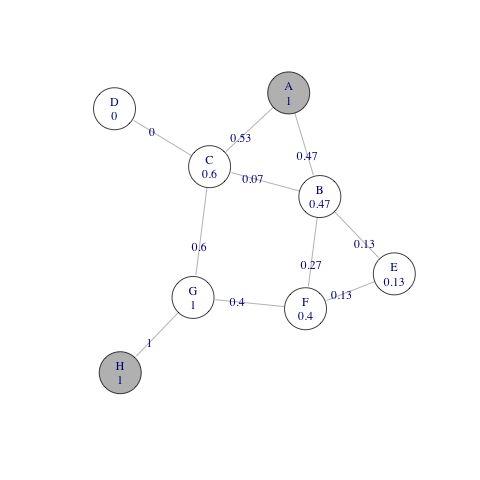
3.24 Dominance 控制
在控制流图中,如果从起点到达n必须经过d,则d控制着n。下图中
3.25 Dominating Sets 控制集
3.26 Efficiency 效率
效率用来衡量交换信息的效率。
3.26.1 两个节点之间的效率
是两节点的最短路径的倒数。
3.26.2 local efficiency
平均效率 E ( G ) = 1 n ( n − 1 ) ∑ i ≠ j ∈ G 1 d ( i , j ) E(G)=\frac{1}{n(n-1)}\sum_{i \neq j \in G}\frac{1}{d(i,j)} E(G)=n(n−1)1∑i̸=j∈Gd(i,j)1,其中 d ( i , j ) d(i,j) d(i,j)是两个节点之间的最短路径。
E g l o b ( G ) = E ( G ) E ( G i d e a l ) E_{glob}(G)=\frac{E(G)}{E(G^{ideal})} Eglob(G)=E(Gideal)E(G)
3.27 Eulerian 欧拉图
3.28 Flows 流量
3.29 Graphical degree sequence 度序列
顶点的度的单调非递增序列。
3.30 Hierarchy 层次网络
3.31 Hybrid 混合
(k,l)-连接子图是对于每一对边都有至少 l l l条长度 ≤ k \le k ≤k的不相交的边。
3.32 Isolates 孤立节点
查找度数为0的节点。
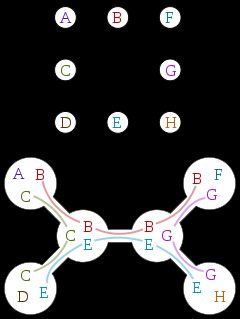
3.33 Isomorphism 同构
3.34 Link Analysis 链路分析
下面有PageRank算法。
3.35 Link Prediction
链路预测算法。
3.36 Lowest Common Ancestor 最近共同祖先
二分树中查找最近的共同祖先
3.37 Matching 匹配
不相连的边的组合
3.38 Minors 副图
如果无向图G能通过删除边和顶点、合并边得到H,则H是G的副图。
| H | G | 方法 |
|---|---|---|
 |
 |
 |
3.39 Maximal independent set 最大独立集
不相连的点的集合
3.40 Node Classification 节点分类
3.40.1 Harmonic Function
3.40.2 Local and Global Consistency 本地和全局一致性
3.41 Operators 运算
3.41.1 Complement 补图
3.41.2 Reverse 反向
将有向图中的边反向。
3.42 Planarity 平面图
| 平面图 | 非平面图 |
|---|---|
| 蝴蝶图 |
 完全图 完全图 |
3.43 Reciprocity 互惠性
互惠用于衡量有向网络中顶点相互连接的可能性。
Gallos在一些真实的社交网络中分析了互惠性。
3.44 Rich Club 富人聚集
Rich节点是极少数的有大量连接的结点。
3.45 Shortest Paths 最短路径
3.46 Similarity Measures 相似性衡量
3.47 Simple Paths 简单路径
3.48 Similarity Measures 相似性衡量
用于估计图的小世界效应的函数。
3.49 s metric S矩阵
s-metric = ∑ \sum ∑ deg(u)*deg(v) for 每一条边(u,v)
3.50 Sparsifiers
3.51 Structural holes
3.52 Swap 交换边
3.53 Tournament 锦标赛
锦标赛是完全无向图, 然后为每条边赋予任意方向, 变成有向图。
3.54 Traversal 遍历
3.54.1 深度优先搜索
获得前任、后继,进行点的遍历、节点的遍历
3.54.2 广度优先搜索
返回BFS树、前任、后继,对边进行遍历。
3.55 Tree 树
3.55.1 树的识别
返回图G是否是树、是否是森林等。
3.55.2 Branchings and Spanning Arborescences
Algorithms for finding optimum branchings and spanning arborescences. 寻找最佳分支和跨越树状的算法。
3.56 Triads 三元
3.57 Vitality 节点的活力
节点的紧密度活力。
紧密度活力是排除该节点时所有节点对的距离之和的变化。
3.58 Voronoi cells 沃罗诺伊图
把平面分割成区域
3.59 Wiener index 维纳指数
与化学特性有关。维纳指数=每一对连通的节点的最短路径之和。