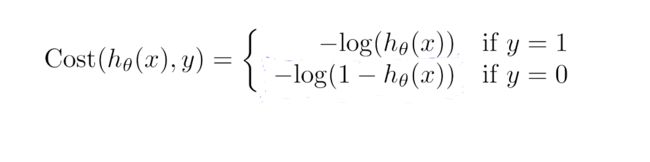coursera-斯坦福-机器学习-吴恩达-第3周笔记-逻辑回归
coursera-斯坦福-机器学习-吴恩达-第3周笔记-逻辑回归
文章目录
- coursera-斯坦福-机器学习-吴恩达-第3周笔记-逻辑回归
- 1.分类 和 模型表示
- 1.1分类的概念 Classification
- 1.2 分类模型表示
- 1.3 分类边界
- 2.逻辑回归模型 logistic regression
- 2.1 代价函数 cost func
- 2.2 梯度下降
- 2.3 高级优化方法(相对于梯度下降)
- 2.4 复习逻辑回归
- 3.多分类任务
- 4.过拟合overfitting
- 4.1 什么是过拟合
- 4.2 修改代价函数实现正则化
- 4.3 在线性回归中使用正则化
- 4.4 在逻辑回归中使用正则化
- 5.编程作业2
- 5.1 逻辑回归练习
- 5.1.1 可视化数据 Visualizing the data
- 5.1.2 实现
- 5.1.3 Learning parameters using fminunc
- 5.1.4 评估逻辑回归
- 5.2 正则化逻辑回归 Regularized logistic regression
- 5.1.1 可视化数据
- 5.1.2 特征映射Feature mapping
- 5.1.3 Cost function and gradient
- 5.1.4 画出决策边界Plotting the decision boundary
1.分类 和 模型表示
这一周对应PPT lecture6 逻辑回归
1.1分类的概念 Classification
先来谈谈二分类问题。课程中先给出了几个例子。
- 邮件是垃圾邮件还是非垃圾邮件;
- 网上交易是的欺骗性(Y or N);
- 肿瘤是恶性的还是良性的。
对于这些问题,我们可以通过输出值y ϵ {0, 1} 来表示。
注意:分类结果是离散值,这是分类的根本特点。
1.2 分类模型表示
通过上次的课程,我们可以想到利用假设函数y=hθ(x)来预测分类。
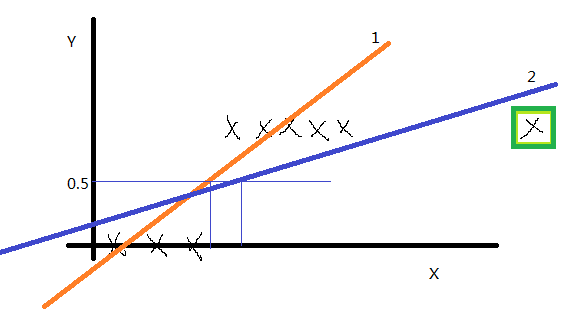
如果y的取值只有0和1,训练集画出来这这个样子(先没有绿框中的点),我们用线性回归得到1号直线,如果认为模拟直线的取值小于0.5时则预测值就为0,如果模拟直线的取值大于0.5时预测值就为1,感觉还不错。但是将绿框中的点加入后,线性回归得到的直线2,就显得不是很完美了。经过大量的实验证明,线性回归不适合这种训练集。那么怎么解决这个问题呢?
而且普通的hθ(x)函数存在函数值大于1和小于0的情况(没有意义),于是我们要构造特殊函数使0≤hθ(x)≤1。
我们提出来了一种新的回归模型:
y = h θ ( x ) = g ( θ T x ) y=h_\theta(x) = g(\theta^Tx) y=hθ(x)=g(θTx)
其中:
g ( z ) = 1 1 + e − z g(z) = \frac{1}{1 + e^{-z}} g(z)=1+e−z1
则
h θ ( x ) = 1 1 + e − θ T x h_\theta(x) = \frac{1}{1 + e^{-\theta^Tx}} hθ(x)=1+e−θTx1
g(z)这个函数称之为:logistic function 或者 sigmoid function
,其图像为:

1.3 分类边界
有了模型,怎么分类呢?
当y>0.5的时候,为正。此时由图像可知:
$h_\theta(x) \geq 0.5 $
θ T x ≥ 0 \theta^Tx\geq 0 θTx≥0
下面的图可以用来体会一下边界的含义
2.逻辑回归模型 logistic regression
2.1 代价函数 cost func
让我们先来看看线性回归中的代价函数 ,
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2 J(θ)=2m1∑i=1m(hθ(x(i))−y(i))2
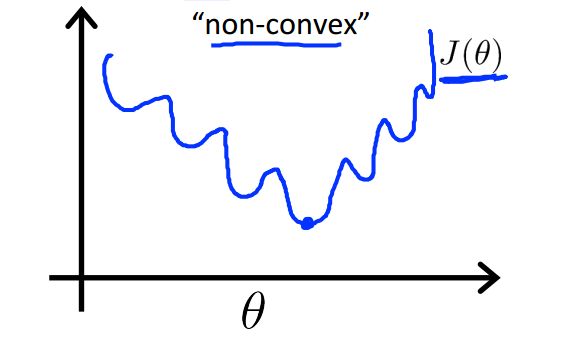
如果将其应用在逻辑回归中,由于假设函数hθ(x) 的非线性,代价函数会呈现以下形状。
图像呈现出非凸性,也就是说,如果我们运用梯度下降法,不能保证算法收敛到全局最小值。
对上面的式子进行简化,总结如下
J ( θ ) = 1 2 m ∑ i = 1 m C o s t ( h θ ( x ( i ) ) , y ( i ) ) J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}Cost(h_\theta(x^{(i)}), y^{(i)}) J(θ)=2m1i=1∑mCost(hθ(x(i)),y(i))
C o s t ( h θ ( x ( i ) ) , y ( i ) ) = − y ( i ) l o g ( h θ ( x ) ) − ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) Cost(h_\theta(x^{(i)}), y^{(i)}) = -y^{(i)}log(h_\theta(x)) - (1 - y^{(i)})log(1 - h_\theta(x^{(i)})) Cost(hθ(x(i)),y(i))=−y(i)log(hθ(x))−(1−y(i))log(1−hθ(x(i)))
即:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(\theta) = - \frac{1}{m} \displaystyle \sum_{i=1}^m [y^{(i)}\log (h_\theta (x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)}))] J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
他$的图像如下:
[外链图片转存失败(img-dzMKdJOI-1566960815283)(https://d3c33hcgiwev3.cloudfront.net/imageAssetProxy.v1/Q9sX8nnxEeamDApmnD43Fw_1cb67ecfac77b134606532f5caf98ee4_Logistic_regression_cost_function_positive_class.png?expiry=1511913600000&hmac=OTz6NTsejpcx9G03huJNlyQw6QPTq0RDuiefhb0SEUs)][外链图片转存失败(img-RCgJGXnc-1566960815284)(https://d3c33hcgiwev3.cloudfront.net/imageAssetProxy.v1/Ut7vvXnxEead-BJkoDOYOw_f719f2858d78dd66d80c5ec0d8e6b3fa_Logistic_regression_cost_function_negative_class.png?expiry=1511913600000&hmac=4ADldZaYgRx8HpjUgmirXmbZyHAZ7V5vdYEPJFlhV9E)]
如果我们的正确答案“y”是0,那么如果我们的假设函数也输出0,则成本函数将是0。如果我们的假设接近1,则成本函数将接近无穷大。
如果我们的正确答案“y”是1,那么如果我们的假设函数输出1,则成本函数将为0.如果我们的假设接近0,则成本函数将接近无穷大.
这种方式编写成本函数可以保证J(θ)对于逻辑回归是凸的。
2.2 梯度下降
请记住,梯度下降的一般形式是
Repeat{
θ j : = θ j − α ∂ ∂ θ j J ( θ ) \theta_j := \theta_j - \alpha \dfrac{\partial}{\partial \theta_j}J(\theta) θj:=θj−α∂θj∂J(θ)
}
我们可以使用微积分来计算微分部分以得到:
Repeat{
θ j : = θ j − α m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j := \theta_j - \frac{\alpha}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} θj:=θj−mαi=1∑m(hθ(x(i))−y(i))xj(i)
}
算法看上去和线性回归保持一致
2.3 高级优化方法(相对于梯度下降)
“共轭梯度Conjugate gradient”,“BFGS”和“L-BFGS”
是可以用来代替梯度下降来优化θ的更复杂,更快捷的方法。
对于梯度下降法我们可以在octive中使用如下高级函数
其中要定义代价函数costFunction:
f u n c t i o n [ j V a l , g r a d i e n t ] = c o s t F u n c t i o n ( t h e t a ) function [jVal, gradient] = costFunction(theta) function[jVal,gradient]=costFunction(theta)
2.4 复习逻辑回归
按照惯例,我们复习一下逻辑回归,写出三个维度的函数:
- 模型层面:逻辑回归模型
h θ ( x ) = 1 1 + e − θ T x h_\theta(x) = \frac{1}{1 + e^{-\theta^Tx}} hθ(x)=1+e−θTx1 - 代价函数:cost func
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(\theta) = - \frac{1}{m} \displaystyle \sum_{i=1}^m [y^{(i)}\log (h_\theta (x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)}))] J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
- 梯度下降
θ j : = θ j − α m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j := \theta_j - \frac{\alpha}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} θj:=θj−mαi=1∑m(hθ(x(i))−y(i))xj(i)
3.多分类任务
文中给出的多分类解决办法是,把K分类转换为K个2分类。例如:
[外链图片转存失败(img-N54ZJ7l7-1566960815288)(https://d3c33hcgiwev3.cloudfront.net/imageAssetProxy.v1/cqmPjanSEeawbAp5ByfpEg_299fcfbd527b6b5a7440825628339c54_Screenshot-2016-11-13-10.52.29.png?expiry=1511913600000&hmac=oODQb7xuCVv9WYVra6pXZokcv0OniEOiyN5Vmh_Ojss)]
训练每个类别的逻辑回归分类器hθ(x)来预测y的概率。
最后,选择最大化 max hθ(x)的类,
4.过拟合overfitting
这一章对应PPT lecture7 过拟合
4.1 什么是过拟合
考虑从x∈R预测y的问题。图片显示了将y 拟合到数据集的结果。
[外链图片转存失败(img-bhBUTu8U-1566960815289)(https://d3c33hcgiwev3.cloudfront.net/imageAssetProxy.v1/0cOOdKsMEeaCrQqTpeD5ng_2a806eb8d988461f716f4799915ab779_Screenshot-2016-11-15-00.23.30.png?expiry=1511913600000&hmac=bJgjHAo8SuQpms3nVRG2koNcYD7yDIM0aW7qlMRTtwY)]
左边是underfitting 也叫高偏差bias,中间是just right,右边是overfitting
overfitting通常是由一个复杂的函数造成的,这个函数会产生大量与数据无关的不必要的曲线和角度。
有两个主要的选择来解决过度拟合的问题:
1)减少特征的数量:
- 手动选择要保留的功能。
- 使用模型选择算法(在课程后面研究)。
2)正则化
- 保留所有的特征,但是减小参数θj的大小。
4.2 修改代价函数实现正则化
我们要消除θ3x3和θ4x4的影响。如果没有真正摆脱这些特征或改变我们假设的形式,我们可以修改我们的成本函数:
m i n θ 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + 1000 ⋅ θ 3 2 + 1000 ⋅ θ 4 2 min_\theta\ \dfrac{1}{2m}\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + 1000\cdot\theta_3^2 + 1000\cdot\theta_4^2 minθ 2m1i=1∑m(hθ(x(i))−y(i))2+1000⋅θ32+1000⋅θ42
最后我们增加了两个额外的术语来夸大θ3和θ4的成本。
现在,为了使成本函数接近零,我们将不得不将θ3和θ4的值减小到接近零。
这又会大大减少我们的假设函数中的θ3x3和θ4x4的值。
因此,我们看到新的假设(由粉红色曲线表示)看起来像一个二次函数,但是由于额外的小项θ3x3和θ4x4,所以更好地拟合数据。
[外链图片转存失败(img-WgAvktlZ-1566960815290)(https://d3c33hcgiwev3.cloudfront.net/imageAssetProxy.v1/j0X9h6tUEeawbAp5ByfpEg_ea3e85af4056c56fa704547770da65a6_Screenshot-2016-11-15-08.53.32.png?expiry=1511913600000&hmac=7k3qwY698XAeJFXmQnQZ7CImsAFoWzTeMgCnIaaMM7E)]
所以, 在代价函数后面加上一些乘法系数,可以“捋平”图像的弯曲,完成泛化。
但是,在实际情况中,我们不知道具体惩罚哪个θ,所以就整体惩罚,把每个弯平一平。也就是修改代价函数为:
m i n θ 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 min_\theta\ \dfrac{1}{2m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda\ \sum_{j=1}^n \theta_j^2 minθ 2m1 i=1∑m(hθ(x(i))−y(i))2+λ j=1∑nθj2
其中λ是正则化参数 regularization parameter。它决定了我们θ参数的成本膨胀了多少。
如果选择的lambda太大,可能会使功能过于平滑,under fitting。
因此,如果λ= 0或太小会发生泛化失败,overfitting
4.3 在线性回归中使用正则化
我们可以将正则化应用于线性回归和逻辑回归。(因为就学了这俩)
我们将首先处理线性回归。 一共有两种方法,梯度下降和正规方程
-
梯度下降
我们将修改我们的梯度下降函数,从其他参数中分离出θ0,因为我们不想惩罚θ0。
Repeat {}
θ j : = θ j − α [ ( 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ) + λ m θ j ] \theta_j := \theta_j - \alpha\ \left[ \left( \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} \right) + \frac{\lambda}{m}\theta_j \right] θj:=θj−α [(m1 i=1∑m(hθ(x(i))−y(i))xj(i))+mλθj]
通过一些操作,我们的更新规则也可以表示为:
θ j : = θ j ( 1 − α λ m ) − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j := \theta_j(1 - \alpha\frac{\lambda}{m}) - \alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} θj:=θj(1−αmλ)−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
上面的等式中的第一项1-α λ/m将总是小于1.直觉上你可以看到它在每次更新时减少θj的值一定量 -
正规方程
现在让我们使用非迭代法线方程的替代方法来进行正则化。
θ = ( X T X + λ ⋅ L ) − 1 X T y \theta = \left( X^TX + \lambda \cdot L \right)^{-1} X^Ty θ=(XTX+λ⋅L)−1XTy
L是一个矩阵,左上角为0,下角为1,其他地方为0。
它应该有维度(n 1)×(n 1)。
直观地说,这是单位矩阵(尽管我们不包括x0),乘以单个实数λ。
回想一下,如果m 4.4 在逻辑回归中使用正则化
我们可以用类似的方式调整逻辑回归,就像我们调整线性回归一样。
因此,我们可以避免过度配合。
下图显示了粉红线所显示的正则化函数如何比蓝线所表示的非正则化函数更不可能过配:
[外链图片转存失败(img-qiINT8Yr-1566960815292)(https://d3c33hcgiwev3.cloudfront.net/imageAssetProxy.v1/Od9mobDaEeaCrQqTpeD5ng_4f5e9c71d1aa285c1152ed4262f019c1_Screenshot-2016-11-22-09.31.21.png?expiry=1511913600000&hmac=VObCxzbuzkNtYu-rssJQU5P4tCB91HaP8NlIVhb-0Mk)]
回想一下,逻辑回归的成本函数是:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(\theta) = - \frac{1}{m} \sum_{i=1}^m \large[ y^{(i)}\ \log (h_\theta (x^{(i)})) + (1 - y^{(i)})\ \log (1 - h_\theta(x^{(i)})) \large] J(θ)=−m1i=1∑m[y(i) log(hθ(x(i)))+(1−y(i)) log(1−hθ(x(i)))]
我们可以通过在最后添加一个术语来规范这个等式:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta) = - \frac{1}{m} \sum_{i=1}^m \large[ y^{(i)}\ \log (h_\theta (x^{(i)})) + (1 - y^{(i)})\ \log (1 - h_\theta(x^{(i)}))\large] + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2 J(θ)=−m1i=1∑m[y(i) log(hθ(x(i)))+(1−y(i)) log(1−hθ(x(i)))]+2mλj=1∑nθj2
第二个和Σnj=1θ2j意味着明确排除偏差项θ0。即θ矢量从0到n(保持n 1个值,θ0到θn)被索引,并且该和明确跳过θ0,从1跳到n,跳过0.因此,当计算等式时,我们应该连续更新两个以下等式:
[外链图片转存失败(img-LjfSb9cI-1566960815293)(https://d3c33hcgiwev3.cloudfront.net/imageAssetProxy.v1/dfHLC70SEea4MxKdJPaTxA_306de28804a7467f7d84da0fe3ee9c7b_Screen-Shot-2016-12-07-at-10.49.02-PM.png?expiry=1511913600000&hmac=6GJOdiQ3K-7Vajfumk1pZaPd1pjqINq84CkEYrVtem0)]
5.编程作业2
首先下载作业:
Download the programming assignment here.
此ZIP文件包含PDF和启动器代码中的说明。
首先是PDF简介:
在本练习中,您将执行逻辑回归并将其应用于两个不同的数据集。 在开始编程练习之前,我们强烈建议您观看视频讲座并完成相关主题的复习问题。
要开始练习,您需要下载初学者代码并将其内容解压到您希望完成练习的目录。 如果需要,在开始本练习之前,使用Octave / MATLAB中的cd命令切换到此目录。
各个文件的作用:
ex2.m - Octave / MATLAB脚本,指导您完成练习
ex2 reg.m - 练习后面部分的Octave / MATLAB脚本
ex2data1.txt - 练习的前半部分的训练集
ex2data2.txt - 练习后半部分的训练集
submit.m - 提交您的解决方案到我们的服务器的提交脚本
mapFeature.m - 生成多项式特征的函数
plotDecisionBoundary.m - 绘制分类器决策边界的函数
在整个练习中,您将使用脚本ex2.m和ex2 reg.m. 这些脚本为问题设置数据集,并调用您将要编写的函数。 你不需要修改其中的任何一个。 您只需按照本作业中的说明修改其他文件中的功能。
5.1 逻辑回归练习
在这部分的练习中,你将建立一个逻辑回归模型来预测一个学生是否被录取进大学。
假设你是大学部门的管理者,你想根据两次考试的结果来确定每个申请者的录取机会。 您可以从以前的申请人获得历史数据,您可以将其用作逻辑回归的训练集。 对于每个培训的例子,你有两个考试的申请者的分数和录取决定。
你的任务是建立一个分类模型,根据这两个考试的分数来估计申请者的录取概率。
这个大纲和ex2.m中的框架代码将指导你完成这个练习。
5.1.1 可视化数据 Visualizing the data
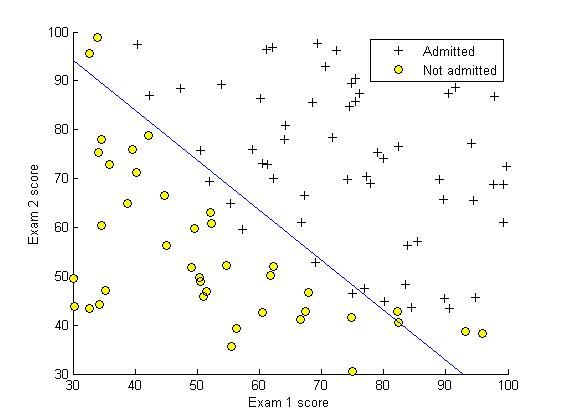
在开始实施任何学习算法之前,如果可能的话,最好将数据可视化。 在ex2.m的第一部分,代码将加载数据并通过调用函数plotData将其显示在二维图上。
您现在将在plotData中完成代码,使其显示如图1所示的图形,其中轴是两个考试分数,正面和负面的示例显示为不同的标记。
我们打开文件plotData.m编辑,在其中加入:
% Find Indices of Positive and Negative Examples
pos = find(y==1); neg = find(y == 0);
% Plot Examples
plot(X(pos, 1), X(pos, 2), 'k+','LineWidth', 2, ...
'MarkerSize', 7);
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'y', ...
'MarkerSize', 7);
5.1.2 实现
- 实现 sigmoid
打开 sigmoid.m编辑加入一行即可:
g = 1./(1+exp(-z));
- 实现Cost function and gradient
打开 costFunction.m编辑加入:
J = 1/m*(-y'*log(sigmoid(X*theta)) - (1-y)'*(log(1-sigmoid(X*theta))));
grad = 1/m * X'*(sigmoid(X*theta) - y);
5.1.3 Learning parameters using fminunc
在前面的作业中,通过执行渐变下降,找到了线性回归模型的最佳参数。 您编写了一个成本函数并计算了它的梯度,然后相应地进行了梯度下降步骤。
这一次,你将使用一个名为fminunc的Octave / MATLAB内置函数。
Octave / MATLAB的fminunc是一个优化求解器,可以找到一个无约束2函数的最小值。 对于逻辑回归,您想用参数θ来优化成本函数J(θ)。
请注意,通过使用fminunc,您不必自己编写任何循环,也可以像设置渐变下降一样设置学习速度。 这一切都是由fminunc完成的:你只需要提供一个计算成本和梯度的函数.(前面已经提供)
5.1.4 评估逻辑回归
学习完参数后,您可以使用该模型来预测某个特定的学生是否被录取。 对于考试1分为45分和考试2分为85分的学生,您应该期望看到0.776的录取概率。
评估我们发现的参数质量的另一种方法是看看学习模型在我们的训练集上的预测程度。 在这一部分中,您的任务是完成predict.m中的代码。 给定数据集和学习参数矢量θ,预测函数将产生“1”或“0”预测。
完成predict.m中的代码之后,ex2.m脚本将通过计算正确示例的百分比来报告分类器的训练准确性。
打开 predict.m编辑加入:
p = sigmoid(X * theta)>=0.5;
5.2 正则化逻辑回归 Regularized logistic regression
在这部分的练习中,您将执行正则化的逻辑回归来预测制造工厂的微芯片是否通过了质量保证(QA)。 在QA期间,每个微芯片都经过各种测试以确保其正常工作。
假设你是工厂的产品经理,你在两个不同的测试中有一些微芯片的测试结果。 从这两个测试,你想确定是否应该接受或拒绝芯片。 为了帮助您做出决定,您可以在过去的微芯片上获得测试结果的数据集,从中可以建立逻辑回归模型。
您将使用另一个脚本ex2 reg.m来完成这部分练习。
5.1.1 可视化数据
图显示我们的数据集不能通过绘图的直线分成正面和负面的例子。 因此,logistic回归的直接应用在这个数据集上表现不好,因为逻辑回归只能找到一个线性的决策边界。
5.1.2 特征映射Feature mapping
更好地拟合数据的一种方法是从每个数据点创建更多的特征。 在提供的函数mapFeature.m中,我们将把特征映射到x 1和x 2的所有多项式到6次幂。
作为这种映射的结果,我们的两个特征(两个QA测试中的分数)的矢量已被变换成28维矢量。 在这个高维特征向量上训练的逻辑回归分类器将具有更复杂的决策边界,并且在我们的二维图中绘制时将呈现非线性。
虽然特征映射允许我们构建更具表现力的分类器,但它也更易于过度拟合。 在接下来的练习中,您将实施规则化的逻辑回归以适应数据,同时也要了解正规化如何帮助解决过度拟合问题。
5.1.3 Cost function and gradient
现在您将执行代码来计算正则化逻辑回归的成本函数和梯度。 完成costFunctionReg.m中的代码以返回成本和渐变
就是在原来的代价函数的基础上加入正则项:
在costFunctionReg.m中加:
J = 1/m * (-y' * log(sigmoid(X*theta)) - (1 - y') * log(1 - sigmoid(X * theta))) + lambda/2/m*sum(theta(2:end).^2);
grad(1,:) = 1/m * (X(:, 1)' * (sigmoid(X*theta) - y));
grad(2:size(theta), :) = 1/m * (X(:, 2:size(theta))' * (sigmoid(X*theta) - y))...
+ lambda/m*theta(2:size(theta), :);
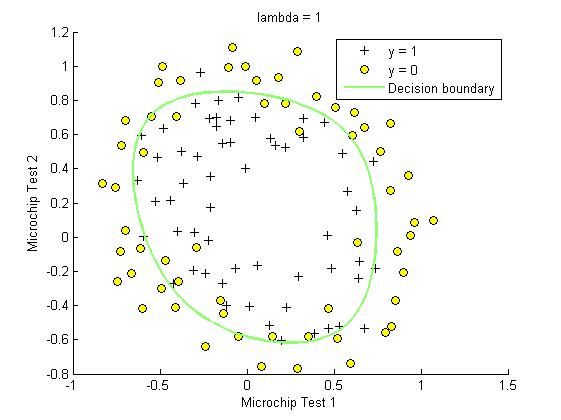
5.1.4 画出决策边界Plotting the decision boundary
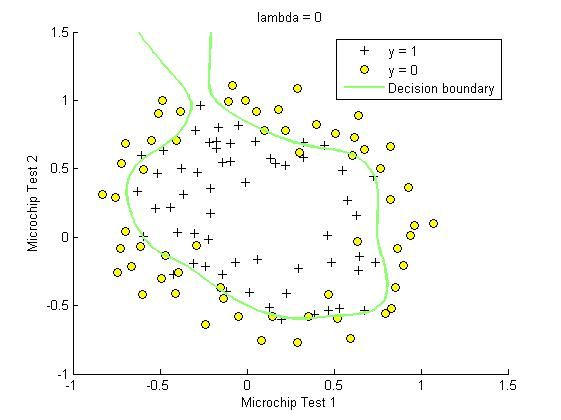
为了帮助您可视化由此分类器学习的模型,我们提供了plotDecisionBoundary.m函数,绘制分隔正例和负例的(非线性)决策边界。 在plotDecisionBoundary.m中,我们通过在均匀间隔的网格上计算分类器的预测来绘制非线性决策边界,然后画出预测从y = 0变化到y = 1的等高线图。
在学习参数θ之后,ex reg.m中的下一步将绘制类似于图4的决策边界。
精确度89%左右