POJ 1542 Atlantis（线段树 面积并+离散化）

题目链接： http://acm.hdu.edu.cn/showproblem.php?pid=1542
参考网址：http://blog.csdn.net/sunmenggmail/article/details/7984589

Problem Description

There are several ancient Greek texts that contain descriptions of the fabled island Atlantis. Some of these texts even include maps of parts of the island. But unfortunately, these maps describe different regions of Atlantis. Your friend Bill has to know the total area for which maps exist. You (unwisely) volunteered to write a program that calculates this quantity.

 

Input

The input file consists of several test cases. Each test case starts with a line containing a single integer n (1<=n<=100) of available maps. The n following lines describe one map each. Each of these lines contains four numbers x1;y1;x2;y2 (0<=x1
The input file is terminated by a line containing a single 0. Don’t process it.

 

Output

For each test case, your program should output one section. The first line of each section must be “Test case #k”, where k is the number of the test case (starting with 1). The second one must be “Total explored area: a”, where a is the total explored area (i.e. the area of the union of all rectangles in this test case), printed exact to two digits to the right of the decimal point.

Output a blank line after each test case.

 

Sample Input

2 10 10 20 20 15 15 25 25.5 0

 

Sample Output

Test case #1 Total explored area: 180.00

 

Source

Mid-Central European Regional Contest 2000

 

Recommend

linle   |   We have carefully selected several similar problems for you:   1828  1255  1698  1540  1754

题意：题意很简单，就是求矩形面积的并

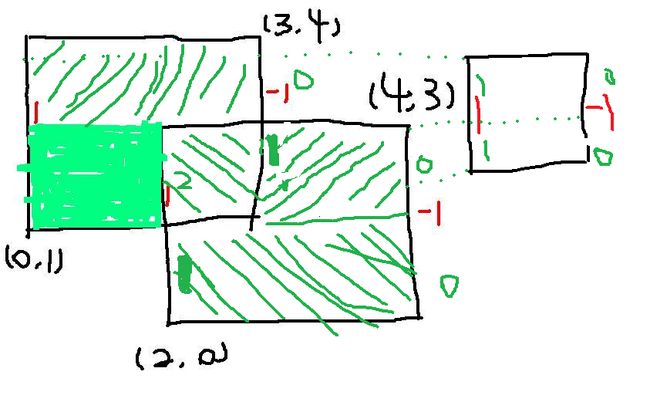
给定一个矩形的左下角坐标和右上角坐标分别为:(x1,y1)、(x2,y2)，对这样的一个矩形，我们构造两条线段，一条定位在x1，它在y坐标的区间是[y1,y2]，并且给定一个cover域值为1；另一条线段定位在x2，区间一样是[y1,y2]，给定它一个cover值为-1。根据这样的方法对每个矩形都构造两个线段，最后将所有的线段根据所定位的x从左到右进行排序。

上图中，红色的字体表示的是该线段的左右标志，绿色字体为当前更新到当前线段的cover值。刚刚开始的时候，线段树上的cover值都为0，但第一根线段(x==0)插入线段树的之后，我们将线段树上的cover加上该线段的cover，那么，此时线段树上被该线段覆盖的位置上的cover的值就为1，下次再插入第二根线段（x==1）此时发现该线段所覆盖的区间内，有一部分线段树的cover为0，另有一部分为1，仔细观察，但插入第二个线段的时候，如果线段树上cover已经为1的那些区间，和现在要插入的第二根线段之间，是不是构成了并面积？还不明白？看下图，绿色部分即为插入第二根线段后得到的并面积

#include 
#include 
#include 
using namespace std;
const int maxn=110;
struct LINE
{
    double  x, y_down, y_up;
    int  flag;
    bool operator<(const LINE &a)const  ///按照x从小到大的顺序排序
    {
        return  x>1;
       build(2*i, l, mid);
       build(2*i+1, mid, r);
}

double insert(int i, double x, double l, double r, int flag) //flag表示为左边还是右边
{
    if ( r<=tree[i].y_down || l>=tree[i].y_up )   return 0;
    if (tree[i].flag) /// 叶子节点
    {
        if (tree[i].cover > 0) /// 该区域的面积存在，且未经计算
        {
             double temp_x = tree[i].x;
             double ans=( x-temp_x )*(tree[i].y_up - tree[i].y_down);
             tree[i].cover += flag;
             tree[i].x = x;   //定位上一次的x
             return ans;
        }
        else  ///虽然是叶子节点，但是需要更新当前的线段覆盖标记
        {
            tree[i].cover += flag;
            tree[i].x = x;  ///更新最新x
            return 0;
        }
    }
    return insert(2*i, x, l, r, flag)+insert(2*i+1, x, l, r, flag); ///不是叶子节点就往下递归
}

int main( )
{
   // freopen("d:\\in.txt","r",stdin);
    int  Case=0,n,index;
    double  x1, y1, x2, y2;
    while(~scanf("%d",&n) && n)
    {
        index = 1;
        for (int i=1; i<=n; i++)
        {
            scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
            y[index] = y1;
            line[index].x = x1;
            line[index].y_down = y1;
            line[index].y_up = y2;
            line[index++].flag = 1; //1表示左边

            y[index] = y2;
            line[index].x = x2;
            line[index].y_down = y1;
            line[index].y_up = y2;
            line[index++].flag = -1; //-1表示右边
        }
        sort(&y[1], &y[index]); //把所有的纵坐标按从小到大排序,把1写成了0，WA一次
        sort(&line[1], &line[index]);
        build(1, 1, index-1);
        double ans=0;
        for (int i=1;i

开始感觉和POJ 2528应该是一样的啊，为什么没有去重啊，于是写一个去重的，果断AC，之后想为什么？其实也很简单，因为在这里的是通过ans=( x-temp_x )*(tree[i].y_up - tree[i].y_down)这个公式求面积的，并且在Build的时候是排过序的，所以两个相邻的也就是叶子节点的(tree[i].y_up - tree[i].y_down)如果有重点就为0了，这样该段算出来的面积也就是0了，没有影响，但是感觉还是先去重之后比较清晰。

#include 
#include 
#include 
using namespace std;
const int maxn=110;
struct LINE
{
    double  x, y_down, y_up;
    int  flag; ///表示一个矩形的左边还是右边
    bool operator<(const LINE &a)const  ///按照x从小到大的顺序排序
    {
        return  x>1;
   build(2*i, l, mid);
   build(2*i+1, mid, r);
}

double insert(int i, double x, double l, double r, int flag) //flag表示为左边还是右边
{         ///父节点  当前线段的x值 y_Down   y_Up
    if ( r<=tree[i].y_down || l>=tree[i].y_up )   return 0;
    if (tree[i].flag) /// 叶子节点
    {
        double ans = 0;
        if (tree[i].cover > 0) /// 该区域的面积存在，且未经计算
        {
             double temp_x = tree[i].x;
             ans=( x-temp_x )*(tree[i].y_up - tree[i].y_down);
        }
         ///更新该线段最新的x坐标和被覆盖情况
         tree[i].cover += flag;
         tree[i].x = x;   //定位上一次的x

         return ans;
    }
    return insert(i<<1, x, l, r, flag)+insert(i<<1|1, x, l, r, flag); ///不是叶子节点就往下递归
}

int main( )
{
   // freopen("d:\\in.txt","r",stdin);
    int  Case=0,n,index;
    double  x1, y1, x2, y2;
    while(~scanf("%d",&n) && n)
    {
        index = 1;
        for (int i=1; i<=n; i++)
        {
            scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
            y[index] = y1;
            line[index].x = x1;
            line[index].y_down = y1;
            line[index].y_up = y2;
            line[index].flag = 1; //1表示左边
            index++;

            y[index] = y2;
            line[index].x = x2;
            line[index].y_down = y1;
            line[index].y_up = y2;
            line[index].flag = -1; //-1表示右边
            index++;
        }
        sort(&y[1], &y[index]); //把所有的纵坐标按从小到大排序,把1写成了0，WA一次
        sort(&line[1], &line[index]);

        int nCount=unique(&y[1],&y[index])-(&y[1]);
        build(1, 1, nCount);

        double ans=0;
        for (int i=1;i