【计算机编程思想系列 1】递归(Recursion)
To iterate is human, to recurse, divine.
人理解迭代,神理解递归。
递归(Recursion algorithm),在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。
递归式方法可以被用于解决很多的计算机科学问题,因此它是计算机科学中十分重要的一个概念。绝大多数编程语言支持函数的自调用,在这些语言中函数可以通过调用自身来进行递归。
计算理论可以证明递归的作用可以完全取代循环,因此在很多函数编程语言(如Scheme)中习惯用递归来实现循环。
假设我们用递归来算阶乘 f(n)
f (n) -> n == 1 ? 1 : n * f(n-1)
f 里面用到了 f,怎么理解呢?很简单,把式子展开即可:
f(6)
=> 6 * f(5)
=> 6 * (5 * f(4))
=> 6 * (5 * (4 * f(3)))
=> 6 * (5 * (4 * (3 * f(2))))
=> 6 * (5 * (4 * (3 * (2 * f(1)))))
=> 6 * (5 * (4 * (3 * (2 * 1))))
=> 6 * (5 * (4 * (3 * 2)))
=> 6 * (5 * (4 * 6))
=> 6 * (5 * 24)
=> 6 * 120
=> 720
代码示例
/**
* @author: Jack
* 2020-01-11 02:35
*/
class NavTree : NavVisitable {
var deptNo = ""
var deptName = ""
var hasPermission = false
var leaf = false
var children : MutableList = mutableListOf()
constructor(deptNo: String, deptName: String, hasPermission: Boolean, leaf: Boolean) {
this.deptNo = deptNo
this.deptName = deptName
this.hasPermission = hasPermission
this.leaf = leaf
}
/**
* 接受访问:递归遍历
*/
override fun accept(visitor: NavVisitor) {
// 访问当前节点
visitor.visitTree(this)
if (children != null) {
// 访问所有孩子节点
for (child in this.children!!) {
val childVisitor = visitor.visitTree(child)
child.accept(childVisitor)
}
}
}
/**
* 构建孩子节点列表
*/
fun children(node: NavTree): NavTree {
if (children != null) {
for (child in children) {
if (child.deptNo == node.deptNo) {
return child
}
}
children.add(node)
}
return node
}
override fun toString(): String {
return "NavTree(deptNo='$deptNo', deptName='$deptName', hasPermission=$hasPermission, leaf=$leaf, children=$children)"
}
}
递归思想
interface TreeVisitor {
/**
* 访问函数
*
* @param t 访问对象(树节点)
*/
void visit(ItemVO t);
}
/**
* 访问者模式,递归遍历树节点
*
* @param t 树节点
* @param visitor 访问者
*/
private static void visitTree(ItemVO t, TreeVisitor visitor) {
visitor.visit(t);
if (null != t.children) {
for (ItemVO child : t.children) {
visitTree(child, visitor);
}
}
}
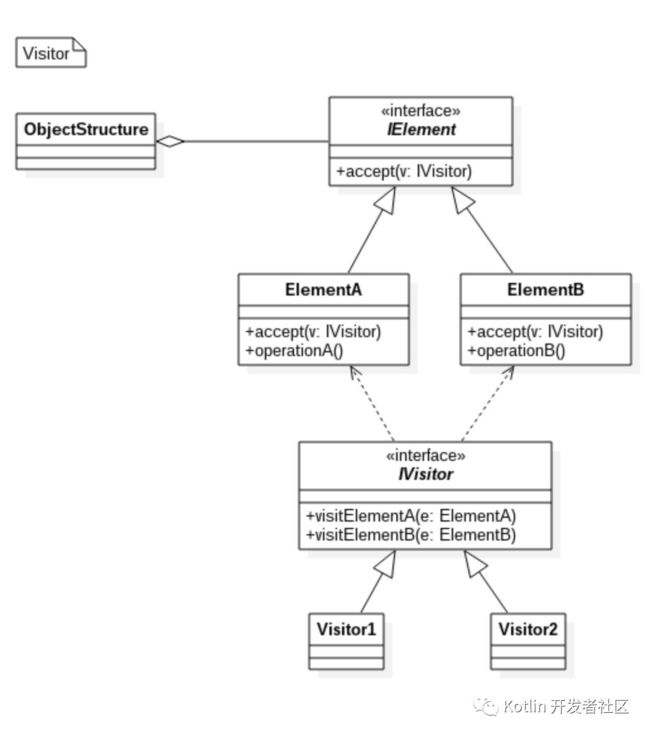
访问者设计模式
在访问者模式(Visitor Pattern)中,我们使用了一个访问者类,它改变了元素类的执行算法。通过这种方式,元素的执行算法可以随着访问者改变而改变。这种类型的设计模式属于行为型模式。根据模式,元素对象已接受访问者对象,这样访问者对象就可以处理元素对象上的操作。
介绍
意图:主要将数据结构与数据操作分离。
主要解决:稳定的数据结构和易变的操作耦合问题。
何时使用:需要对一个对象结构中的对象进行很多不同的并且不相关的操作,而需要避免让这些操作"污染"这些对象的类,使用访问者模式将这些封装到类中。
如何解决:在被访问的类里面加一个对外提供接待访问者的接口。
关键代码:在数据基础类里面有一个方法接受访问者,将自身引用传入访问者。
应用实例:您在朋友家做客,您是访问者,朋友接受您的访问,您通过朋友的描述,然后对朋友的描述做出一个判断,这就是访问者模式。
优点: 1、符合单一职责原则。2、优秀的扩展性。3、灵活性。
缺点: 1、具体元素对访问者公布细节,违反了迪米特原则。2、具体元素变更比较困难。3、违反了依赖倒置原则,依赖了具体类,没有依赖抽象。
使用场景: 1、对象结构中对象对应的类很少改变,但经常需要在此对象结构上定义新的操作。2、需要对一个对象结构中的对象进行很多不同的并且不相关的操作,而需要避免让这些操作"污染"这些对象的类,也不希望在增加新操作时修改这些类。
注意事项:访问者可以对功能进行统一,可以做报表、UI、拦截器与过滤器。
在数理逻辑和计算机科学中,递归函数或μ-递归函数是一类从自然数到自然数的函数,它是在某种直觉意义上是"可计算的" 。事实上,在可计算性理论中证明了递归函数精确的是图灵机的可计算函数。递归函数有关于原始递归函数,并且它们的归纳定义(见下)建造在原始递归函数之上。但是,不是所有递归函数都是原始递归函数 — 最著名的这种函数是阿克曼函数。
其他等价的函数类是λ-递归函数和马尔可夫算法可计算的函数。
递归求斐波那契数列
递归计算阶乘
Kotlin 开发者社区
国内第一Kotlin 开发者社区公众号,主要分享、交流 Kotlin 编程语言、Spring Boot、Android、React.js/Node.js、函数式编程、编程思想等相关主题。
越是喧嚣的世界,越需要宁静的思考。