K-means聚类算法的三种改进(K-means++,ISODATA,Kernel K-means)介绍与对比

  一、概述

      在本篇文章中将对四种聚类算法(K-means,K-means++,ISODATA和Kernel K-means)进行详细介绍，并利用数据集来真实地反映这四种算法之间的区别。

      首先需要明确的是上述四种算法都属于"硬聚类”算法，即数据集中每一个样本都是被100%确定得分到某一个类别中。与之相对的"软聚类”可以理解为每个样本是以一定的概率被分到某一个类别中。

      先简要阐述下上述四种算法之间的关系，已经了解过经典K-means算法的读者应该会有所体会。没有了解过K-means的读者可以先看下面的经典K-means算法介绍再回来看这部分。

     (1) K-means与K-means++：原始K-means算法最开始随机选取数据集中K个点作为聚类中心，而K-means++按照如下的思想选取K个聚类中心：假设已经选取了n个初始聚类中心(0

      (2) K-means与ISODATA：ISODATA的全称是迭代自组织数据分析法。在K-means中，K的值需要预先人为地确定，并且在整个算法过程中无法更改。而当遇到高维度、海量的数据集时，人们往往很难准确地估计出K的大小。ISODATA就是针对这个问题进行了改进，它的思想也很直观：当属于某个类别的样本数过少时把这个类别去除，当属于某个类别的样本数过多、分散程度较大时把这个类别分为两个子类别。

      (3) K-means与Kernel K-means：传统K-means采用欧式距离进行样本间的相似度度量，显然并不是所有的数据集都适用于这种度量方式。参照支持向量机中核函数的思想，将所有样本映射到另外一个特征空间中再进行聚类，就有可能改善聚类效果。本文不对Kernel K-means进行详细介绍。

      可以看到，上述三种针对K-means的改进分别是从不同的角度出发的，因此都非常具有代表意义。目前应用广泛的应该还是K-means++算法（例如2016年底的NIPS上也有针对K-means++的改进，感兴趣的读者可以进一步学习）。

 

二、经典K-means算法

    算法描述如下，非常清晰易懂。经典K-means算法应该是每个无监督学习教程开头都会讲的内容，故不再多费口舌说一遍了。

图1. 经典K-means算法

 

      值得一提的是关于聚类中心数目（K值）的选取，的确存在一种可行的方法，叫做Elbow Method：通过绘制K-means代价函数与聚类数目K的关系图，选取直线拐点处的K值作为最佳的聚类中心数目。但在这边不做过多的介绍，因为上述方法中的拐点在实际情况中是很少出现的。比较提倡的做法还是从实际问题出发，人工指定比较合理的K值，通过多次随机初始化聚类中心选取比较满意的结果。

 

三、K-means++算法

      2007年由D. Arthur等人提出的K-means++针对图1中的第一步做了改进。可以直观地将这改进理解成这K个初始聚类中心相互之间应该分得越开越好。整个算法的描述如下图所示：

    图2. K-means++算法

      下面结合一个简单的例子说明K-means++是如何选取初始聚类中心的。数据集中共有8个样本，分布以及对应序号如下图所示：

图3. K-means++示例

      假设经过图2的步骤一后6号点被选择为第一个初始聚类中心，那在进行步骤二时每个样本的D(x)和被选择为第二个聚类中心的概率如下表所示：

    其中的P(x)就是每个样本被选为下一个聚类中心的概率。最后一行的Sum是概率P(x)的累加和，用于轮盘法选择出第二个聚类中心。方法是随机产生出一个0~1之间的随机数，判断它属于哪个区间，那么该区间对应的序号就是被选择出来的第二个聚类中心了。例如1号点的区间为[0,0.2)，2号点的区间为[0.2, 0.525)。

      从上表可以直观的看到第二个初始聚类中心是1号，2号，3号，4号中的一个的概率为0.9。而这4个点正好是离第一个初始聚类中心6号点较远的四个点。这也验证了K-means的改进思想：即离当前已有聚类中心较远的点有更大的概率被选为下一个聚类中心。可以看到，该例的K值取2是比较合适的。当K值大于2时，每个样本会有多个距离，需要取最小的那个距离作为D(x)。

 

四、ISODATA算法

     放在最后也是最复杂的就是ISODATA算法。正如之前所述，K-means和K-means++的聚类中心数K是固定不变的。而ISODATA算法在运行过程中能够根据各个类别的实际情况进行两种操作来调整聚类中心数K：(1)分裂操作，对应着增加聚类中心数；(2)合并操作，对应着减少聚类中心数。

    下面首先给出ISODATA算法的输入（输入的数据和迭代次数不再单独介绍）：

      [1] 预期的聚类中心数目Ko：虽然在ISODATA运行过程中聚类中心数目是可变的，但还是需要由用户指定一个参考标准。事实上，该算法的聚类中心数目变动范围也由Ko决定。具体地，最终输出的聚类中心数目范围是 [Ko/2, 2Ko]。

      [2] 每个类所要求的最少样本数目Nmin：用于判断当某个类别所包含样本分散程度较大时是否可以进行分裂操作。如果分裂后会导致某个子类别所包含样本数目小于Nmin，就不会对该类别进行分裂操作。

      [3] 最大方差Sigma：用于衡量某个类别中样本的分散程度。当样本的分散程度超过这个值时，则有可能进行分裂操作（注意同时需要满足[2]中所述的条件）。

      [4] 两个类别对应聚类中心之间所允许最小距离dmin：如果两个类别靠得非常近（即这两个类别对应聚类中心之间的距离非常小），则需要对这两个类别进行合并操作。是否进行合并的阈值就是由dmin决定。

      相信很多人看完上述输入的介绍后对ISODATA算法的流程已经有所猜测了。的确，ISODATA算法的原理非常直观，不过由于它和其他两个方法相比需要额外指定较多的参数，并且某些参数同样很难准确指定出一个较合理的值，因此ISODATA算法在实际过程中并没有K-means++受欢迎。

      首先给出ISODATA算法主体部分的描述，如下图所示：

图4. ISODATA算法的主体部分

     上面描述中没有说明清楚的是第5步中的分裂操作和第6步中的合并操作。下面首先介绍合并操作：

图5. ISODATA算法的合并操作

     最后是ISODATA算法中的分裂操作。

图6. ISODATA算法的分裂操作

      最后，针对ISODATA算法总结一下：该算法能够在聚类过程中根据各个类所包含样本的实际情况动态调整聚类中心的数目。如果某个类中样本分散程度较大（通过方差进行衡量）并且样本数量较大，则对其进行分裂操作；如果某两个类别靠得比较近（通过聚类中心的距离衡量），则对它们进行合并操作。

       可能没有表述清楚的地方是ISODATA-分裂操作的第1步和第2步。同样地以图三所示数据集为例，假设最初1，2，3，4，5，6，8号被分到了同一个类中，执行第1步和第2步结果如下所示：

      而在正确分类情况下（即1，2，3，4为一类；5，6，7，8为一类），方差为0.33。因此，目前的方差远大于理想的方差，ISODATA算法就很有可能对其进行分裂操作。

 

五、聚类算法源代码

      我已经将上述三种算法整合成一个Matlab函数Clustering.m。读者可以直接使用该函数对数据集进行聚类。由于代码比较长，而且代码插件还不怎么会用，就不在文中介绍了。需要使用的读者可以点击下面的链接下载使用（欢迎Star和Fork，之后会不定期补充新的算法和优化的）：

https://github.com/AaronX121/Unsupervised-Learning-Clustering

     使用方式非常简单，目前支持三种形式的输入，分别对应着上面的三种算法：

     [centroid, result] = Clustering(data, ‘kmeans’, k , iteration);

     [centroid, result] = Clustering(data, ‘kmeans++’, k , iteration);

     [centroid, result] =

   Clustering(data, ‘isodata’, desired_k , iteration, minimum_n, maximum_variance, minimum_d);

      其中的输入data是一个矩阵，每一行代表数据集中的一个样本。其他输入的意义与上面的算法描述中一一对应。输出的centroid是聚类中心的位置，result是每个样本所对应的类别索引。

 

六、数据集测试

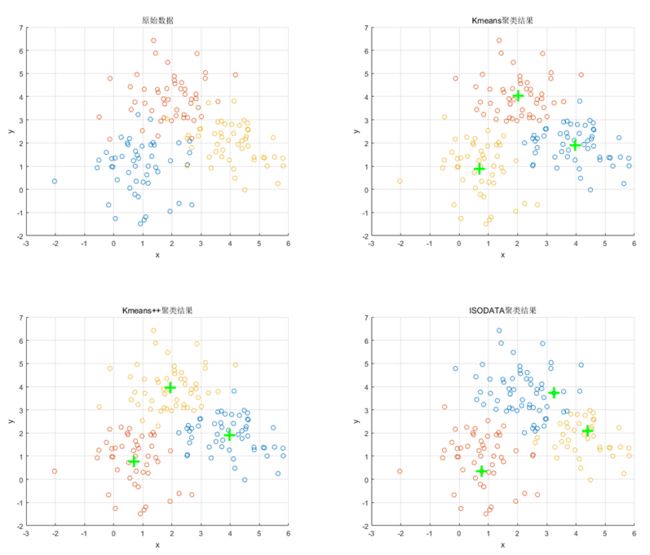
      最后以一个简单的满足二维高斯分布的数据集为例，展示上述三种算法的聚类结果，如下图所示。

图7. 一个简单数据集上三种算法的聚类效果（绿色加号代表聚类中心位置）

转载于:https://www.cnblogs.com/yixuan-xu/p/6272208.html