为什么80%的码农都做不了架构师?>>> ![]()
进度类计算
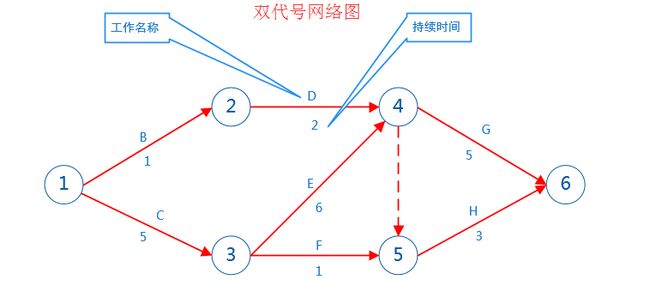
项目进度网络图
----展示项目各计划活动、持续时间、逻辑关系的图形
双代号网络图(箭线型)
----用一个箭线表示一项活动,活动名称写在箭线上,箭线同时表示活动间逻辑关系。
绘图规则
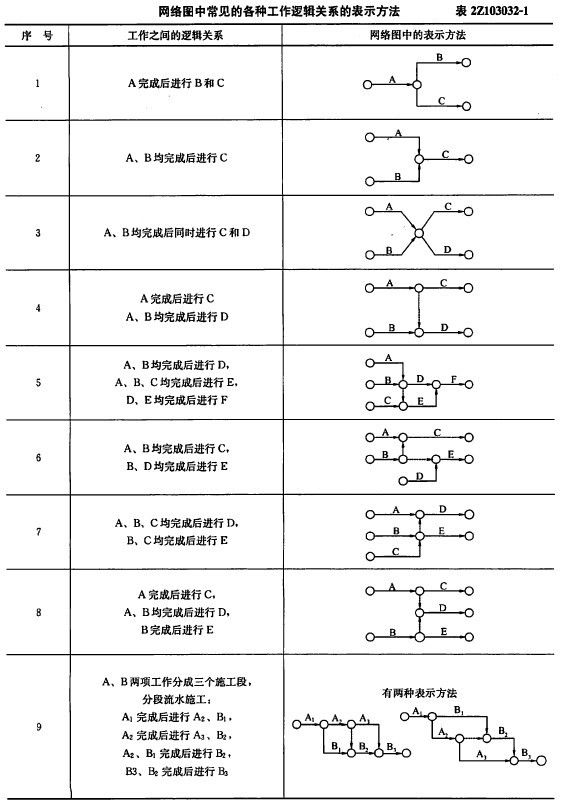
( 1 ) 双代号网络图必须正确表达已确定的逻辑关系。网络图中常见的各种工作逻辑关系的表示方法见表2Z103032-1 。
( 2 ) 双代号网络图中, 不允许出现循环回路。 所谓循环回路是指从网络图中的某一个节点出发, 顺着箭线方向又回到了原来出发点的线路。
( 3 ) 双代号网络图中, 在节点之间不能出现带双向箭头或无箭头的连线。
( 4 ) 双代号网络图中, 不能出现没有箭头节点或没有箭尾节点的箭线。
( 5 ) 当双代号网络图的某些节点有多条外向箭线或多条内向箭线时,为使图形简洁,可 使 用 母 线 法 绘 制 ( 但应 满足一项工作 用一条 箭 线 和 相应的一对节点表示),如图1Z203032-4 所示。
( 6 ) 绘制网络图时, 箭线不宜交叉。当交叉不可避免时,可用过桥法或指向法,如图1Z203032-5 所示。
( 7 ) 双代网络图中应只有一个起点节点和一个终点节点( 多目标阿络计划除外),而其他所有节点均应是中间节点。
( 8 ) 双代号网络图应条理清楚,布局合理。例如,网络图中的工作箭线不宜画成任意方向或曲线形状, 尽可能用水平线或斜线; 关键线路、 关键工作尽可能安排在图面中心位置 , 其他工作分散在两边; 避免倒回箭头等。
虚箭线
在双代号网络图中,为了正确地表达图中工作之间的逻辑关系, 往往需要应甩虚箭线。
虚箭线是实际工作中并不存在的一项虚设工作, 故它们既不占用肘间,也不消耗资源,一般起着工作之间的联系、区分和断路三个作用:
( 1 ) 联系作用是指应用虚箭线正确表达工作之间相互依存的关系;
( 2 ) 区分作用是指双代号网络图中每一项工作都必须用一条箭线和两个代号表示, 若两项工作的代号相同时, 应使用虚工作加以区分,如 图 1Z203032-3 所示;
( 3 ) 断路作用是用虚箭线断掉多余辱系,即在网络图中把无联系的工作连接上时, 应加上虚工作将其断开。
单代号网络图(节点型)
----用一个圆圈代表一项活动,箭线仅表示活动之间的逻辑关系。
关键路径上的工作:ES=LS,EF=LF
总时差TF=LS-ES=LF-EF(不影响总工期的情况下,我能玩多久,什么情况下不影响总工期 ?答案是:不影响关键路径上工作时间,我能玩多久)
自由时差FF=紧后工作ES最小值-本工作的EF
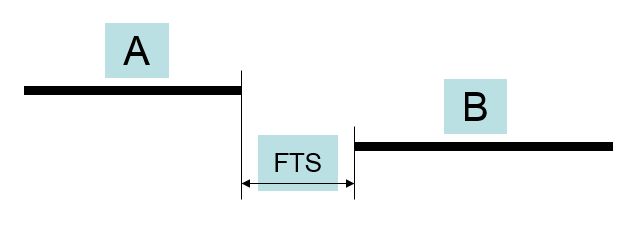
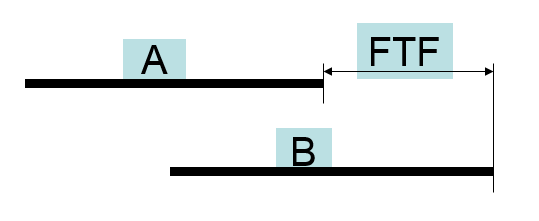
单代号网络图中的STS、STF、FTS、FTF
STS (start to start) 表示 :本工作最早开始时间与紧后工作最早开始时间之差; 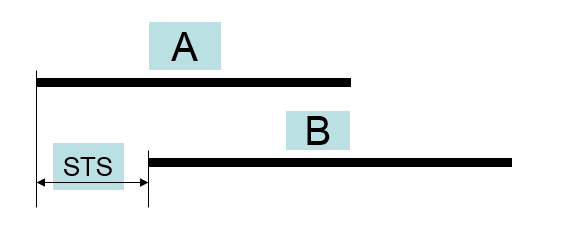
STF (start to finish) 表示 :本工作最早开始时间与紧后工作最早完成时间之差;

FTS ( finish to start) 表示 :本工作最早完成时间与紧后工作最早开始时间之差。
FTF (finish to finish) 表示 :本工作最早完成时间与紧后工作最早完成时间之差;
时标网络图
----时间标注的网络图
2 . 按工作的持续时间绘制①节点的外向箭线①〜②,即按人工作的持续时间,画出无紧前工作的皋工作, 确定节点②的位置。
3 . 自左至右依次确定其余各节点的位置。如②、③、④、⑥、⑨、 ⑩节点之前只有一条内向箭线,则在其内向箭线绘制完成后即可在其末端将上述节点绘出。⑤ 、⑦、⑧、⑩、 ⑫、 ⑬、 ⑭、 ⑮节点则必须待其前面的两条内向箭线都绘制完成后才能定位在这些内向箭线中最晚完成的时刻处。其中, ⑤、 ⑦、⑧ 、 ⑩ 、 ⑫、 ⑭各节点均有长度不足以达到该节点的内向实箭线, 故用波形线补足。
4 . 用上述方法自左至右依次确定其他节点位置,直至画出全部工作,确定终点节点⑮的位置, 该时标网络计划即绘制完成。
时标网络图的特点是:时间周期一目了然。
关键路径:①②③⑤⑥⑦⑩⑪⑫⑬⑮ 和 ①②③⑤⑥⑦⑩⑪⑫⑬⑭⑮
前锋线比较图
关键路径:①④⑥⑦⑧
工作进度在前锋线左边,表示进度滞后;在前锋线右边,表示进度超前。
第3周和第6周是检查点:
- 第3周的时候,工作A进度正好,工作B进度延后1周,工作C进度延后1周。
- 第6周的时候,工作D进度延后1周,工作E进度正好,工作G进度完成不影响工期。
假设工作D,由于业主方原因导致的;工作E,由于不可抗力导致的;工作C,由于承建方自己原因导致的。那么请问,工作D,是否可以向监理申请工期延后2周?
答案:不可以。由于甲方原因导致滞后,乙方只能向监理申请延后1周,因为D的总时差是1周。
那么请问,工作E,是否可以向监理申请工期延后1周?
答案:不可以,因为工作E的总时差是1周,延后1周不影响总工期。
那么请问,工作C,是否可以向监理申请工期延后2周?
答案:不可以,由于乙方原因造成的,由乙方加班、赶工自行完工,监理方不予申请工期延后。
非匀速进展横道网络图
--甘特图
图中要明白的含义:
实际开始时间,从第一周中间的时候开始的,连续施工的。
第1个周末,进度滞后2%
第2个周末,进度滞后3%
第3个周末,进度滞后3%
第4个周末,进度滞后5%
PERT(三点估算、完工概率计算)
三点估算定义
最可能时间tm、最乐观时间to、最悲观时间tp

活动持续时间/期望值te=(to+4*tm+tp)/6
持续时间标准差=(tp-t)/6;方差=标准差的平方
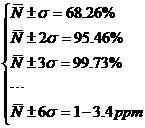
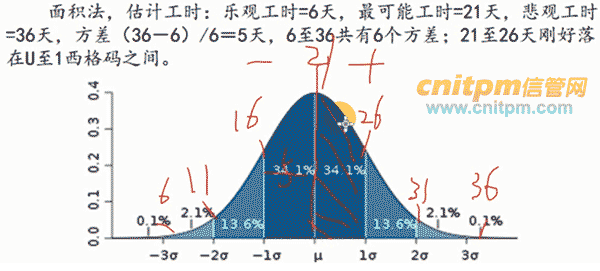
算完工概率(面积法解题): 68%,95%,99%,工程在估算工期前后 1 期间内完工的概率为 68% ,在估算工期前后 2 期间内完工的概率为 95% ,估算工期前后 3 期间内完工的概率为 99% 。
完工概率面积法例题
1、过去几年小李完成了大量网卡驱动模块的开发,最快6天完成,最慢36天完成,平均21天完成。如今小李开发一个新网卡驱动模块,在21天到26天内完成的概率是(B )。
A.68.3% B.34.1% C.58.2% D.28.1%
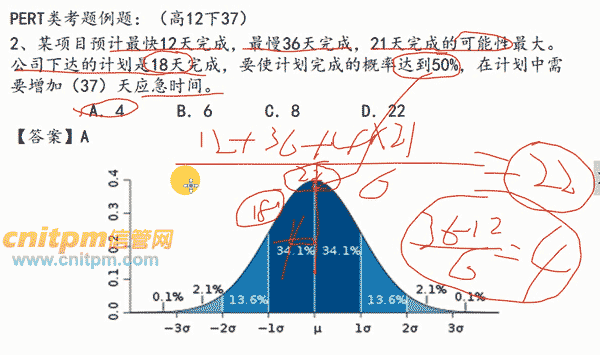
2、某项目预计最快12天完成,最慢36天完成,21天完成的可能性最大。公司下达的计划是18天完成,要使计划完成的概率达到50%,在计划中需要增加( A)天应急时间。
A.4 B.6 C.8 D.22
三点估算法求出期望工期=(12+4*21+36)/6=22,而期望工期是按时完工概率的50%,所以如果要18天完成,需要增加22-18=4天。
对于正态分布,期望值两边1个标准差的范围内,曲线下面积约占总面积的68%;2个标准差范围内,曲线下面积约占总面积的95%;3个标准差的范围内,曲线下面积约占总面积的99%。因此我们可以知道,项目在期望工期完成的概率是50%,在(期望工期+1个标准差)时间内完成的概率是(50%+(68%/2))=84%,在(期望工期+2个标准差)时间内完成的概率是(50%+(95%/2))=97.5%,在(期望工期+3个标准差)时间内完成的概率是(50%+(99%/2))=99.5%
3、例图:
活动BCD的乐观(m)工期都是9天,最可能(o)工期为12天,最悲观(p)工期都是15天,那么在14天内完成单项活动的概率和完成全部这三项活动的概率是多少?
首先计算平均工期(PERT):
公式--(乐观时间+4*最可能时间+悲观时间)/ 6
(9+4*12+15)/6=12天;
其次计算标准差:
公式--(悲观时间-乐观时间)/ 6 ;
(15-9)/6=1天
再计算偏离平均工期:
方法--[给出的天数计算(14)-计算出来的平均工期(12)]/标准差(1)
(14-12)/1=2
备注:此时得出来的为几,之后就是使用几西格玛(Sigma)(1σ=68,37%)(2σ=95.46%)(3σ=99.73%)(6σ=99.99966%百万分之三点四)
计算每一项活动在14天内完工的概率是:
方法--正态分布概率+西格玛/偏离平均工期数
0%+95.46%/2=97.73%
备注:50%参考正态分布图,95.46参考2西格玛值;
计算全部活动在14天内完工概率是:
方法--每一项活动的概率相乘
97.73%*97.73%*97.73%=93.34%
下图为简要正态分布图:
备注:正态分布有50%成功,有50%不成功
如计算将上面的14天,修改为13天;
偏离平均工期就是1天,计算方法:(13-12)/1=1天,则应该使用1西格玛;
计算每一项活动在13天内完工的概率是:
方法--正态分布概率+西格玛/偏离平均工期数
50%+68.37%/2=84.19%
备注:50%参考正态分布图,68.37参考1西格玛值;
计算全部活动在13天内完工概率是:
方法--每一项活动的概率相乘
84.19%*84.19%*84.19%=59.67%
如果计算为11-15天的概率:最小值的概率+最大值的概率
68.37/2+99.75/2=84.06%
完工概率排列组合法例题
某项目由并行的3个模块A、B和C组成,其中活动A需要3人5天时间完成,活动B需要6人7天时间完成,活动C需要4人2天时间完成。为了保证项目在最短时间内完成,则最少应该为项目组配置(35)人。假设活动A、B和C按时完成的概率分别多80%、70%和100%,则该项目按时完成的概率为(36)。
(35)A. 6 B. 9 C. 1 0 D. 13
(36)A.50% B. 56% C. 64% D. 90%.
解题分析:
问题(35):
1、为了保证项目在最短时间内完成====>找出项目完工关键路径。
活动A 5天 3人
活动B 7天 6人
活动C 2天 4人
活动A、B、C是并行进行的,所以关键路径是最长的完工时间 7天
2、列出活动A、B、C的总时差,活动总时差TF是指活动在不影响总工期的前提下,所具有的机动时间。
活动A 5天 3人 TF=2天
活动B 7天 6人 TF=0天
活动C 2天 4人 TF=5天
这里组合后可以知道:
A需要3人同时执行,B是关键路径这里不能动,C需要4人同时执行。
那么:
B、C先执行2天后,再将C的4人,调3个人去做A的工作,由于A的TF=2天,延后2天不影响总工期。
所以:
最少配置10人:6人+4人=10人
问题(36):
根据数学排列组合有加法原则、乘法原则:
项目按时完成的概率为:80% × 70% × 100% = 0.56=56%
总结:
关键路径:所有从开始到结束的路径中,活动历时之和最大的路径。
总工期:关键路径的活动历时之和。
最早开始时间ES:最早可能的开始时间
最早结束时间EF:EF=ES+D(本工作持续时间)
最晚结束时间LF:不影响总工期的结束时间
最晚开始时间LS:LS=LF-D(本工作持续时间)
总时差TF=LS-ES=LF-EF
自由时差FF=紧后工作的最小ES-此活动的EF