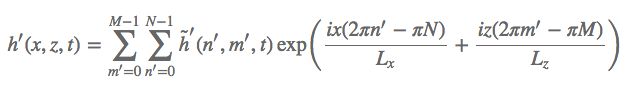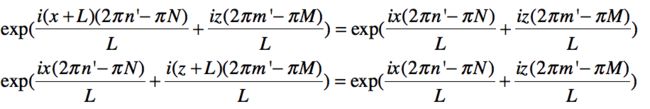针对这两篇教程:
http://www.keithlantz.net/2011/10/ocean-simulation-part-one-using-the-discrete-fourier-transform/
http://www.keithlantz.net/2011/11/ocean-simulation-part-two-using-the-fast-fourier-transform/
的一些注解:
一,
原文下面一段
框起部分不通顺,似乎应该是 "by letting Lx=N and Lz=M. then becomes,"
从这段之后教程中本应是Lx,Lz的地方就都变成M,N了。
由此看来,作者为了方便使用fft计算heightmap,强制使Lx,Lz等于M,N了。
而在教程的非fft的版本中是没有Lx,Lz必须等于N,M的限制的,甚至Lx,Lz可以不是整数。
即对于非fft版本,ocean的构造函数
cOcean::cOcean(const int N, const float A, const vector2 w, const float length, const bool geometry)
中N和length可以传不同的值,但对于fft版本,N和length必须传相同整数值才正确(N须为2的幂)。
补充:坑爹,原来我用的浏览器有问题,导致教程中插在句子中的数学符号显示不出来,刚才用另一个浏览器看,发现红框中那句确实是:
整篇教程中类似情况不胜枚举,我居然一直都是在缺符号的情况下看的。。。
二,
教程中h_tilde为NxN,vertices为(N+1)x(N+1)。
vertices的初始化代码为:
for (int m_prime = 0; m_prime < Nplus1; m_prime++) {
for (int n_prime = 0; n_prime < Nplus1; n_prime++) {
index = m_prime * Nplus1 + n_prime;
htilde0 = hTilde_0( n_prime, m_prime);
...
vertices[index].ox = vertices[index].x = (n_prime - N / 2.0f) * length / N;
vertices[index].oy = vertices[index].y = 0.0f;
vertices[index].oz = vertices[index].z = (m_prime - N / 2.0f) * length / N;
...
}
}
从中可以看出h'(x,z,t)的x和z的初始表达式为:
x=(n'-N/2)*L/N
z=(m'-N/2)*L/N
对于fft版本,由于教程中强制令L=N,所以
x=n'-N/2
z=m'-N/2
(注,后面为了实现“卷浪”,x,z在此基础上还会进行一定的偏移)。
三,
教程中fft版本的总体计算思路是将二维DFT:
拆成两个一维DFT来进行计算
以N=4为例,计算过程如下:
其中DFT(4)代表(4)式所定义的DFT,DFT(3)代表(3)式所定义的DFT。
即先逐行dft,再逐列dft。
可见对于N=4的情况,完成heightmap的更新需要计算8个DFT,那么对于一般情况则需要计算2N个DFT。
每个DFT都可以使用FFT来计算,对应教程中如下代码:
for (int m_prime = 0; m_prime < N; m_prime++) {
fft->fft(h_tilde, h_tilde, 1, m_prime * N);
…
}
for (int n_prime = 0; n_prime < N; n_prime++) {
fft->fft(h_tilde, h_tilde, N, n_prime);
…
}
四,
教程代码中实现无缝循环(tiling)的代码非常简单,只是将第0行(列)的数据填充给第N+1行(列)即可:
for (int m_prime = 0; m_prime < N; m_prime++) {
for (int n_prime = 0; n_prime < N; n_prime++) {
index = m_prime * N + n_prime; // index into h_tilde..
index1 = m_prime * Nplus1 + n_prime; // index into vertices
…
// height
vertices[index1].y = h_tilde[index].a;
…
// for tiling
if (n_prime == 0 && m_prime == 0) {
vertices[index1 + N + Nplus1 * N].y = h_tilde[index].a;
…
}
if (n_prime == 0) {
vertices[index1 + N].y = h_tilde[index].a;
…
}
if (m_prime == 0) {
vertices[index1 + Nplus1 * N].y = h_tilde[index].a;
…
}
}
}
言外之意,h'(x,z,t)在x和z方向上均是以L为周期的周期函数,即:
h'(x+L,z,t)=h(x,z,t)
h'(x,z+L,t)=h(x,z,t)
事实确实如此,验证如下:
因为N为偶数,所以
所以
h'(x+L,z,t)=h(x,z,t)
h'(x,z+L,t)=h(x,z,t)
五,
evaluateWavesFFT函数中如下代码:
for (int m_prime = 0; m_prime < N; m_prime++) {
fft->fft(h_tilde, h_tilde, 1, m_prime * N);
…
}
for (int n_prime = 0; n_prime < N; n_prime++) {
fft->fft(h_tilde, h_tilde, N, n_prime);
…
}
int sign;
float signs[] = { 1.0f, -1.0f };
vector3 n;
for (int m_prime = 0; m_prime < N; m_prime++) {
for (int n_prime = 0; n_prime < N; n_prime++) {
index = m_prime * N + n_prime; // index into h_tilde..
index1 = m_prime * Nplus1 + n_prime; // index into vertices
sign = signs[(n_prime + m_prime) & 1];//如果n+m为奇数,则sign=signs[1]=-1;如果n+m为偶数,则sign=signs[0]=1
h_tilde[index] = h_tilde[index] * sign;
…
}
}
可见在计算完2N次FFT后,还有一个符号校正(乘以sign)的步骤。
为什么需要符号校正?
因为代码中的第一个fft并不是完整计算了h''(x,m',t),而只是计算了下式中红框内的部分(省略了一个(-1)^x因子):
同理,代码中的第二个fft也并不是完整计算了h'(x,z,t),而只是计算了下式中红框内的部分(省略了一个(-1)^z因子):
所以当fft计算全部执行完后,还需要乘以(-1)^(x+z)。
因为在fft版本中x=n'-N/2,z=m'-N/2,所以(-1)^(x+z)=(-1)^(n'+m'-N),因为N为偶数,所以(-1)^(n'+m'-N)=(-1)^(n'+m')。
六,
蝶形图及T函数表实现
这一块发现教程中有些错误,我们自己来推导一下N=4的蝶形图。
在上式中令N=4,得:
因x=n'-N/2,n'=0,1,2,3,所以x=-2,-1,0,1,并适当利用 变形,得:
变形,得:
据此可画出蝶形图:
对上面蝶形图进行等价优化变形,得:
注:以上优化变形的原理是:因为 ,所以有T4^0=-T4^(-2),故可将T4^(-2)由支干移至主干,并将T4^0改为-1。同理,可将T4^(-1)由支干移至主干,并将T4^1改为-1。
,所以有T4^0=-T4^(-2),故可将T4^(-2)由支干移至主干,并将T4^0改为-1。同理,可将T4^(-1)由支干移至主干,并将T4^1改为-1。
容易看出变换后的蝶形图与原蝶形图等价。此优化思路源于:https://cnx.org/contents/zmcmahhR@7/Decimation-in-time-DIT-Radix-2,其中的Additional Simplification一节。
此即为N=4时的最终蝶形图,可以验证此蝶形图与教程中给出的N=4蝶形图是不等价的,即教程中蝶形图有误。
再看教程中生成T函数表的代码:
cFFT::cFFT(unsigned int N) : N(N), reversed(0), T(0), pi2(2 * M_PI) {
…
int pow2 = 1;
T = new complex*[log_2_N]; // prep T
for (int i = 0; i < log_2_N; i++) {
T[i] = new complex[pow2];
for (int j = 0; j < pow2; j++) T[i][j] = t(j, pow2 * 2);
pow2 *= 2;
}
…
}
complex cFFT::t(unsigned int x, unsigned int N) {
return complex(cos(pi2 * x / N), sin(pi2 * x / N));
}
显然也是有错误的,其中
for (int j = 0; j < pow2; j++) T[i][j] = t(j, pow2 * 2);
一句,应改为:
for (int j = 0; j < pow2; j++) T[i][j] = t(j-N/2, pow2 * 2);
因为x=n'-N/2,而非x=n'。
此至,教程及代码中的疑问基本上就都解决了,下面是移植到unity中的结果:
(为了确认无缝,在z轴方向平铺了一次)
----补充:
一,
蝶形图的含义:
首先我们知道蝶形图右边任何一个输出都是左边所有输入的线性组合,所以假设我们想知道h'''(-1,m',t)的表达式,首先有
然后再根据蝶形图读出A,B,C,D的值。
求A的值,看红色路径,没有经过任何值,所以A=1。
求B的值,看绿色路径,经过T2^(-2)和-1,所以B=-T2^(-2)。
求C的值,看蓝色路径,经过T4^(-1),所以C=T4^(-1)。
求D的值,看黄色路径,经过T2^(-2),-1,T4^(-1),所以D=-T2^(-2)*T4^(-1)。
所以得:
对比前面(六)中所得:
因为-T2^(-2)=T2^(-1),所以结果是一样的。
二,
比特翻转
根据蝶形图实现fft,因为蝶形图左边N个输入数据的是乱序(比如对于N=4而言是0,2,1,3;对于N=8而言是0,4,2,6,1,5,3,7),这个次序可由bit reverse来生成,以N=4为例:
0 (00) -- bit reverse --> (00) 0
1 (01) -- bit reverse --> (10) 2
2 (10) -- bit reverse --> (01) 1
3 (11) -- bit reverse --> (11) 3
参考:http://www.dspguide.com/ch12/2.htm
代码中实现bit reverse的部分为:
cFFT::cFFT(unsigned int N) : N(N), reversed(0), T(0), pi2(2 * M_PI) {
…
log_2_N = log(N)/log(2);
reversed = new unsigned int[N]; // prep bit reversals
for (int i = 0; i < N; i++) reversed[i] = reverse(i);
…
}
unsigned int cFFT::reverse(unsigned int i) {
unsigned int res = 0;
for (int j = 0; j < log_2_N; j++) {
res = (res << 1) + (i & 1);
i >>= 1;
}
return res;
}
----补充2
此教程为cpu实现fft ocean,且fft部分的实现方法用的是最直观的方法,所以效率是比较不高的方法。
但即使cpu fft ocean再怎么优化,效果肯定也高不到哪儿去,所以此教程仅作为一个起点。接下来移植到gpu是必须的。等移植完我再另写一篇日志。
2017-6-25更新:
基于gpu的实现已初步试验成功,见下帖中的2017-6-25:http://www.cnblogs.com/wantnon/p/6985141.html
2017-6-30更新:
gpu fft海面动画已实现,见下帖中的2017-6-30: http://www.cnblogs.com/wantnon/p/6985141.html
----
另附两个重要参考:
http://graphics.ucsd.edu/courses/rendering/2005/jdewall/tessendorf.pdf
https://pdfs.semanticscholar.org/0047/8af7044a7f1350d5ec75ffc7c15b40057051.pdf