(16)[ICLR15] ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION
计划完成深度学习入门的126篇论文第十六篇,多伦多大学Jimmy Lei Ba和OpenAI的Ilya Diederik P. Kingma合作研究一种在梯度下降过程中优化下降迭代速度的方式,结合AdaGradRMSProp,和属于AdaptiveLearning的一种。关联:Momentum,AdaGrad,RMSProp,Adabound。
ABSTRACT&INTRODUCTION
摘要
介绍了一种基于低阶矩自适应估计的随机目标函数一阶梯度优化算法Adam。该方法易于实现,计算效率高,内存需求小,对梯度的对角重新标度不变,并且非常适合于数据和/或参数很大的问题。该方法也适用于非平稳目标和具有非常嘈杂和/或稀疏梯度的问题。超参数有直观的解释,通常不需要太多的调优。讨论了一些与相关算法的联系,Adam就是在这些算法上受到启发的。分析了该算法的理论收敛性,给出了与在线凸优化框架下最优解收敛速度相当的遗憾。实验结果表明,该方法在实际应用中效果良好,与其他随机优化方法相比具有一定的优越性。最后,我们讨论Adammax,是基于无限范数Adam的一个变种。
介绍
基于随机梯度的优化方法在许多科学和工程领域具有重要的实际意义。这些领域中的许多问题都可以转化为一个标量参数化目标函数的优化问题,该目标函数的参数要求最大或最小。如果函数的参数是可微的w.r.t,梯度下降法是一种比较有效的优化方法,因为一阶偏导数w.r.t的计算,所有参数的计算复杂度都与函数的求值相同。通常,目标函数是随机的。例如,许多目标函数由一组子函数和组成,这些子函数在不同的数据子样本上求值;在这种情况下,优化可以更有效地采取梯度步骤w.r.t.单独的子函数,即随机梯度下降(SGD)或上升。SGD证明了自己是一种高效和有效的优化方法,这在许多机器学习成功的故事中都是核心,比如最近在深度学习方面的进展(Deng et al., 2013; Krizhevsky, 2012; Hinton, Salakhutdinov, 2006;Hinton, 2012a; Graves, 2013)。目标也可能有数据子采样以外的其他噪声源,如dropout (Hinton et al., 2012b)正则化。对于所有这些噪声目标,都需要有效的随机优化技术。本文主要研究具有高维参数空间的随机目标的优化问题。在这种情况下,高阶优化方法是不合适的,本文的讨论将局限于一阶优化方法。
提出了一种只需要一阶梯度且内存要求小的高效随机优化方法Adam。该方法通过对梯度的一阶矩和二阶矩的估计,计算不同参数的个体自适应学习率;Adam这个名字来源于adaptive moment estimation。我们的方法结合了两种最近流行的方法的优点AdaGrad (Duchi et al., 2011)和RMSProp (Tieleman&Hinton, 2012),在在线和非平稳设置下工作良好;第5节阐明了这些方法和其他随机优化方法之间的重要联系。Adam的一些优点是,参数更新的大小对梯度的重新标度是不变的,其步长近似受步长超参数的约束,不需要平稳目标,使用稀疏梯度,自然地执行一种步长退火形式。
第二部分介绍了该算法及其更新规则的性质。第3节解释了我们的初始化偏差校正技术,第4节对Adam在在线凸规划中的收敛性进行了理论分析。从经验上看,我们的方法在各种模型和数据集上始终优于其他方法,如第6节所示。总的来说,我们证明了Adam是一个通用的算法,它可以扩展到大规模的高维机器学习问题。
ALGORITHM
我们提出的算法Adam的伪代码见算法1。![]() 是一个嘈杂的目标函数:一个随机标量函数可微的w.r.t.参数θ。我们感兴趣的是最小化这个函数的期望值,
是一个嘈杂的目标函数:一个随机标量函数可微的w.r.t.参数θ。我们感兴趣的是最小化这个函数的期望值,![]() w.r.t.是他的参数θ。与
w.r.t.是他的参数θ。与![]() 我们表示随机函数的实现。在随后的步数
我们表示随机函数的实现。在随后的步数![]() 中。随机性可能来自随机子样本(小批量)的数据点评价,也可能来自固有的函数噪声。
中。随机性可能来自随机子样本(小批量)的数据点评价,也可能来自固有的函数噪声。![]() 我们表示梯度,即在步伐t评估向量
我们表示梯度,即在步伐t评估向量![]() 偏导数w.r.t 。
偏导数w.r.t 。
梯度的算法更新exponential moving averages(mt)和的平方梯度(vt) hyper-parameters![]() 控制这些移动平均线的指数衰减率。moving averages本身是梯度的第一个矩(平均值)和第二个原始矩(无中心方差)的估计。然而,这些moving averages初始化为0(向量),估计是偏向零导致的时刻,特别是在最初的步伐,特别是当衰变速率很小(即βs接近1)。好消息是,这可以很容易地抵消的初始偏差,bias-corrected估计
控制这些移动平均线的指数衰减率。moving averages本身是梯度的第一个矩(平均值)和第二个原始矩(无中心方差)的估计。然而,这些moving averages初始化为0(向量),估计是偏向零导致的时刻,特别是在最初的步伐,特别是当衰变速率很小(即βs接近1)。好消息是,这可以很容易地抵消的初始偏差,bias-corrected估计![]() 。更多细节见第3节。
。更多细节见第3节。
请注意,算法1的效率可以通过改变计算顺序来提高,例如用以下几行替换循环中的最后三行:
![]()
ADAM’S UPDATE RULE
Adam的update规则的一个重要属性是它对步长的谨慎选择。假设![]() ,则第t时刻在参数空间中所采取的有效步长为
,则第t时刻在参数空间中所采取的有效步长为![]() 。
。
有效步长有两个上界:![]() ,
,![]() ,
,![]() 。第一种情况只发生在最严重的稀疏情况下:当梯度在除当前时间步长以外的所有时间步长为零时。对于较少稀疏的情况,有效步长会更小。当
。第一种情况只发生在最严重的稀疏情况下:当梯度在除当前时间步长以外的所有时间步长为零时。对于较少稀疏的情况,有效步长会更小。当![]() 时,我们有
时,我们有![]() ,所以
,所以![]() 。在更常见的情况下,我们会遇到这种情况
。在更常见的情况下,我们会遇到这种情况![]() 。
。
有效的步骤在参数空间的大小在每个步伐大约有界的stepsize设置α,即![]() 。这可以理解为围绕当前参数值建立一个信任区域,超过这个信任区域,当前梯度估计就不能提供足够的信息。这通常使它相对容易知道正确的
。这可以理解为围绕当前参数值建立一个信任区域,超过这个信任区域,当前梯度估计就不能提供足够的信息。这通常使它相对容易知道正确的![]() 的大小。例如,对于许多机器学习模型,我们通常预先知道,在参数空间的某个集合区域内,良好的最优解具有很高的概率;例如,对参数进行先验分布并不少见。自α集(上界)步骤在参数空间的大小,我们经常可以推断出正确的数量级内从
的大小。例如,对于许多机器学习模型,我们通常预先知道,在参数空间的某个集合区域内,良好的最优解具有很高的概率;例如,对参数进行先验分布并不少见。自α集(上界)步骤在参数空间的大小,我们经常可以推断出正确的数量级内从![]() ,这样可以达到最佳状态的迭代次数。
,这样可以达到最佳状态的迭代次数。
稍微滥用一下术语,我们将比率![]() 称为信噪比(SNR)。信噪比越小,有效步长t越接近于零。这是一个理想的性质,因为较小的信噪比意味着对于
称为信噪比(SNR)。信噪比越小,有效步长t越接近于零。这是一个理想的性质,因为较小的信噪比意味着对于![]() 的方向是否与真实梯度的方向相对应存在较大的不确定性。例如,SNR值通常会趋近于0,趋近于一个最优值,从而导致参数空间中更小的有效步骤:一种自动退火形式。有效步长t也不随梯度的大小而变化:用因子c重新标定梯度g将用因子c缩放
的方向是否与真实梯度的方向相对应存在较大的不确定性。例如,SNR值通常会趋近于0,趋近于一个最优值,从而导致参数空间中更小的有效步骤:一种自动退火形式。有效步长t也不随梯度的大小而变化:用因子c重新标定梯度g将用因子c缩放![]() ,用因子
,用因子![]() 缩放
缩放![]() ,两者抵消:
,两者抵消:![]() 。
。
INITIALIZATION BIAS CORRECTION
正如第2节所解释的,Adam使用了初始化偏差校正术语。我们将在这里推导出第二个矩估计的项;第一个矩估计的推导是完全类似的。让g f的梯度随机目标,和我们希望估计第二生时刻(偏心方差)使用一个指数移动平均线的平方梯度,与衰变率β2。让![]() 为后续时间步长的梯度,每个梯度都是从底层梯度分布
为后续时间步长的梯度,每个梯度都是从底层梯度分布![]() 中提取。让我们初始化指数移动平均为
中提取。让我们初始化指数移动平均为![]() (一个0向量)。首先注意,更新的步伐t指数移动平均
(一个0向量)。首先注意,更新的步伐t指数移动平均![]() 。表明element-wise平方
。表明element-wise平方![]() 可以写成一个函数的梯度之前的步伐:
可以写成一个函数的梯度之前的步伐:
我们想知道![]() ,即t时刻指数移动平均的期望值,与真实的第二阶矩
,即t时刻指数移动平均的期望值,与真实的第二阶矩![]() 之间的关系,这样我们就可以校正两者之间的误差。对上式的左右两边取期望:
之间的关系,这样我们就可以校正两者之间的误差。对上式的左右两边取期望:
ζ= 0如果真正的二阶矩![]() 是静止的;否则ζ可以保持小因为指数衰减率β1可以(而且应该)被选中,这样指数移动平均分配小权重梯度过去太远。剩下的词
是静止的;否则ζ可以保持小因为指数衰减率β1可以(而且应该)被选中,这样指数移动平均分配小权重梯度过去太远。剩下的词![]() 是由初始化运行平均零。因此,在算法1中,我们除以这一项来纠正初始化偏差correct bias。
是由初始化运行平均零。因此,在算法1中,我们除以这一项来纠正初始化偏差correct bias。
在稀疏的梯度的情况下,二次矩的一个可靠的估计需要平均在许多β2梯度通过选择一个小值,然而正是这种情况下的小β2初始化偏差纠正的缺乏将会导致更大的初始步骤。
CONVERGENCE ANALYSIS
我们使用Zinkevich(2003)提出的在线学习框架来分析Adam的收敛性。给定任意未知序列凸成本函数![]() 。在每个时间t,我们的目标是预测参数θt和评估未知的成本函数
。在每个时间t,我们的目标是预测参数θt和评估未知的成本函数![]() 。由于事先未知序列的性质,我们评估我们的算法使用regret,这是前面的区别的总和在线预测
。由于事先未知序列的性质,我们评估我们的算法使用regret,这是前面的区别的总和在线预测![]() 和最好的定点参数
和最好的定点参数![]() 从一个可行集合X前面的步骤。具体地说,遗憾的定义是:
从一个可行集合X前面的步骤。具体地说,遗憾的定义是:
![]() 。
。
![(16)[ICLR15] ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION_第1张图片](http://img.e-com-net.com/image/info8/3c45e7a3ac764beba3cf33e70fca8379.jpg)
![(16)[ICLR15] ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION_第2张图片](http://img.e-com-net.com/image/info8/f5ea732912294e2fafcc3de4cb170e8a.jpg)
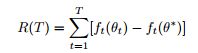
![(16)[ICLR15] ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION_第3张图片](http://img.e-com-net.com/image/info8/4d7cebb43444410f97fa7bdf8126f65d.jpg)
![(16)[ICLR15] ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION_第4张图片](http://img.e-com-net.com/image/info8/9dad18559f994050bf0ca9ea7240e3ed.jpg)
![(16)[ICLR15] ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION_第5张图片](http://img.e-com-net.com/image/info8/b2f6961b7ca54ef8baf3cdd75d5bbcf6.jpg)
![(16)[ICLR15] ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION_第6张图片](http://img.e-com-net.com/image/info8/efcc9e3cbbd74c85aae34639fd5ae183.jpg)