2015年第六届蓝桥杯省赛试题及详解(Java本科B组)
蓝桥杯历年真题题目及题解目录汇总
- 结果填空 (满分3分)
- 结果填空 (满分5分)
- 结果填空 (满分9分)
- 代码填空 (满分11分)
- 代码填空 (满分15分)
- 结果填空 (满分17分)
- 结果填空 (满分21分)
- 程序设计(满分13分)
- 程序设计(满分25分)
- 程序设计(满分31分)
1.三角形面积
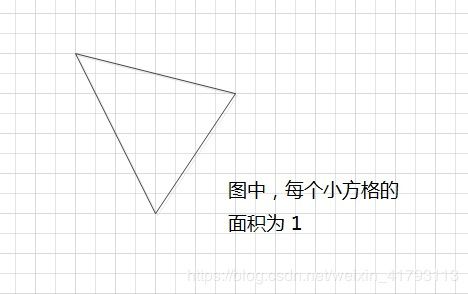
如图1所示。图中的所有小方格面积都是1。
那么,图中的三角形面积应该是多少呢?
请填写三角形的面积。不要填写任何多余内容或说明性文字。
思路:矩形减去3个三角形面积 8*8 - 0.5*8*4 - 0.5*4*6 - 0.5*8*2 答案:28
2.立方变自身
观察下面的现象,某个数字的立方,按位累加仍然等于自身。
1^3 = 1
8^3 = 512 5+1+2=8
17^3 = 4913 4+9+1+3=17
...
请你计算包括1,8,17在内,符合这个性质的正整数一共有多少个?
请填写该数字,不要填写任何多余的内容或说明性的文字。
答案:6,暴力枚举1到10000,打印观察,发现最大的数只是到27,没必要再扩大枚举的范围了,6已是答案
public class _02立方变自身1 {
public static void main(String[] args) {
int ans = 0;
for(int i=1;i<=10000;i++) {
if(i==f(i*i*i)) {
System.out.println(":"+i);
ans++;
}
}
System.out.println(ans);
}
static int f(int x) {
int ans=0;
while(x>0) {
ans+=x%10;
x/=10;
}
return ans;
}
}
3.三羊献瑞
观察下面的加法算式:
祥 瑞 生 辉
+ 三 羊 献 瑞
-------------------
三 羊 生 瑞 气
(如果有对齐问题,可以参看【图1.jpg】)
其中,相同的汉字代表相同的数字,不同的汉字代表不同的数字。
请你填写“三羊献瑞”所代表的4位数字(答案唯一),不要填写任何多余内容。
这种0-9不同数字的枚举,直接暴力就好,不过感觉暴力也要写挺久的,也可以试下全排,答案:1085
public class _03三羊献瑞_ {
public static void main(String[] args) {
for(int x1=0;x1<10;x1++)
for(int x2=0;x2<10;x2++) {
if(x1==x2)
continue;
for(int x3=0;x3<10;x3++) {
if(x3==x1 || x3==x2)
continue;
for(int x4=0;x4<10;x4++) {
if(x4==x1 || x4==x2 || x4==x3)
continue;
for(int x5=0;x5<10;x5++) {
if(x5==x1 || x5==x2 || x5==x3 || x5==x4)
continue;
for(int x6=0;x6<10;x6++) {
if(x6==x1 || x6==x2 || x6==x3 || x6==x4 || x6==x5)
continue;
for(int x7=0;x7<10;x7++) {
if(x7==x1 || x7==x2 || x7==x3 || x7==x4 || x7==x5 || x7==x6)
continue;
for(int x8=0;x8<10;x8++) {
if(x8==x1 || x8==x2 || x8==x3 || x8==x4 || x8==x5 || x8==x6 || x8==x7)
continue;
if(x1==0 || x5==0)
continue;
int x = 1000*x1 + 100*x2 + 10*x3 + x4;
int y = 1000*x5 + 100*x6 + 10*x7 + x2;
int z = 10000*x5 + 1000*x6 + 100*x3 + 10*x2 + x8;
if(x+y==z) {
System.out.println(x+"+"+y+"=="+z);
System.out.println(x1+" "+x2+" "+x3+" "+x4+" "+x5+" "+x6+" "+x7+" "+x8+" ");
}
}
}
}
}
}
}
}
}
}全排的话直接截取前8个数就好,写起来比上面8个for要舒爽,不过直觉上感觉8个for稳一点org
public class _03三羊献瑞_全排 {
public static void main(String[] args) {
dfs(0);
}
static int[] a = new int [] {0,1,2,3,4,5,6,7,8,9};
static void dfs(int m) {
if(m>=10) {
int x = 1000*a[0] + 100*a[1] + 10*a[2] + a[3];
int y = 1000*a[4] + 100*a[5] + 10*a[6] + a[1];
int z = 10000*a[4] + 1000*a[5] + 100*a[2] + 10*a[1] + a[7];
if(a[0]==0 || a[4]==0)
return;
if(x+y==z)
System.out.println(x+"+"+y+"=="+z);
return;
}
for(int i=m;i<10;i++) {
swap(i,m);
dfs(m+1);
swap(i,m);
}
}
static void swap(int i,int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
}
4.循环节长度
两个整数做除法,有时会产生循环小数,其循环部分称为:循环节。
比如,11/13=6=>0.846153846153..... 其循环节为[846153] 共有6位。
下面的方法,可以求出循环节的长度。
请仔细阅读代码,并填写划线部分缺少的代码。
public static int f(int n, int m)
{
n = n % m;
Vector v = new Vector();
for(;;)
{
v.add(n);
n *= 10;
n = n % m;
if(n==0) return 0;
if(v.indexOf(n)>=0) _________________________________ ; //填空
}
}注意,只能填写缺少的部分,不要重复抄写已有代码。不要填写任何多余的文字。
return v.size() - v.indexOf(n);差点没看到v.add(),这里直接填v.size()是不对的比如7/18 0.3888888 但他会输出2,而应该是1,所以要减去第一个重复字母的下标
5.九数组分数
1,2,3...9 这九个数字组成一个分数,其值恰好为1/3,如何组法?
下面的程序实现了该功能,请填写划线部分缺失的代码。
public class A
{
public static void test(int[] x)
{
int a = x[0]*1000 + x[1]*100 + x[2]*10 + x[3];
int b = x[4]*10000 + x[5]*1000 + x[6]*100 + x[7]*10 + x[8];
if(a*3==b) System.out.println(a + " " + b);
}
public static void f(int[] x, int k)
{
if(k>=x.length){
test(x);
return;
}
for(int i=k; i注意,只能填写缺少的部分,不要重复抄写已有代码。不要填写任何多余的文字。
答案:{int t=x[k]; x[k]=x[i]; x[i]=t;},全排,回溯
6.加法变乘法
我们都知道:1+2+3+ ... + 49 = 1225
现在要求你把其中两个不相邻的加号变成乘号,使得结果为2015
比如:
1+2+3+...+10*11+12+...+27*28+29+...+49 = 2015
就是符合要求的答案。
请你寻找另外一个可能的答案,并把位置靠前的那个乘号左边的数字提交(对于示例,就是提交10)。
注意:需要你提交的是一个整数,不要填写任何多余的内容。
答案:16,看错题目了,还想用下前缀和,这里模拟,先减去这4个改变的数,再加入2个乘积的结果
public class _06__加法变乘法 {
public static void main(String[] args) {
int[] sum = new int[50];
for(int i=1;i<=49;i++)
sum[i]=sum[i-1]+i;
for(int i=1;i<49;i++)
for(int j=i+1;j<49;j++) {//i+2是最符合题意的,不相邻嘛,不过没关系打印观察
int ans = 1225;
ans = ans -(i+i+1);
ans = ans -(j+j+1);
ans = ans + i*(i+1)+j*(j+1);
if(ans==2015)
System.out.println(i+" "+j);
}
}
}
7.牌型种数
小明被劫持到X赌城,被迫与其他3人玩牌。
一副扑克牌(去掉大小王牌,共52张),均匀发给4个人,每个人13张。
这时,小明脑子里突然冒出一个问题:
如果不考虑花色,只考虑点数,也不考虑自己得到的牌的先后顺序,自己手里能拿到的初始牌型组合一共有多少种呢?
请填写该整数,不要填写任何多余的内容或说明文字。
答案:3598180
考点递归,其实前面一直下来都没考到dp和递归,从这角度想,应该会用到了把,不过我是暴力模拟到开头就发现可以递归了org,这里呢,每种纸牌有5种取法,有13种纸牌,可以选择取1个,取2个,取3个,取4个,取0个,注意不取的情况一定不能漏qaq,第一次漏了,粗心鸭= =,所以考试记得回头检查
static int f(int n,int m) {
if(n==0)
return m==0?1:0;
if(m==0)//这个属于剪枝把,填空题没有也没事
return 1;
if(m<0)//边界判断
return 0;
return f(n-1,m) + f(n-1,m-1) + f(n-1,m-2) +f(n-1,m-3)+f(n-1,m-4);
}网上的暴力枚举代码也是挺可爱的,可以学习下,重点是稳hhha,我们不差时间哈~
#include
using namespace std;
int main()
{
int sum=0;
for(int a=0; a<=4; a++)
for(int b=0; b<=4; b++)
for(int c=0; c<=4; c++)
for(int d=0; d<=4; d++)
for(int e=0; e<=4; e++)
for(int f=0; f<=4; f++)
for(int g=0; g<=4; g++)
for(int h=0; h<=4; h++)
for(int i=0; i<=4; i++)
for(int j=0; j<=4; j++)
for(int k=0; k<=4; k++)
for(int l=0; l<=4; l++)
for(int m=0; m<=4; m++)
{
if(a+b+c+d+e+f+g+h+i+j+k+l+m==13)
sum++;
}
cout<
8.饮料换购
乐羊羊饮料厂正在举办一次促销优惠活动。乐羊羊C型饮料,凭3个瓶盖可以再换一瓶C型饮料,并且可以一直循环下去,但不允许赊账。
请你计算一下,如果小明不浪费瓶盖,尽量地参加活动,那么,对于他初始买入的n瓶饮料,最后他一共能得到多少瓶饮料。
输入:一个整数n,表示开始购买的饮料数量(0
例如:
用户输入:
100
程序应该输出:
149
用户输入:
101
程序应该输出:
151
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
问题 1072: 汽水瓶之前做到过一题,比这题难一点的,区别是这题可以先借给你一瓶汽水,意思是最后2个瓶盖也可以换一瓶,
这2题的做法都是递归+直接模拟= =
import java.util.Scanner;
public class _08饮料换购_ {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
System.out.println(n+f(n));
}
static int f(int n) {
if(n<3)
return 0;
return n/3+f(n%3+n/3);
}
}注意下面代码是相似题的,并不是饮料换购,原题链接:问题 1072: 汽水瓶
/**
* http://www.dotcpp.com/oj/problem1072.html
* @author 叶
*
*/
//有这样一道智力题:“某商店规定:三个空汽水瓶可以换一瓶汽水。小张手上有十个空汽水瓶,
//她最多可以换多少瓶汽水喝?”答案是5瓶,方法如下:先用9个空瓶子换3瓶汽水,喝掉3瓶满的,
//喝完以后4个空瓶子,用3个再换一瓶,喝掉这瓶满的,这时候剩2个空瓶子。然后你让老板先借给你一瓶汽水
//,喝掉这瓶满的,喝完以后用3个空瓶子换一瓶满的还给老板。
//如果小张手上有n个空汽水瓶,最多可以换多少瓶汽水喝?
import java.util.Scanner;
public class 汽水瓶 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
for(int i=0;i<10;i++)
{
int x = in.nextInt();
if(x!=0)
System.out.println(f(x));
else
break;
}
}
static int f(int x)
{
if(x<2)
return 0;
return 1+f(x-2);
}
}
9.垒骰子
赌圣atm晚年迷恋上了垒骰子,就是把骰子一个垒在另一个上边,不能歪歪扭扭,要垒成方柱体。
经过长期观察,atm 发现了稳定骰子的奥秘:有些数字的面贴着会互相排斥!
我们先来规范一下骰子:1 的对面是 4,2 的对面是 5,3 的对面是 6。
假设有 m 组互斥现象,每组中的那两个数字的面紧贴在一起,骰子就不能稳定的垒起来。 atm想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同,当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多,请输出模 10^9 + 7 的结果。
不要小看了 atm 的骰子数量哦~
「输入格式」
第一行两个整数 n m
n表示骰子数目
接下来 m 行,每行两个整数 a b ,表示 a 和 b 不能紧贴在一起。
「输出格式」
一行一个数,表示答案模 10^9 + 7 的结果。
「样例输入」
2 1
1 2
「样例输出」
544
「数据范围」
对于 30% 的数据:n <= 5
对于 60% 的数据:n <= 100
对于 100% 的数据:0 < n <= 10^9, m <= 36
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
前面的题目都比较水,到了第九题,突然难度上去了,不过这题60%的数据还是很小的,可以试试拼一波暴力,30%的数据就更离谱了,n<=5,读懂题应该就能拿下了,考点:dp+快速幂+矩阵快速幂
import java.util.Scanner;
/*
垒骰子
赌圣atm晚年迷恋上了垒骰子,就是把骰子一个垒在另一个上边,不能歪歪扭扭,要垒成方柱体。
经过长期观察,atm 发现了稳定骰子的奥秘:有些数字的面贴着会互相排斥!
我们先来规范一下骰子:1 的对面是 4,2 的对面是 5,3 的对面是 6。
假设有 m 组互斥现象,每组中的那两个数字的面紧贴在一起,骰子就不能稳定的垒起来。 atm想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同,当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多,请输出模 10^9 + 7 的结果。
不要小看了 atm 的骰子数量哦~
「输入格式」
第一行两个整数 n m
n表示骰子数目
接下来 m 行,每行两个整数 a b ,表示 a 和 b 不能紧贴在一起。
「输出格式」
一行一个数,表示答案模 10^9 + 7 的结果。
「样例输入」
2 1
1 2
「样例输出」
544
「数据范围」
对于 30% 的数据:n <= 5
对于 60% 的数据:n <= 100
对于 100% 的数据:0 < n <= 10^9, m <= 36
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
*/
public class _09_垒骰子 {
static int op[] = new int[7];
private static int n;
private static int m;
private static final long MOD = 1000000007;
static void init() {
op[1] = 4;
op[4] = 1;
op[2] = 5;
op[5] = 2;
op[3] = 6;
op[6] = 3;
}
public static void main(String[] args) {
init();
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
long conflict[][] = new long[6][6];
for (int i = 0; i < 6; i++) {
for (int j = 0; j < 6; j++) {
conflict[i][j]=1;
}
}
//建立冲突矩阵
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
conflict[op[a] - 1][b - 1] = 0;
conflict[op[b] - 1][a - 1] = 0;
}
// 求冲突矩阵的n-1次方
long[][] mPow_n_1 = mPow(conflict, n - 1);
//累加矩阵的每个元素
long ans = 0;
for (int i = 0; i < 6; i++) {
for (int j = 0; j < 6; j++) {
ans = (ans + mPow_n_1[i][j]) % MOD;
}
}
//ans*4^n
System.out.println(ans * power(4, n) % MOD);
}
private static long power(long i, int n) {
long ans = 1;
while (n != 0) {
if ((n & 1) == 1) ans = (ans * i) % MOD;
i = i * i % MOD;
n >>= 1;
}
return ans;
}
/*矩阵的快速幂*/
private static long[][] mPow(long[][] conflict, int n) {
long[][] e = new long[6][6];
for (int i = 0; i < 6; i++) {
for (int j = 0; j < 6; j++) {
if (i == j) e[i][j] = 1;
else e[i][j] = 0;
}
}
while (n != 0) {
if ((n & 1) == 1) {
e = mMul(e, conflict);
}
conflict = mMul(conflict, conflict);
n >>= 1;
}
return e;
}
private static long[][] mMul(long[][] a, long[][] b) {
long[][] ans = new long[6][6];
for (int i = 0; i < 6; i++) {
for (int j = 0; j < 6; j++) {
for (int k = 0; k < 6; k++) {
ans[i][j] = (ans[i][j] + a[i][k] * b[k][j]) % MOD;
}
}
}
return ans;
}
}
10.生命之树
在X森林里,上帝创建了生命之树。
他给每棵树的每个节点(叶子也称为一个节点)上,都标了一个整数,代表这个点的和谐值。
上帝要在这棵树内选出一个非空节点集S,使得对于S中的任意两个点a,b,都存在一个点列 {a, v1, v2, ..., vk, b} 使得这个点列中的每个点都是S里面的元素,且序列中相邻两个点间有一条边相连。
在这个前提下,上帝要使得S中的点所对应的整数的和尽量大。
这个最大的和就是上帝给生命之树的评分。
经过atm的努力,他已经知道了上帝给每棵树上每个节点上的整数。但是由于 atm 不擅长计算,他不知道怎样有效的求评分。他需要你为他写一个程序来计算一棵树的分数。
「输入格式」
第一行一个整数 n 表示这棵树有 n 个节点。
第二行 n 个整数,依次表示每个节点的评分。
接下来 n-1 行,每行 2 个整数 u, v,表示存在一条 u 到 v 的边。由于这是一棵树,所以是不存在环的。
「输出格式」
输出一行一个数,表示上帝给这棵树的分数。
「样例输入」
5
1 -2 -3 4 5
4 2
3 1
1 2
2 5
「样例输出」
8
「数据范围」
对于 30% 的数据,n <= 10
对于 100% 的数据,0 < n <= 10^5, 每个节点的评分的绝对值不超过 10^6 。
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 3000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
这题正解是树状dp,无根树转有根树,思维难度很大,但是30%数据是10以内的,搜索应该能拿下,原则尽量拿更多的分0.0,暴力解的话,可以枚举所有的子集,再判断所有的子集中是否符合联通,这里的判断可以用dfs搜索或者并查集拿下30%
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
/*
生命之树
在X森林里,上帝创建了生命之树。
他给每棵树的每个节点(叶子也称为一个节点)上,都标了一个整数,代表这个点的和谐值。
上帝要在这棵树内选出一个非空节点集S,使得对于S中的任意两个点a,b,都存在一个点列 {a, v1, v2, ..., vk, b} 使得这个点列中的每个点都是S里面的元素,且序列中相邻两个点间有一条边相连。
在这个前提下,上帝要使得S中的点所对应的整数的和尽量大。
这个最大的和就是上帝给生命之树的评分。
经过atm的努力,他已经知道了上帝给每棵树上每个节点上的整数。但是由于 atm 不擅长计算,他不知道怎样有效的求评分。他需要你为他写一个程序来计算一棵树的分数。
「输入格式」
第一行一个整数 n 表示这棵树有 n 个节点。
第二行 n 个整数,依次表示每个节点的评分。
接下来 n-1 行,每行 2 个整数 u, v,表示存在一条 u 到 v 的边。由于这是一棵树,所以是不存在环的。
「输出格式」
输出一行一个数,表示上帝给这棵树的分数。
「样例输入」
5
1 -2 -3 4 5
4 2
3 1
1 2
2 5
「样例输出」
8
「数据范围」
对于 30% 的数据,n <= 10
对于 100% 的数据,0 < n <= 10^5, 每个节点的评分的绝对值不超过 10^6 。
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 3000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
*/
public class _10生命之树 {
private static int n;
private static long[] w;
private static List[] g;
private static long ans ;
public static void main(String[] args) throws FileNotFoundException {
System.setIn(new FileInputStream(new File("/Users/zhengwei/workspace/lanqiaobei2019/src/2015_Java_B/data10/in5.txt")));
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
w = new long[n + 1];
g = new ArrayList[n + 1];
initG();
for (int i = 1; i <= n; i++) {
w[i] = sc.nextLong();
}
for (int i = 0; i < n - 1; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
g[a].add(b);
g[b].add(a);
}
dfs(1, 0);
System.out.println(ans);
}
/**
* u做为根所代表的子树有一个最大权和,将其存储在w[u]中
* @param u
* @param fa
*/
private static void dfs(int u, int fa) {
for (int i = 0; i < g[u].size(); i++) {
Integer child = g[u].get(i);
if (child == fa) continue;
dfs(child, u);
if (w[child] > 0)
w[u] += w[child];
}
if (w[u] > ans) ans = w[u];
}
private static void initG() {
for (int i = 0; i < n + 1; i++) {
g[i] = new ArrayList();
}
}
}
小结:
01 三角形面积 热身 不用编程
02 立方变自身 简单枚举
03 三羊献瑞 简单枚举 小技巧
*04 循环节长度 有坑 逻辑
05 九数组分数 全排列 带分数
06 加法变乘法 简单枚举 小技巧
07 牌型种数 递归
08 饮料换购 模拟
****09 垒骰子 递归-动规-矩阵快速幂
*****10 生命之树 Java中递归最多1万层