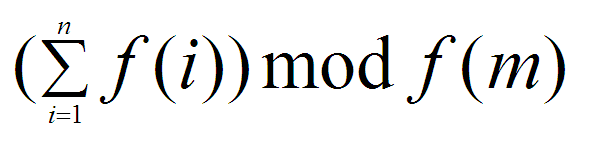2014年第五届蓝桥杯省赛试题及详解(Java本科A组)
蓝桥杯历年真题题目及题解目录汇总
- 结果填空 (满分2分)
- 结果填空 (满分6分)
- 结果填空 (满分7分)
- 代码填空 (满分4分)
- 代码填空 (满分12分)
- 结果填空 (满分12分)
- 结果填空 (满分9分)
- 程序设计(满分8分)
- 程序设计(满分17分)
- 程序设计(满分23分)
1.标题:猜年龄
小明带两个妹妹参加元宵灯会。别人问她们多大了,她们调皮地说:“我们俩的年龄之积是年龄之和的6倍”。小明又补充说:“她们可不是双胞胎,年龄差肯定也不超过8岁啊。”
请你写出:小明的较小的妹妹的年龄。
注意: 只写一个人的年龄数字,请通过浏览器提交答案。不要书写任何多余的内容。
答案:10 2个for
public class _01猜年龄1 {
public static void main(String[] args) {
for(int i=1;i<=100;i++)
for(int j=i;j<=i+8;j++)
if(i*j==6*(i+j))
System.out.println(i+" "+j);
}
}
2.标题:李白打酒
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒2斗。他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店5次,遇到花10次,已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白遇到店和花的次序,可以把遇店记为a,遇花记为b。则:babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢?请你计算出所有可能方案的个数(包含题目给出的)。
注意:通过浏览器提交答案。答案是个整数。不要书写任何多余的内容。
14,读完题目知道要考递归了,理清思路,5(a)次店必须都去,10(b)次花都要遇见,而且结束的时候酒要喝完,最稳的写法就是写3个递归出口,不过发现可以剪枝,3个是不必要的,当一个变量为0就可以进行最后的判断了,严谨的话还要给酒壶是否为空一个判断,不过这里now为负的话,喝酒也不会为正,不可能为答案
public class _02李白打酒1 {
public static void main(String[] args) {
System.out.println(f(5,10,2));
}
static int f(int a,int b,int now) {
if(b==0)
return (a==0&&now==0)?1:0;
if(a==0)
return (b==now)?1:0;
return f(a-1,b,2*now) + f(a,b-1,now-1);
}
}
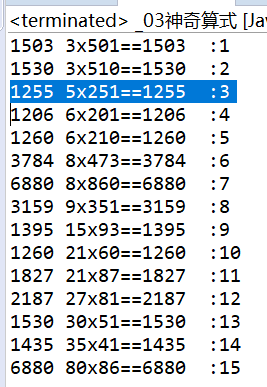
3.标题:神奇算式
由4个不同的数字,组成的一个乘法算式,它们的乘积仍然由这4个数字组成。
比如:
210 x 6 = 1260
8 x 473 = 3784
27 x 81 = 2187
都符合要求。
如果满足乘法交换律的算式算作同一种情况,那么,包含上边已列出的3种情况,一共有多少种满足要求的算式。
请填写该数字,通过浏览器提交答案,不要填写多余内容(例如:列出所有算式)。
答案:12,这题有点恶心org,我的思路是2个for枚举1-999他们乘积,这个乘积先要满足2个条件第一个是它是4位,第二个是它是不同的数字组合,这个可以最后打印肉眼判断,还有i和j加起来长度要为4,最后枚举i和j的全排列找答案
pass:后来发现我的代码中注释了if(flag==1)的筛重,和没注释前对比可以快速找到答案,18-15=3个,意味着有3个有重复数字的答案,不过还是肉眼判断稳
public class _03神奇算式 {
public static void main(String[] args) {
for(i=1;i<1000;i++)
for(j=i+1;j<1000;j++) {
flag=0;
dfs((""+i+j).toCharArray(),0,i*j);
}
}
static int ans=0,flag=0;
static int i,j;
static void dfs(char[] ch,int m,int sum) {
if(ch.length!=4 || sum<1000 || sum>9999)
return;
if(flag==1)
return;
if(m>=4) {
if(ch[0]=='0')
return;
if(Integer.parseInt(new String(ch))==sum) {
ans++;
System.out.println(new String(ch)+" "+i+"x"+j+"=="+sum+" :"+ans);
flag = 1;
}
return;
}
for(int i=m;i<4;i++) {
swap(ch,i,m);
dfs(ch,m+1,sum);
swap(ch,i,m);
}
}
private static void swap(char[] ch, int i, int j) {
char c = ch[i];
ch[i] = ch[j];
ch[j] = c;
}
}
4.标题:写日志
写日志是程序的常见任务。现在要求在 t1.log, t2.log, t3.log 三个文件间轮流写入日志。也就是说第一次写入t1.log,第二次写入t2.log,... 第四次仍然写入t1.log,如此反复。
下面的代码模拟了这种轮流写入不同日志文件的逻辑。
public class A
{
private static int n = 1;
public static void write(String msg)
{
String filename = "t" + n + ".log";
n = ____________;
System.out.println("write to file: " + filename + " " + msg);
}
}请填写划线部分缺失的代码。通过浏览器提交答案。
注意:不要填写题面已有的内容,也不要填写任何说明、解释文字。
1 + n%3 ,求模操作,可以把n=1,2,3代进去验证
5.标题:锦标赛
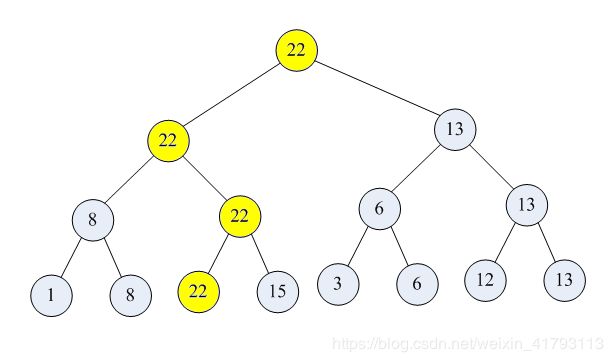
如果要在n个数据中挑选出第一大和第二大的数据(要求输出数据所在位置和值),使用什么方法比较的次数最少?我们可以从体育锦标赛中受到启发。
如图【1.png】所示,8个选手的锦标赛,先两两捉对比拼,淘汰一半。优胜者再两两比拼...直到决出第一名。
第一名输出后,只要对黄色标示的位置重新比赛即可。
下面的代码实现了这个算法(假设数据中没有相同值)。
代码中需要用一个数组来表示图中的树(注意,这是个满二叉树, 不足需要补齐)。它不是存储数据本身,而是存储了数据的下标。
第一个数据输出后,它所在的位置被标识为-1
class A{
//a 表示待处理的数据,长度如果不是2的次幂,则不足位置补为-1
static void pick(int[] a)
{
int n = 1;
while(n0; i-=2){
if(b[i]<0){
if(b[i-1]>=0)
b[(i-1)/2] = b[i-1];
else
b[(i-1)/2] = -1;
}
else{
if(a[b[i]]>a[b[i-1]])
b[(i-1)/2] = b[i];
else
b[(i-1)/2] = b[i-1];
}
}
//输出树根
System.out.println(b[0] + ": " + a[b[0]]);
//值等于根元素的位置需要重新pk
pk(a,b,0,b[0]);
//再次输出树根
System.out.println(b[0] + ": " + a[b[0]]);
}
// a 表示待处理数据,b 二叉树,k 当前要重新比拼的位置,v 已经决胜出的值
static void pk(int[] a, int[] b, int k, int v)
{
int k1 = k*2+1;
int k2 = k1 + 1;
if(k1>=b.length || k2>=b.length){
b[k] = -1;
return;
}
if(b[k1]==v)
pk(a,b,k1,v);
else
pk(a,b,k2,v);
//重新比较
if(b[k1]<0){
if(b[k2]>=0)
b[k] = b[k2];
else
b[k] = -1;
return;
}
if(b[k2]<0){
if(b[k1]>=0)
b[k] = b[k1];
else
b[k] = -1;
return;
}
if(__________________________) //填空
b[k] = b[k1];
else
b[k] = b[k2];
}
}
请仔细分析流程,填写缺失的代码。
通过浏览器提交答案,只填写缺失的代码,不要填写已有代码或其它说明语句等。
答案:a[b[k1]] > a[b[k2]]
胜者树,最大堆原理,有了数据结构知识背景,代码不用很详细的看,谁大赋值成谁,前面都是最大堆的实现代码和边界处理,如果发现题目给的东西没用上,比如a数组,答案很可能出错了
6.标题:六角填数
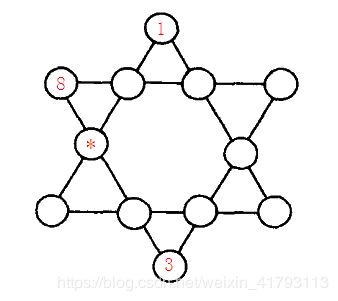
如图【1.png】所示六角形中,填入1~12的数字。
使得每条直线上的数字之和都相同。
图中,已经替你填好了3个数字,请你计算星号位置所代表的数字是多少?
请通过浏览器提交答案,不要填写多余的内容。
还想当生活中的数独做的,不过给的也太少了,先上个暴力全排把
首先要给他们编号,从上到下左到右把,不容易乱,乱了就头疼了
注意,这样写的全排函数初始化一定要有顺序,不然全排个数就不是n!,所以从第一个开始递归,先别固定题目给的1,8,3
把他们作为if条件
public class 六角填数 {
public static void main(String[] args) {
dfs(0);
}
static int[] a = new int[] {1,2,3,4,5,6,7,8,9,10,11,12};//星在下标5
//1,2,3,4 0,2,5,7 7,8,9,10 1,5,8,11 0,3,6,10 4,6,9,11
static void dfs(int m) {
if(m>=12) {
if(a[1]+a[2]+a[3]+a[4] == a[0]+a[2]+a[5]+a[7] && a[1]+a[2]+a[3]+a[4] == a[7]+a[8]+a[9]+a[10]
&& a[1]+a[2]+a[3]+a[4] == a[1]+a[5]+a[8]+a[11] && a[1]+a[2]+a[3]+a[4] == a[0]+a[3]+a[6]+a[10]
&& a[1]+a[2]+a[3]+a[4] == a[4]+a[6]+a[9]+a[11] && a[0]==1 && a[1]==8 && a[11]==3)
System.out.println(a[5]);
return;
}
for(int i=m;i<12;i++) {
swap(i,m);
dfs(m+1);
swap(i,m);
}
}
static void swap(int i,int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
}
7.标题:绳圈
今有 100 根绳子,当然会有 200 个绳头。
如果任意取绳头两两配对,把所有绳头都打结连接起来。最后会形成若干个绳圈(不考虑是否套在一起)。
我们的问题是:请计算最后将形成多少个绳圈的概率最大?
注意:结果是一个整数,请通过浏览器提交该数字。不要填写多余的内容。
3
本题对数学的推理要求比较高,首先我们要分析,现在有n根绳子,那么任意选取其中两个绳头配对,直到所有绳头均已完成配对,有多少种情况呢?
假设n-1根绳子配对完毕共有f(n - 1)种情况,那么在此基础上加一根绳子,重新进行配对,有以下两种情况可以选择:(1)绳圈个数不变,在n - 1根已配对完毕的绳头中选择一个绳头和当前新添加的一根绳子绳头打结连接起来;(2)增加一个绳圈,直接让新添加的绳子两个绳头直接相连。
所以f(n) = f(n - 1) * (C(1, 2*(n - 1))+ C(0, 2*(n - 1))) = f(n - 1) * (2*n - 2 + 1) = f(n - 1) * (2*n - 1)
有了上述公式,那么可以推导出解决本题的动态转移方程,dp[i][j] = dp[i - 1][j] * (2*n - 2) / (2*n - 1) + dp[i - 1][j - 1] * (1) / (2*n - 1)
dp[i][j]表示当前有i根绳子,形成j个绳圈的概率。(PS:j > i,其概率为0)
8.标题:兰顿蚂蚁
兰顿蚂蚁,是于1986年,由克里斯·兰顿提出来的,属于细胞自动机的一种。
平面上的正方形格子被填上黑色或白色。在其中一格正方形内有一只“蚂蚁”。
蚂蚁的头部朝向为:上下左右其中一方。
蚂蚁的移动规则十分简单:
若蚂蚁在黑格,右转90度,将该格改为白格,并向前移一格;
若蚂蚁在白格,左转90度,将该格改为黑格,并向前移一格。
规则虽然简单,蚂蚁的行为却十分复杂。刚刚开始时留下的路线都会有接近对称,像是会重复,但不论起始状态如何,蚂蚁经过漫长的混乱活动后,会开辟出一条规则的“高速公路”。
蚂蚁的路线是很难事先预测的。
你的任务是根据初始状态,用计算机模拟兰顿蚂蚁在第n步行走后所处的位置。
【数据格式】
输入数据的第一行是 m n 两个整数(3 < m, n < 100),表示正方形格子的行数和列数。
接下来是 m 行数据。
每行数据为 n 个被空格分开的数字。0 表示白格,1 表示黑格。
接下来是一行数据:x y s k, 其中x y为整数,表示蚂蚁所在行号和列号(行号从上到下增长,列号从左到右增长,都是从0开始编号)。s 是一个大写字母,表示蚂蚁头的朝向,我们约定:上下左右分别用:UDLR表示。k 表示蚂蚁走的步数。
输出数据为两个空格分开的整数 p q, 分别表示蚂蚁在k步后,所处格子的行号和列号。
例如, 输入:
5 6
0 0 0 0 0 0
0 0 0 0 0 0
0 0 1 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
2 3 L 5
程序应该输出:
1 3
再例如, 输入:
3 3
0 0 0
1 1 1
1 1 1
1 1 U 6
程序应该输出:
0 0
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
前段时间写过:[蓝桥杯][2014年第五届真题]兰顿蚂蚁
和普通的搜索差不多,写dx,dy函数的时候要按顺时针方向了,因为它向左向右,实际上就是顺时针和逆时针,数组有没越界都不用管了,题目根本没提,默认没越界,还见识过 一个 for 4个 if 的暴力做法,很prefer
import java.util.Scanner;
public class 兰顿蚂蚁 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
n = in.nextInt();
m = in.nextInt();
mp = new int[n][m];
for(int i=0;i
9.标题:斐波那契
斐波那契数列大家都非常熟悉。它的定义是:
f(x) = 1 .... (x=1,2)
f(x) = f(x-1) + f(x-2) .... (x>2)
对于给定的整数 n 和 m,我们希望求出:
f(1) + f(2) + ... + f(n) 的值。但这个值可能非常大,所以我们把它对 f(m) 取模。
公式参见【图1.png】
但这个数字依然很大,所以需要再对 p 求模。
【数据格式】
输入为一行用空格分开的整数 n m p (0 < n, m, p < 10^18)
输出为1个整数
例如,如果输入:
2 3 5
程序应该输出:
0
再例如,输入:
15 11 29
程序应该输出:
25
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
Σf(n)=f(n+2)-1 尽量用迭代 规模很大,数据很大 快速斐波那契<--矩阵运算<--快速矩阵幂运算(logn时间复杂度) mod带入到矩阵乘法中,每次乘和每次加,都对结果进行模运算->运算数在LL的范围内 整数快速乘法,并在乘法中加入模运算
/*
标题:斐波那契
斐波那契数列大家都非常熟悉。它的定义是:
f(x) = 1 .... (x=1,2)
f(x) = f(x-1) + f(x-2) .... (x>2)
对于给定的整数 n 和 m,我们希望求出:
f(1) + f(2) + ... + f(n) 的值。但这个值可能非常大,所以我们把它对 f(m) 取模。
公式参见【图1.png】
但这个数字依然很大,所以需要再对 p 求模。
【数据格式】
输入为一行用空格分开的整数 n m p (0 < n, m, p < 10^18)
输出为1个整数
例如,如果输入:
2 3 5
程序应该输出:
0
再例如,输入:
15 11 29
程序应该输出:
25
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
*/
//1.由定义fib(n) = fib(n+2)-fib(n+1)
//2.由1得Σf(n) = f(n+2)-1;
import java.math.BigInteger;
import java.util.Scanner;
//如果 m>=n+2那么f(m)>Σf(n),结果是(f(n+2)-1)%p
//否则 结果为(f(n+2)-1)%f(m)%p==f(n+2)%f(m)%p-1
public class _09_斐波那契 {
public static void main(String[] args) {
// for (int i = 3; i <=10 ; i++) {
// System.out.println(fib(i).longValue());
// }
Scanner sc = new Scanner(System.in);
long n, m, p;
n = sc.nextLong();
m = sc.nextLong();
p = sc.nextLong();
BigInteger bigP = BigInteger.valueOf(p);
if (m >= n + 2) {
BigInteger ans = fib(n + 2, bigP);
System.out.println(ans.mod(bigP).longValue() - 1);
} else {
BigInteger fibm = fib(m);
BigInteger ans = fib(n + 2, fibm);
System.out.println(ans.mod(fibm).mod(bigP).longValue() - 1);
}
}
/*快速矩阵求fib*/
private static BigInteger fib(long m) {
BigInteger[][] ans = mPow(m - 2);
return ans[0][0].add(ans[1][0]);
}
private static BigInteger fib(long m,BigInteger mod) {
BigInteger[][] ans = mPow(m - 2,mod);
return ans[0][0].add(ans[1][0]);
}
/*矩阵快速幂运算*/
private static BigInteger[][] mPow(long n) {
// a 1110
BigInteger[][] a =
{
{
BigInteger.ONE, BigInteger.ONE
},
{
BigInteger.ONE, BigInteger.ZERO
}
};
//单元矩阵
BigInteger[][] ans =
{
{
BigInteger.ONE, BigInteger.ZERO
},
{
BigInteger.ZERO, BigInteger.ONE
}
};
while (n != 0) {
if ((n & 1) == 1) {
//结果ans乘以当前平方
BigInteger t1=ans[0][0];
BigInteger t2=ans[1][0];
ans[0][0] = ans[0][0].multiply(a[0][0]).add(ans[0][1].multiply(a[1][0]));
ans[0][1] = t1.multiply(a[0][1]).add(ans[0][1].multiply(a[1][1]));
ans[1][0] = ans[1][0].multiply(a[0][0]).add(ans[1][1].multiply(a[1][0]));
ans[1][1] = t2.multiply(a[0][1]).add(ans[1][1].multiply(a[1][1]));
}
//对a进行平方
BigInteger t1=a[0][0];
BigInteger t2=a[1][0];
BigInteger t3=a[0][1];
a[0][0] = a[0][0].multiply(a[0][0]).add(a[0][1].multiply(a[1][0]));
a[0][1] = t1.multiply(a[0][1]).add(a[0][1].multiply(a[1][1]));
a[1][0] = a[1][0].multiply(t1).add(a[1][1].multiply(a[1][0]));
a[1][1] = t2.multiply(t3).add(a[1][1].multiply(a[1][1]));
n >>= 1;
}
return ans;
}
private static BigInteger[][] mPow(long n,BigInteger mod) {
BigInteger[][] a =
{
{
BigInteger.ONE, BigInteger.ONE
},
{
BigInteger.ONE, BigInteger.ZERO
}
};
//单元矩阵
BigInteger[][] ans =
{
{
BigInteger.ONE, BigInteger.ZERO
},
{
BigInteger.ZERO, BigInteger.ONE
}
};
while (n != 0) {
if ((n & 1) == 1) {
//结果乘以当前平方
BigInteger t1=ans[0][0];
BigInteger t2=ans[1][0];
ans[0][0] = ans[0][0].multiply(a[0][0]).add(ans[0][1].multiply(a[1][0])).mod(mod);
ans[0][1] = t1.multiply(a[0][1]).add(ans[0][1].multiply(a[1][1])).mod(mod);
ans[1][0] = ans[1][0].multiply(a[0][0]).add(ans[1][1].multiply(a[1][0])).mod(mod);
ans[1][1] = t2.multiply(a[0][1]).add(ans[1][1].multiply(a[1][1])).mod(mod);
}
//进行平方
BigInteger t1=a[0][0];
BigInteger t2=a[1][0];
BigInteger t3=a[0][1];
a[0][0] = a[0][0].multiply(a[0][0]).add(a[0][1].multiply(a[1][0])).mod(mod);
a[0][1] = t1.multiply(a[0][1]).add(a[0][1].multiply(a[1][1])).mod(mod);
a[1][0] = a[1][0].multiply(t1).add(a[1][1].multiply(a[1][0])).mod(mod);
a[1][1] = t2.multiply(t3).add(a[1][1].multiply(a[1][1])).mod(mod);
n >>= 1;
}
return ans;
}
}
10.标题:波动数列
观察这个数列:
1 3 0 2 -1 1 -2 ...
这个数列中后一项总是比前一项增加2或者减少3。
栋栋对这种数列很好奇,他想知道长度为 n 和为 s 而且后一项总是比前一项增加a或者减少b的整数数列可能有多少种呢?
【数据格式】
输入的第一行包含四个整数 n s a b,含义如前面说述。
输出一行,包含一个整数,表示满足条件的方案数。由于这个数很大,请输出方案数除以100000007的余数。
例如,输入:
4 10 2 3
程序应该输出:
2
【样例说明】
这两个数列分别是2 4 1 3和7 4 1 -2。
【数据规模与约定】
对于10%的数据,1<=n<=5,0<=s<=5,1<=a,b<=5;
对于30%的数据,1<=n<=30,0<=s<=30,1<=a,b<=30;
对于50%的数据,1<=n<=50,0<=s<=50,1<=a,b<=50;
对于70%的数据,1<=n<=100,0<=s<=500,1<=a, b<=50;
对于100%的数据,1<=n<=1000,-1,000,000,000<=s<=1,000,000,000,1<=a, b<=1,000,000。
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
import java.util.Scanner;
/*
标题:波动数列
观察这个数列:
1 3 0 2 -1 1 -2 ...
这个数列中后一项总是比前一项增加2或者减少3。
栋栋对这种数列很好奇,他想知道长度为 n 和为 s 而且后一项总是比前一项增加a或者减少b的整数数列可能有多少种呢?
【数据格式】
输入的第一行包含四个整数 n s a b,含义如前面说述。
输出一行,包含一个整数,表示满足条件的方案数。由于这个数很大,请输出方案数除以100000007的余数。
例如,输入:
4 10 2 3
程序应该输出:
2
【样例说明】
这两个数列分别是2 4 1 3和7 4 1 -2。
【数据规模与约定】
对于10%的数据,1<=n<=5,0<=s<=5,1<=a,b<=5;
对于30%的数据,1<=n<=30,0<=s<=30,1<=a,b<=30;
对于50%的数据,1<=n<=50,0<=s<=50,1<=a,b<=50;
对于70%的数据,1<=n<=100,0<=s<=500,1<=a, b<=50;
对于100%的数据,1<=n<=1000,-1,000,000,000<=s<=1,000,000,000,1<=a, b<=1,000,000。
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
*/
public class _10波动数列 {
private static int n;
private static long s;
private static long a;
private static long b;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
s = sc.nextLong();
a = sc.nextLong();
b = sc.nextLong();
int t = n * (n - 1) / 2;
int[] dp = new int[t + 1];
dp[0] = 1;
for (int i = 1; i <= n - 1; i++) {
for (int j = i * (i + 1) / 2; j >= i; j--) {
// dp[j] += dp[j - i];
// if (dp[j] > 100000007) dp[j] %= 100000007;
dp[j] = (dp[j] + dp[j - i]) % 100000007;
}
}
long ans = 0;
for (int i = 0; i <= t; i++) {
if ((s - i * a + (t - i) * b) % n == 0)
ans = (ans + dp[i]) % 100000007;
// if (ans > 100000007) ans %= 100000007;
}
System.out.println(ans);
}
}
小结:
01 猜年龄 简单运算
02 李白打酒 递归
03 神奇算式 枚举,去重复
04 写日志 取余,简单运算
**05 锦标赛 梳理代码逻辑,数组表示树,树的递归
06 六角填数 全排列
***07 绳圈 dp问题
08 兰顿蚂蚁 模拟
****09 斐波那契 1.掌握性质,2.斐波那契的矩阵快速幂解法,3.BigInteger
****10 波动数列 高级dp,01背包