2017年第八届蓝桥杯省赛试题及详解(Java本科A组)
蓝桥杯历年真题题目及题解目录汇总
- 结果填空 (满分5分)
- 结果填空 (满分11分)
- 结果填空 (满分13分)
- 结果填空 (满分17分)
- 代码填空 (满分7分)
- 代码填空 (满分9分)
- 程序设计(满分19分)
- 程序设计(满分21分)
- 程序设计(满分23分)
- 程序设计(满分25分)
1.标题:迷宫
X星球的一处迷宫游乐场建在某个小山坡上。
它是由10x10相互连通的小房间组成的。
房间的地板上写着一个很大的字母。
我们假设玩家是面朝上坡的方向站立,则:
L表示走到左边的房间,
R表示走到右边的房间,
U表示走到上坡方向的房间,
D表示走到下坡方向的房间。
X星球的居民有点懒,不愿意费力思考。
他们更喜欢玩运气类的游戏。这个游戏也是如此!
开始的时候,直升机把100名玩家放入一个个小房间内。
玩家一定要按照地上的字母移动。
迷宫地图如下:
------------
UDDLUULRUL
UURLLLRRRU
RRUURLDLRD
RUDDDDUUUU
URUDLLRRUU
DURLRLDLRL
ULLURLLRDU
RDLULLRDDD
UUDDUDUDLL
ULRDLUURRR
------------
请你计算一下,最后,有多少玩家会走出迷宫?
而不是在里边兜圈子。
请提交该整数,表示走出迷宫的玩家数目,不要填写任何多余的内容。
如果你还没明白游戏规则,可以参看一个简化的4x4迷宫的解说图:
p1.png
“把100名玩家放入一个个小房间内”意思就是每个格子有一个玩家,不然不仔细看题还不知道玩家在哪儿呢qaq
这题很简单,就是对每一个格子作一次搜索,能在有效次数内走去迷宫的就++,因为不在有效次数内说明有循环嘛,当然也可以vis[][]数组标记下重复路径(大材小用),或者换成递归写法传入父亲的坐标(上一个节点),这里用的是迭代,答案:31
相似题:[蓝桥杯][2014年第五届真题]兰顿蚂蚁
public class _01__迷宫 {
public static void main(String[] args) {
int ans=0;
for(int i=0;i<10;i++)
for(int j=0;j<10;j++)
if(ok(i,j))
ans++;
System.out.println(ans);
}
static char[][] ch = new char[][] {
"UDDLUULRUL".toCharArray(),
"UURLLLRRRU".toCharArray(),
"RRUURLDLRD".toCharArray(),
"RUDDDDUUUU".toCharArray(),
"URUDLLRRUU".toCharArray(),
"DURLRLDLRL".toCharArray(),
"ULLURLLRDU".toCharArray(),
"RDLULLRDDD".toCharArray(),
"UUDDUDUDLL".toCharArray(),
"ULRDLUURRR".toCharArray()};
static boolean ok(int x,int y) {
int t=25;
while(t-->0) {
if(x<0 || x>=10 || y<0 || y>=10)
return true;
if(ch[x][y]=='U')
x--;
else if(ch[x][y]=='D')
x++;
else if(ch[x][y]=='L')
y--;
else if(ch[x][y]=='R')
y++;
}
return false;
}
}2.标题:9数算式
观察如下的算式:
9213 x 85674 = 789314562
左边的乘数和被乘数正好用到了1~9的所有数字,每个1次。
而乘积恰好也是用到了1~9的所有数字,并且每个1次。
请你借助计算机的强大计算能力,找出满足如上要求的9数算式一共有多少个?
注意:
1. 总数目包含题目给出的那个示例。
2. 乘数和被乘数交换后作为同一方案来看待。
答案:1625,全排+枚举乘号位置+哈希查重,x*y中不能出现0!!!!!
import java.util.HashSet;
public class _02_9数算式 {
//9213 x 85674 = 789314562 记得ans除2
public static void main(String[] args) {
dfs(0);
System.out.println(ans);
}
static int[] a = new int[] {1,2,3,4,5,6,7,8,9};
static int ans=0;
static HashSet set = new HashSet<>();
static void dfs(int m) {
if(m>=9) {
for(int i=1;i<8;i++) {
int x=0,y=0;
for(int j=0;j=0)
return false;
int[] b = new int[10];
for(int i=0;i 也学习下这个代码思路
import java.util.HashSet;
import java.util.Set;
/*
标题:9数算式
观察如下的算式:
9213 x 85674 = 789314562
左边的乘数和被乘数正好用到了1~9的所有数字,每个1次。
而乘积恰好也是用到了1~9的所有数字,并且每个1次。
请你借助计算机的强大计算能力,找出满足如上要求的9数算式一共有多少个?
注意:
1. 总数目包含题目给出的那个示例。
2. 乘数和被乘数交换后作为同一方案来看待。
请提交一个整数,不要填写任何多余内容或说明文字。
*/
public class _02_9数算式 {
static int[] a = {1, 2, 3, 4, 5, 6, 7, 8, 9};
static int ans;
public static void main(String[] args) {
f(0);
System.out.println(ans/2);
}
private static void f(int k) {
if (k == 9) {
for (int i = 1; i <= 8; i++) {
int x1 = a2i(0, i);
int x2 = a2i(i, 9);
int x = x1 * x2;
if (check(x)) {
ans++;
}
}
}
for (int i = k; i < 9; i++) {
int t = a[k];
a[k] = a[i];
a[i] = t;
f(k + 1);
t = a[k];
a[k] = a[i];
a[i] = t;
}
}
private static boolean check(int x) {
String s = x + "";
if (s.length() != 9||s.indexOf('0')>-1) return false;
Set set = new HashSet();
for (int i = 0; i < s.length(); i++) {
set.add(s.charAt(i));
}
return set.size() == 9;
}
private static int a2i(int i, int j) {
int ans = 0;
int p = 1;
for (int k = j - 1; k >= i; k--) {
ans += a[k] * p;
p *= 10;
}
return ans;
}
}
3.标题:魔方状态
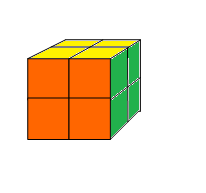
二阶魔方就是只有2层的魔方,只由8个小块组成。
如图p1.png所示。
小明很淘气,他只喜欢3种颜色,所有把家里的二阶魔方重新涂了颜色,如下:
前面:橙色
右面:绿色
上面:黄色
左面:绿色
下面:橙色
后面:黄色
请你计算一下,这样的魔方被打乱后,一共有多少种不同的状态。
如果两个状态经过魔方的整体旋转后,各个面的颜色都一致,则认为是同一状态。
这题有点恶心,把8个块记录为一个数组,每个块有6个面,所以块也是个数组,所以开个二维数组模拟,每次操作有3种,向前顺时针,向上顺时针 ,向左顺时针,hhha,看的有点迷惑了把,不知道大家有没发现玩魔方的大佬玩魔方的时候,只对一个角只往3个方向旋转呢,没错,我们就用bfs记录下所有的状态,大概的思路是这样的= =
import java.util.HashSet;
import java.util.Set;
/*
标题:魔方状态
二阶魔方就是只有2层的魔方,只由8个小块组成。
如图p1.png所示。
小明很淘气,他只喜欢3种颜色,所有把家里的二阶魔方重新涂了颜色,如下:
前面:橙色
右面:绿色
上面:黄色
左面:绿色
下面:橙色
后面:黄色
请你计算一下,这样的魔方被打乱后,一共有多少种不同的状态。
如果两个状态经过魔方的整体旋转后,各个面的颜色都一致,则认为是同一状态。
请提交表示状态数的整数,不要填写任何多余内容或说明文字。
*/
public class _03魔方状态 {
static char[][] start = {"oybbgb".toCharArray(),
"oygbbb".toCharArray(),
"bygbby".toCharArray(),
"bybbgy".toCharArray(),
"obbogb".toCharArray(),
"obgobb".toCharArray(),
"bbgoby".toCharArray(),
"bbbogy".toCharArray()};
static char[][][] q = new char[2000000][8][6];
static Set all_state = new HashSet();
static int front, tail;
static String to_string(char[][] a) {
String ans = "";
for (int i = 0; i < 8; ++i) {
ans += new String(a[i]);
}
return ans;
}
private static void swap(char[] a, int i, int j) {
char t = a[i];
a[i] = a[j];
a[j] = t;
}
private static void swap(char[][] a, int i, int j) {
char[] t = a[i];
a[i] = a[j];
a[j] = t;
}
//上层的块的旋转,面的相对位置调换
static void ucell(char[] a) {
swap(a, 0, 2);
swap(a, 2, 5);
swap(a, 5, 4);
}
//上层顺时针旋转
static void u(char[][] s) {
ucell(s[0]);
ucell(s[1]);
ucell(s[2]);
ucell(s[3]);
// 块的相对位置调换
swap(s, 1, 0);
swap(s, 2, 1);
swap(s, 3, 2);
}
//右层旋转是面的位置变化
static void rcell(char[] a) {
swap(a, 1, 0);
swap(a, 0, 3);
swap(a, 3, 5);
}
static void r(char[][] s)//魔方右层顺时针转
{
rcell(s[1]);
rcell(s[2]);
rcell(s[6]);
rcell(s[5]);
// 块的位置变化
swap(s, 2, 1);
swap(s, 5, 1);
swap(s, 6, 5);
}
static void fcell(char[] a) {
swap(a, 2, 1);
swap(a, 1, 4);
swap(a, 4, 3);
}
static void f(char[][] s)//前面一层 顺时针转
{
fcell(s[0]);
fcell(s[1]);
fcell(s[4]);
fcell(s[5]);
swap(s, 1, 5);
swap(s, 0, 1);
swap(s, 4, 0);
}
static void uwhole(char[][] s)//整个魔方从顶部看 顺时针转 用于判重
{
u(s);//上层旋转
// 下层旋转
ucell(s[4]);
ucell(s[5]);
ucell(s[6]);
ucell(s[7]);
// 完成自旋后,块的位置变动
swap(s, 5, 4);
swap(s, 6, 5);
swap(s, 7, 6);
}
static void fwhole(char[][] s)//整个魔方从前面看 顺时针转 用于判重
{
f(s);
fcell(s[2]);
fcell(s[6]);
fcell(s[7]);
fcell(s[3]);
swap(s, 2, 6);
swap(s, 3, 2);
swap(s, 7, 3);
}
static void rwhole(char[][] s)//整个魔方从右边看 顺时针转 用于判重
{
r(s);
rcell(s[0]);
rcell(s[3]);
rcell(s[4]);
rcell(s[7]);
swap(s, 3, 7);
swap(s, 0, 3);
swap(s, 4, 0);
}
static boolean try_insert(char[][] s) {
char[][] k = new char[8][6];
memcpy(k, s);
for (int i = 0; i < 4; i++) {
fwhole(k);
for (int j = 0; j < 4; j++) {
uwhole(k);
for (int q = 0; q < 4; q++) {
rwhole(k);
if (all_state.contains(to_string(k))) {
return false;
}
}
}
}
all_state.add(to_string(k));
return true;
}
private static void memcpy(char[][] k, char[][] s) {
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 6; j++) {
k[i][j] = s[i][j];
}
}
}
static void solve() {
front = 0;
tail = 1;
all_state.add(to_string(start));
memcpy(q[front], start);//填充q[0],相当于第一个状态入队列
while (front < tail) {
/*将其所有变形,尝试加入set中*/
memcpy(q[tail], q[front]);//拷贝到tail
u(q[tail]);//上层顺时针旋转
if (try_insert(q[tail])) {
tail++;//扩展队列
}
memcpy(q[tail], q[front]);//拷贝到tail
r(q[tail]);//右层顺时针旋转
if (try_insert(q[tail])) {
tail++;//扩展队列
}
memcpy(q[tail], q[front]);//拷贝到tail
f(q[tail]);//前顺时针旋转
if (try_insert(q[tail])) {
tail++;//扩展队列
}
front++;//弹出队首
// cout << front << " " << tail << endl;
}
System.out.println(front);
}
public static void main(String[] args) {
solve();
}
}
4.标题:方格分割
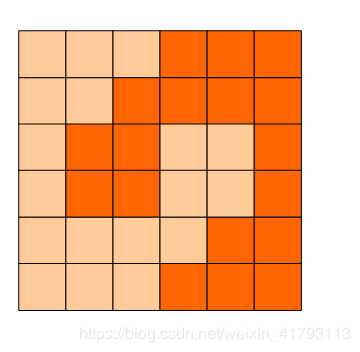
6x6的方格,沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
如图:p1.png, p2.png, p3.png 就是可行的分割法。
试计算:
包括这3种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。
先贴个超时代码典范,按照往年真题剪邮票枚举+求联通快的做法,超时了,2^18次方太多了,而且求出的答案也不一定正确,
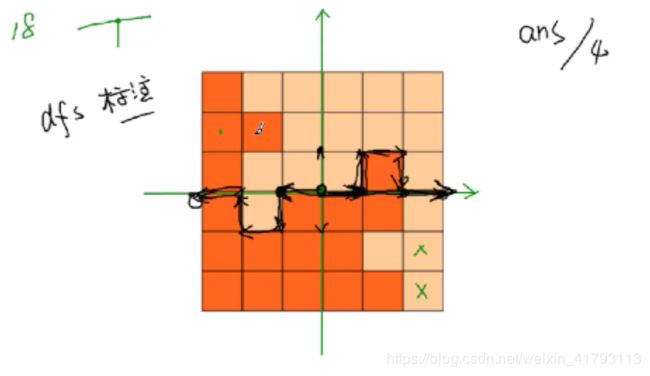
基本的思路是对的,对称位置上的颜色不能一样,即vis[i][j]!=vis[5-i][5-j],在此思路上,我们不妨从搜索块的思路上变成枚举分割线,从中心搜索到边界的线,当然是从2个方向搜索的,不过其实只要搜索一个方向,另外个方向取对称点,对称分割
最后答案别忘了除4(对称),509
public class _04_方格分割 {
public static void main(String[] args) {
dfs(0);
System.out.println(ans);
}
static int[] a = new int[18];// {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35};
static boolean[][] vis = new boolean[6][6];
static int res=0,ans=0;
static int[] dx = new int[] {1,0,-1,0};
static int[] dy = new int[] {0,1,0,-1};
static void dfs(int m) {
for(a[0]=0;a[0]<36;a[0]++)
for(a[1]=a[0]+1;a[1]<36;a[1]++)
for(a[2]=a[1]+1;a[2]<36;a[2]++)
for(a[3]=a[2]+1;a[3]<36;a[3]++)
for(a[4]=a[3]+1;a[4]<36;a[4]++)
for(a[5]=a[4]+1;a[5]<36;a[5]++)
for(a[6]=a[5]+1;a[6]<36;a[6]++)
for(a[7]=a[6]+1;a[7]<36;a[7]++)
for(a[8]=a[7]+1;a[8]<36;a[8]++)
for(a[9]=a[8]+1;a[9]<36;a[9]++)
for(a[10]=a[9]+1;a[10]<36;a[10]++)
for(a[11]=a[10]+1;a[11]<36;a[11]++)
for(a[12]=a[11]+1;a[12]<36;a[12]++)
for(a[13]=a[12]+1;a[13]<36;a[13]++)
for(a[14]=a[13]+1;a[14]<36;a[14]++)
for(a[15]=a[14]+1;a[15]<36;a[15]++)
for(a[16]=a[15]+1;a[16]<36;a[16]++)
for(a[17]=a[16]+1;a[17]<36;a[17]++)
{
for(int i=0;i<6;i++)
for(int j=0;j<6;j++)
vis[i][j] = false;
for(int i=0;i<18;i++)
vis[a[i]/6][a[i]%6] = true;
ok();
}
}
static void ok() {
if(vis[0][0]==false)
return;
for(int i=0;i<6;i++)
for(int j=0;j<6;j++)
if(vis[i][j]==vis[5-i][5-j])
return;
res=0;
for(int i=0;i<6;i++)
for(int j=0;j<6;j++) {
if(vis[i][j]) {
dfs(i,j);
if(res==18) {
ans++;
// System.out.println(ans);
}
return;
}
}
}
static void dfs(int x,int y) {
res++;
vis[x][y] = false;
for(int i=0;i<4;i++) {
int u = x + dx[i];
int v = y + dy[i];
if(u>=0 && u<6 && v>=0 && v<6 && vis[u][v])
dfs(u,v);
}
}
}
AC代码,对称分割,这题考察思维的转化,从关注点是格子转化为点,从而对称的搜索从答案
public class _04_方格分割_对称分割 {
public static void main(String[] args) {
vis[3][3]=true;
dfs(3,3);
System.out.println(ans/4);//别忘了除4~
}
static boolean[][] vis = new boolean[7][7];
static int[] dx = new int[] {1,0,-1,0};
static int[] dy = new int[] {0,1,0,-1};
static int ans = 0;
static void dfs(int x,int y) {
if(x==0 || y==0 || x==6 || y==6) {
ans++;
return;
}
for(int i=0;i<4;i++) {
int u = x+dx[i];
int v = y+dy[i];
if(!vis[u][v]) {
vis[u][v]=vis[6-u][6-v]=true;
dfs(u,v);
vis[u][v]=vis[6-u][6-v]=false;
}
}
}
}
5.标题:字母组串
由 A,B,C 这3个字母就可以组成许多串。
比如:"A","AB","ABC","ABA","AACBB" ....
现在,小明正在思考一个问题:
如果每个字母的个数有限定,能组成多少个已知长度的串呢?
他请好朋友来帮忙,很快得到了代码,
解决方案超级简单,然而最重要的部分却语焉不详。
请仔细分析源码,填写划线部分缺少的内容。
public class A
{
// a个A,b个B,c个C 字母,能组成多少个不同的长度为n的串。
static int f(int a, int b, int c, int n)
{
if(a<0 || b<0 || c<0) return 0;
if(n==0) return 1;
return ________________________________; //填空
}
public static void main(String[] args)
{
System.out.println(f(1,1,1,2));
System.out.println(f(1,2,3,3));
}
}对于上面的测试数据,小明口算的结果应该是:
6
19
注意:只填写划线部分缺少的代码,不要提交任何多余内容或说明性文字。
答案:f(a-1,b,c,n-1)+f(a,b-1,c,n-1)+f(a,b,c-1,n-1),这题观察下出口就知道怎么写了,对递归熟悉的话,很快想出来,这里可以对自己提几个问题,为什么abc最后会小于0,为什么n最后会慢慢变成0,嗯~思路就是这样出来的
6.标题:最大公共子串
最大公共子串长度问题就是:
求两个串的所有子串中能够匹配上的最大长度是多少。
比如:"abcdkkk" 和 "baabcdadabc",
可以找到的最长的公共子串是"abcd",所以最大公共子串长度为4。
下面的程序是采用矩阵法进行求解的,这对串的规模不大的情况还是比较有效的解法。
请分析该解法的思路,并补全划线部分缺失的代码。
public class Main
{
static int f(String s1, String s2)
{
char[] c1 = s1.toCharArray();
char[] c2 = s2.toCharArray();
int[][] a = new int[c1.length+1][c2.length+1];
int max = 0;
for(int i=1; i max) max = a[i][j];
}
}
}
return max;
}
public static void main(String[] args){
int n = f("abcdkkk", "baabcdadabc");
System.out.println(n);
}
}
注意:只提交缺少的代码,不要提交已有的代码和符号。也不要提交说明性文字。
答案:1+a[i-1][j-1],建议粗心党遇到再熟悉的题目也要放进运行控制台验算下
7.描述:正则问题
考虑一种简单的正则表达式:
只由 x ( ) | 组成的正则表达式。
小明想求出这个正则表达式能接受的最长字符串的长度。
例如 ((xx|xxx)x|(x|xx))xx 能接受的最长字符串是: xxxxxx,长度是6。
输入
----
一个由x()|组成的正则表达式。输入长度不超过100,保证合法。
输出
----
这个正则表达式能接受的最长字符串的长度。
例如,
输入:
((xx|xxx)x|(x|xx))xx
程序应该输出:
6
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
不要使用package语句。不要使用jdk1.7及以上版本的特性。
主类的名字必须是:Main,否则按无效代码处理。
这题的题目真的是没有讲明白,xx|xxx其中"|"是左右取最大的值,答案为3,括号就是优先级,递归可以实现这个计算,这里的细节要注意,p++为什么写4个,不只在while块的最后写一个就好,注意return!!!!
import java.util.Scanner;
public class 正则问题 {
//((xx|xxx)x|(x|xx))xx 6
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
s = in.next();
n = s.length();
System.out.println(f());
}
static String s;
static int p=0;//记录指针
static int n=0;//记录长度
static int f() {
int ans=0,temp=0;
while(p
8.标题:包子凑数
小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买X个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼,分别能放3、4和5个包子。当顾客想买11个包子时,大叔就会选2笼3个的再加1笼5个的(也可能选出1笼3个的再加2笼4个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼,分别能放4、5和6个包子。而顾客想买7个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。
输入
----
第一行包含一个整数N。(1 <= N <= 100)
以下N行每行包含一个整数Ai。(1 <= Ai <= 100)
输出
----
一个整数代表答案。如果凑不出的数目有无限多个,输出INF。
例如,
输入:
2
4
5
程序应该输出:
6
再例如,
输入:
2
4
6
程序应该输出:
INF
样例解释:
对于样例1,凑不出的数目包括:1, 2, 3, 6, 7, 11。
对于样例2,所有奇数都凑不出来,所以有无限多个。
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
不要使用package语句。不要使用jdk1.7及以上版本的特性。
主类的名字必须是:Main,否则按无效代码处理。
提交程序时,注意选择所期望的语言类型和编译器类型。
蓝桥杯 历届试题 包子凑数 完全背包dp+扩展欧几里得
import java.util.Scanner;
public class 蓝桥杯_包子凑数 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] a = new int[n+5];
int[] dp = new int[10005];//只有2个数时,最大不能组合的数x*y-x-y,有这个公式
int ans=0;
dp[0]=1;
for(int i=1;i<=n;i++)
a[i] = in.nextInt();
int g = a[1];
for(int i=2;i<=n;i++)
g = gcd(g,a[i]);
if(g!=1) {
System.out.println("INF");
return;
}
for(int i=1;i<=n;i++)
for(int j=a[i];j<=10000;j++)
dp[j] = Math.max(dp[j], dp[j-a[i]]);
for(int j=1;j<=10000;j++)
if(dp[j]==0)
ans++;
System.out.println(ans);
}
static int gcd(int a,int b) {
return b==0?a:gcd(b,a%b);
}
}
9.标题: 分巧克力
儿童节那天有K位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有N块巧克力,其中第i块是Hi x Wi的方格组成的长方形。
为了公平起见,小明需要从这 N 块巧克力中切出K块巧克力分给小朋友们。切出的巧克力需要满足:
1. 形状是正方形,边长是整数
2. 大小相同
例如一块6x5的巧克力可以切出6块2x2的巧克力或者2块3x3的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小Hi计算出最大的边长是多少么?
输入
第一行包含两个整数N和K。(1 <= N, K <= 100000)
以下N行每行包含两个整数Hi和Wi。(1 <= Hi, Wi <= 100000)
输入保证每位小朋友至少能获得一块1x1的巧克力。
输出
输出切出的正方形巧克力最大可能的边长。
样例输入:
2 10
6 5
5 6
样例输出:
2
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
不要使用package语句。不要使用jdk1.7及以上版本的特性。
主类的名字必须是:Main,否则按无效代码处理。
原题链接
提供大家一个oj链接,官网的java过不了,数据出的不好,这里可以AC,思路二分答案
二分答案最后输出的边界很重要,不然很容易WA,下面类似模板结果,ok()函数要自己写
while(l<=r) {
int mid = l + (r-l)/2;
if(ok(mid)) {
l=mid+1;
ans=mid;
}else
r = mid - 1;
}
System.out.println(ans);详细AC代码讲解:蓝桥杯 2017年第八届真题 分巧克力 经典的二分答案 输入挂
10.标题:油漆面积
X星球的一批考古机器人正在一片废墟上考古。
该区域的地面坚硬如石、平整如镜。
管理人员为方便,建立了标准的直角坐标系。
每个机器人都各有特长、身怀绝技。它们感兴趣的内容也不相同。
经过各种测量,每个机器人都会报告一个或多个矩形区域,作为优先考古的区域。
矩形的表示格式为(x1,y1,x2,y2),代表矩形的两个对角点坐标。
为了醒目,总部要求对所有机器人选中的矩形区域涂黄色油漆。
小明并不需要当油漆工,只是他需要计算一下,一共要耗费多少油漆。
其实这也不难,只要算出所有矩形覆盖的区域一共有多大面积就可以了。
注意,各个矩形间可能重叠。
本题的输入为若干矩形,要求输出其覆盖的总面积。
输入格式:
第一行,一个整数n,表示有多少个矩形(1<=n<10000)
接下来的n行,每行有4个整数x1 y1 x2 y2,空格分开,表示矩形的两个对角顶点坐标。
(0<= x1,y1,x2,y2 <=10000)
输出格式:
一行一个整数,表示矩形覆盖的总面积。
例如,
输入:
3
1 5 10 10
3 1 20 20
2 7 15 17
程序应该输出:
340
再例如,
输入:
3
5 2 10 6
2 7 12 10
8 1 15 15
程序应该输出:
128
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
不要使用package语句。不要使用jdk1.7及以上版本的特性。
主类的名字必须是:Main,否则按无效代码处理。
暴力代码,据说当年直接AC哦,不需要线段树+扫描线+离散化
下面的暴力代码确实没有超时,不过官网自己给的第一个测试用例就是错的,呵呵,已经无力吐槽
import java.util.Scanner;
public class 油漆面积 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
vis = new boolean[10005][10005];
// for(int i=0;i<10005;i++)
// for(int j=0;j<10005;j++)
// vis[i][j] = false;
while(n-->0) {
int x1 = in.nextInt();
int y1 = in.nextInt();
int x2 = in.nextInt();
int y2 = in.nextInt();
// if(x1>x2 && y1>y2)
// paint(x2,y2,x1,y1);
// else
paint(x1,y1,x2,y2);
}
int ans=0;
for(int i=0;i<10005;i++)
for(int j=0;j<10005;j++)
if(vis[i][j])
ans++;
System.out.println(ans);
}
static boolean[][] vis;
static void paint(int x1,int y1,int x2,int y2) {
for(int i=x1;i
线段树+扫描线+离散化AC代码,不过官网还是不能AC哦
import java.util.Arrays;
import java.util.Scanner;
/*
标题:油漆面积
X星球的一批考古机器人正在一片废墟上考古。
该区域的地面坚硬如石、平整如镜。
管理人员为方便,建立了标准的直角坐标系。
每个机器人都各有特长、身怀绝技。它们感兴趣的内容也不相同。
经过各种测量,每个机器人都会报告一个或多个矩形区域,作为优先考古的区域。
矩形的表示格式为(x1,y1,x2,y2),代表矩形的两个对角点坐标。
为了醒目,总部要求对所有机器人选中的矩形区域涂黄色油漆。
小明并不需要当油漆工,只是他需要计算一下,一共要耗费多少油漆。
其实这也不难,只要算出所有矩形覆盖的区域一共有多大面积就可以了。
注意,各个矩形间可能重叠。
本题的输入为若干矩形,要求输出其覆盖的总面积。
输入格式:
第一行,一个整数n,表示有多少个矩形(1<=n<10000)
接下来的n行,每行有4个整数x1 y1 x2 y2,空格分开,表示矩形的两个对角顶点坐标。
(0<= x1,y1,x2,y2 <=10000)
输出格式:
一行一个整数,表示矩形面积。
例如,
输入:
3
1 5 10 10
3 1 20 20
2 7 15 17
程序应该输出:
340
再例如,
输入:
3
5 2 10 6
2 7 12 10
8 1 15 15
程序应该输出:
128
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
不要使用package语句。不要使用jdk1.7及以上版本的特性。
主类的名字必须是:Main,否则按无效代码处理。
*/
public class _10油漆面积_2 {
/*辅助的数据结构:扫描线*/
private static class Line implements Comparable {
int x1, x2, h, f;//左右坐标,纵坐标(高度),f=1为入边,f=-1为出边
Line() {
}
Line(int _l, int _r, int _h, int _f) {
x1 = _l;
x2 = _r;
h = _h;
f = _f;
}
/*按高度排序*/
@Override
public int compareTo(Line o) {
if (h < o.h) return -1;
else if (h > o.h) return 1;
else return 0;
}
}
/*线段树的定义*/
private static class SegTree {
int pl, pr, cnt, len;//左端点编号,右端点编号,被覆盖次数,两个端点之间被覆盖的长度
SegTree() {
}
SegTree lson, rson;
}
static int n;
static int[] X ;//= new int[N << 1];//记录所有的横坐标
//int PL=0,PR;
static Line[] lines ;//= new Line[N];
/*构建区间树*/
static SegTree buildTree(int pl, int pr) {
SegTree t = new SegTree();
t.pl = pl;
t.pr = pr;
if (pl == pr) return t;
int mid = ((pl + pr) >> 1);
t.lson = buildTree(pl, mid);
t.rson = buildTree(mid + 1, pr);
return t;
}
static void updateLength(SegTree pTree, int tl, int tr) {
if (pTree.cnt > 0) {
pTree.len = X[tr] - X[tl - 1];//将区间树上的端点(序号)反入到X中求得二维坐标上的实际横坐标
} else if (tl == tr) {
pTree.len = 0;
} else {//负数
pTree.len = pTree.lson.len + pTree.rson.len;
}
}
static void update(SegTree tree, int pl, int pr, int value) {
int tl = tree.pl;
int tr = tree.pr;
if (pl <= tl && pr >= tr) {
tree.cnt += value;
updateLength(tree, tl, tr);
return;
}
int m = (tl + tr) >> 1;
if (pl <= m) update(tree.lson, pl, pr, value);
if (pr > m) update(tree.rson, pl, pr, value);
updateLength(tree, tl, tr);
}
static int ans;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
X=new int[n*2];
lines=new Line[n*2];
int x1, y1, x2, y2;
int index = 0;
for (int i = 0; i < n; i++) {
x1 = sc.nextInt();
y1 = sc.nextInt();
x2 = sc.nextInt();
y2 = sc.nextInt();
X[index] = x1;
lines[index] = new Line(x1, x2, y1, 1);//高度1
index++;
X[index] = x2;
lines[index] = new Line(x1, x2, y2, -1);//高度2
index++;
}
// 大体上就有了2n个横坐标,2n条水平线段
Arrays.sort(X);//所有横坐标点排序
Arrays.sort(lines);//扫描线排序,从低到高
/*离散化横坐标*/
int X_end = unique(X);//去重返回值是一个迭代器,它指向的是去重后容器中不重复序列的最后一个元素
// PR=X_end;
// 初始化线段树
SegTree root = buildTree(1, X_end);
// 从低到高,遍历扫描线
for (int i = 0; i < index-1; ++i) {
int pl = Arrays.binarySearch(X, 0, X_end + 1, lines[i].x1);//二分查找,记录下标,代表是第几个点
int pr = Arrays.binarySearch(X, 0, X_end + 1, lines[i].x2);//二分查找,记录下标,代表是第几个点
update(root, pl + 1, pr, lines[i].f);
ans += root.len * (lines[i + 1].h - lines[i].h);//宽度*高度
}
System.out.println(ans);
}
private static int unique(int[] x) {
int index = 0;
for (int i = 1; i < x.length; i++) {
if (x[i] == x[index]) continue;
else {
index++;
x[index] = x[i];
}
}
return index;
}
}