图像修复：PatchMatch与Space-Time completion

据说Adobe ps cs5 中的基于图像的填充是使用的PatchMatch 和 Space-Time Completion， 最近特意看了一下这两篇paper,然后按照paper所述撸下来，感觉还挺有意思的。

PatchMatch

PatchMatch 算法就是一个找近似最近邻（Approximate Nearest neigbhor)的方法，是一片09年的paper,相较于之前的找ANN的算法速度上快了10+倍。
PatchMatch 的核心思想是利用图像的连续性（consistence）， 一个图像patch块A附近的Patch快的最近邻最有可能出现在Patch快A的最近邻附近，利用这种图像的连续性大量减少搜索的范围，通过迭代的方式保证大多数点能尽快收敛。

对于图A，在图B中寻找每个patch块的最近邻PatchMatch算法步骤如下:

1. 先随机给图A中的每个patch设定一个随机的图B中的patch作为其初始的最近邻patch。其中自然有一些匹配得还可以，一些匹配得不行的。
2. 对于图A中的每个patch块，寻找其周围其他patch块的最近邻所对应位置的patch块作为其候选最近邻（传递附近patch快的最近邻信息），如果距离比当前最近邻小，则进行更新。
3. 为了避免陷入局部极值，再额外再随机生成几个patch位置作为候选最近邻，弱小于当前最近邻，则更新。
4. 多次迭代，奇数次向右向下传递，偶数次向左向上传递。

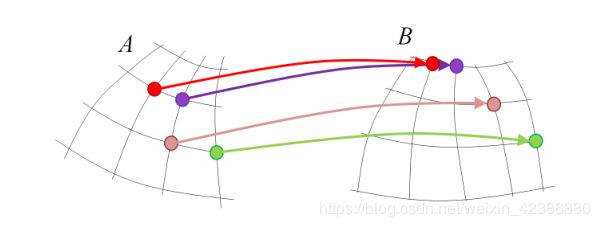
这是一种利用图像连续性的方法，每当找到自己的最近邻的时候，还能将该对应信息传递给周围的patch块，从而达到加速收敛的目的。如下途中，红色Patch找到自己最近邻的情况下，将相应附近的点patch也传递给自己附近的patch块。

Space-Time Completion

这篇paper的目的在于利用一个全局性的目标函数求全局最优来完成图像的填充。发现这篇paper和nonlocal mean denoise有一些异曲同工之妙,都有一种利用点周围patch进行投票的思想，迭代过程都比较优美。
下面简单翻译一下原文吧，感觉说得也不是特别清晰。
按照paper中所说，最完美的填充情况下，图像中需要达到最大的一致性。对于一个视频序列$S$和序列$D$，如果其中每一个时间空间点都能在序列$D$中找到，则认为他们又全局的视角一致性。也就是说用$D$中的窗口来填充$S$中的数据。从$D$中找到的patch块用$V$来表示。$H$则是$S$中的一个需要填充的孔洞区域。我们希望能用一些新的$H^{\ast }$填充丢失区H,得到一个新的和数据D有最高的全局视觉一致性的视频序列$S^{\ast }$。
$$Coherence(S^{\ast }|D)=\prod _{p\in S^{\ast }}{\max }_{q\in D}sim(W_p,V_q)$$
目前没有较好的办法能直接对这个目标函数求解，但是可以知道在最优解的位置，必然满足以下两个条件

1. 包含p点的所有的patch块$W_p^1\dots W_p^k$，都是来自原始的数据$D$
2. 这些patch快在p点的投票值都是一样的，
   $$c=V_i(p)=V^j(p)$$

迭代过程

令$ p \in H$ 属于我们需要提升的某个点，令$W_p^1\dots W_p^k$是所有包含点p的空间时间patch快。令$V_p^1\dots V_p^k$表示与$W_p^1\dots W_p^k$
最相似的patch块。他们越相似，可靠性就越高。
我们需要在点p处选择一个颜色值使得所有包含他的窗口的一致性值提升。所以最有可能的值应该最小化根据$V_p^1\dots V_p^k$所对应值的方差。也就是最小化${\sum }_i{w}_p^i(c-c^i{)}^2$,也就有
$$c=\frac{{\sum }_i{w}_p^i{c}^i}{{\sum }_i{w}_p^i}$$

其他的一些细节

相似度引入梯度

这篇paper中讲了一下只用rgb可能不够，额外加了两维的梯度的数据构成5D数据来评估patch快之间的相似度，我实验对于图像inpainting直接用RGB效果也还可以，可能对于视频的填充更为重要。

权重计算

其中$w_p^i={\alpha }_p^i\cdot s_p^i$, ${\alpha }_p^i$是一个和点到mask边界距离有关的固定的系数值，首先计算Mask图像的距离变换，然后取$\alpha =1.3^{-dist}$ 作为patch块的固定系数，表明该patch块的权重，离已知图像越近，其权重越高。 $s=e^{-\frac{d(W_p,V_p)}{2{\sigma }^2}}$. $\sigma$权重取得是包含p点的所有窗口的距离d的75分位数，作者说这样可以加快收敛。

MeanShift

从上面的递归方式是一种计算各个patch快的加权均值的方式，如果其中有一个点偏离实际值比较远，会导致最终数据出现比较大的偏移，算法收敛速度变慢。
所有作者推荐使用Meanshift来计算最终p点处的color值。

多尺度

通过先在粗尺度上进行处理，再不断进行传播到细尺度上，可以节省大量时间，但是作者没提到的是多尺度有利于算法找到一个较好的初始值，得到更快的收敛效果。

和之前的基于顺序的对比效果

即使对于一些比较复杂的周期性图案，该算法可以较好的处理好

1. 基于边缘优先级的填充算法: 效果非常差，迭代次数很多。为了压缩gif大小，填充50次保留1帧。
   
2. space -time completion：效果可以接受。可以看到图像随着尺度变化，填充的细节也越来越清晰。
   |

缺陷

对于初始化比较敏感，容易陷入局部极值。

还没有说清楚的，可以参考我写的代码，已经上传到github了，如有错误，还请指正。
https://github.com/chwahaha/Space-Time-completion-of-Image

refrence

[1] PatchMatch: A Randomized Correspondence Algorithm for Structural Image Editing
[2]Space-Time completion of Image