Python统计分析(3)——几种重要的概率分布:二项式分布
二项式分布
二项式分布就是只有两个可能结果的分布,比如成功或失败,抛一枚硬币的正反面, 两个可能结果的概率可以相等,也可以是不相等的,总和为1,例如如果成功的概率为0.2,那么失败的概率就是P=1-0.2=0.8. 每一次尝试都是独立的,因为前一次投掷的结果不能影响当前投掷的结果,只有两种可能结果且重复n次的试验叫做二项式,二项式的参数是 n和P,n是试验的总次数,P是试验的概率。
在上述说明的基础上,二项式的属性包括: 1.每个试验都是独立的。 2.实验中只有两个可能的结果:成功和失败。 3.总共进行了相同地n次实验。 4.所有实验成功和失败的概率是相同的。(所有实验都是相同的)
公式:(写本上吧,太复杂打不出来)
PMF (概率质量函数)对离散随机变量的定义,是离散随机变量在各个特定取值的概率。该函数通俗来说,就是对一个离散型概率事件来说,使用该函数来求它各个成功事件结果的概率。 PDF (概率密度函数) 是对连续型随机变量的定义,与PMF不同的是,在特定点上的值并不是该点的概率,连续随机概率事件只能求连续一段区域内发生事件的概率,通过对这段区间进行积分,可获得事件发生时间落在给定间隔内的概率。
#二项式分布——画图
#导入需要的包
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML
#PLOTTING CONFIG 绘图配置
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams['figure.figsize']=(14,7)
plt.figure(dpi=100)
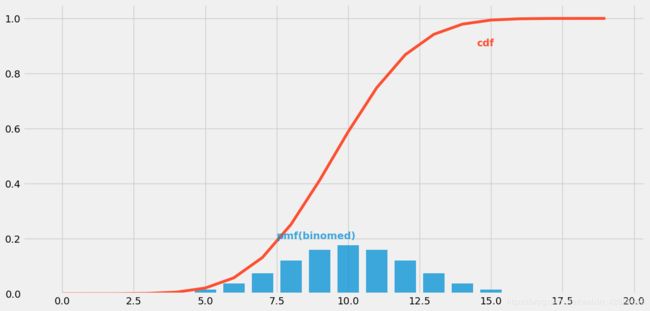
#PMF 绘制概率质量函数
plt.bar(left=(np.arange(20)),height=(stats.binom.pmf(np.arange(20),p=0.5,n=20)),width=0.75,alpha=0.75) #binom.pmf为二项式的概率质量数
#n=20,P=0.5,绘制成柱形图
#CDF
plt.plot(np.arange(20),stats.binom.cdf(np.arange(20),p=0.5,n=20),color="#fc4f30") #绘制该二项式的累积密度函数曲线
#LEGEND 图例
plt.text(x=7.5,y=0.2,s="pmf(binomed)",alpha=0.75,weight="bold",color="#008fd5")
plt.text(x=14.5,y=0.9,s="cdf",rotation=.75,weight="bold",color="#fc4f30")
plt.figure(dpi=100)
#PDF P=0.2
plt.scatter(np.arange(21),stats.binom.pmf(np.arange(21),p=0.2,n=20),alpha=0.75,s=100)
plt.plot(np.arange(21),stats.binom.pmf(np.arange(21),p=0.2,n=20),alpha=0.75)
#PDF P=0.5
plt.scatter(np.arange(21),stats.binom.pmf(np.arange(21),p=0.5,n=20),alpha=0.75,s=100)
plt.plot(np.arange(21),stats.binom.pmf(np.arange(21),p=0.5,n=20),alpha=0.75)
#PDF P=0.9
plt.scatter(np.arange(21),stats.binom.pmf(np.arange(21),p=0.9,n=20),alpha=0.75,s=100)
plt.plot(np.arange(21),stats.binom.pmf(np.arange(21),p=0.9,n=20),alpha=0.75)
#LEGEND 图例
plt.text(x=3.5,y=0.075,s="#p=0.2#",alpha=0.75,weight="bold",color="#008fd5")
plt.text(x=9.5,y=0.075,s="#p=0.5",rotation=.75,weight="bold",color="#fc4f30")
plt.text(x=17.5,y=0.075,s="#p=0.9",rotation=.75,weight="bold",color="#fc4f30")

当P不同时,赢m次的可能性的最大值都出现在均值处,对应概率为n*p。
N对结果的影响:
plt.figure(dpi=100)
#PDF N=10
plt.scatter(np.arange(21),stats.binom.pmf(np.arange(21),p=0.5,n=10),alpha=0.75,s=100)
plt.plot(np.arange(21),stats.binom.pmf(np.arange(21),p=0.5,n=10),alpha=0.75)
#PDF N=15
plt.scatter(np.arange(21),stats.binom.pmf(np.arange(21),p=0.5,n=15),alpha=0.75,s=100)
plt.plot(np.arange(21),stats.binom.pmf(np.arange(21),p=0.5,n=15),alpha=0.75)
#PDF N=20
plt.scatter(np.arange(21),stats.binom.pmf(np.arange(21),p=0.5,n=20),alpha=0.75,s=100)
plt.plot(np.arange(21),stats.binom.pmf(np.arange(21),p=0.5,n=20),alpha=0.75)
#LEGEND 图例
plt.text(x=6,y=0.25,s="$N=0.2$",alpha=0.75,weight="bold",color="#008fd5")
plt.text(x=8,y=0.2,s="$N=0.5$",rotation=.75,weight="bold",color="#fc4f30")
plt.text(x=10,y=0.175,s="$N=0.9$",rotation=.75,weight="bold",color="#fc4f30")
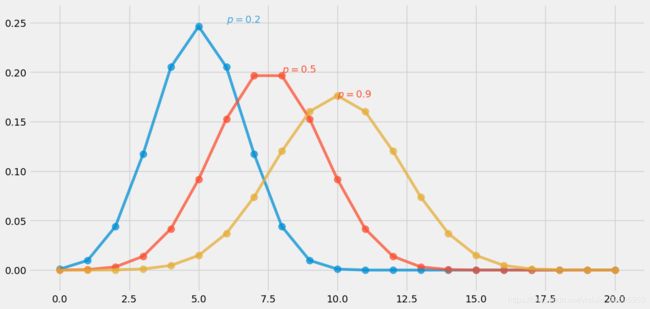
当N不同时,成功m次的可能性的最大值都出现在均值处,对应概率为n*p。
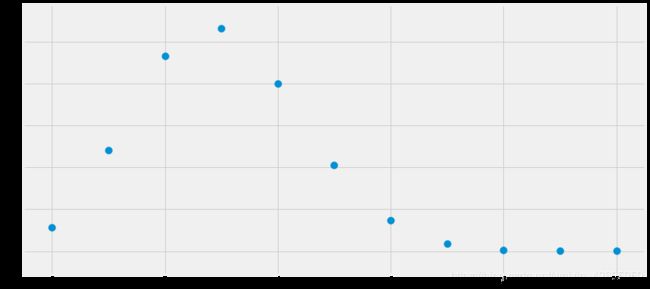
#绘制PMF
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize']=(14,7)
#随机变量x、y的概率
x=1
y=7
print("p(x=1)={}\np(x=7)={}".format(stats.binom.pmf(k=x,p=0.3,n=10),stats.binom.pmf(k=x,p=0.3,n=10)))
#绘制二项式PMF
x_s=np.arange(11)
y_s=stats.binom.pmf(k=x_s,p=0.3,n=10)
plt.scatter(x_s,y_s,s=100) #离散型随机变量用散点图
p(x=1)=0.12106082100000018
p(x=7)=0.12106082100000018
#统计累积概率
#CDF
from scipy.stats import binom
#求成功小于三次的概率
print("p(x<=3) = {}".format(binom.cdf(k=3,p=0.3,n=10)))
#求成功次数大于2次,小于8次的概率
print("p(2< x <=8)={}".format(binom.cdf(k=8,p=0.3,n=10)- binom.cdf(k=2,p=0.3,n=10)))