对鸢尾花数据集和月亮数据集，分别采用LDA、k-means和SVM算法进行二分类可视化分析(python)

对鸢尾花数据集和月亮数据集，分别采用线性LDA、k-means和SVM算法进行二分类可视化分析(python)

一、线性判别分析LDA

1、LDA介绍

线性判别分析(linear discriminant analysis，LDA)是对费舍尔的线性鉴别方法的归纳，这种方法使用统计学，模式识别和机器学习方法，试图找到两类物体或事件的特征的一个线性组合，以能够特征化或区分它们。所得的组合可用来作为一个线性分类器，或者，更常见的是，为后续的分类做降维处理。
线性判别分析是一种经典的线性学习方法，在二分类问题上最早由Fisher在1936年提出，亦称Fisher线性判别。线性判别的思想非常朴素：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近，异样样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的直线上，再根据投影点的位置来确定新样本的类别 。LDA与方差分析（ANOVA）和回归分析紧密相关，这两种分析方法也试图通过一些特征或测量值的线性组合来表示一个因变量。然而，方差分析使用类别自变量和连续数因变量，而判别分析连续自变量和类别因变量（即类标签）。逻辑回归和概率回归比方差分析更类似于LDA，因为他们也是用连续自变量来解释类别因变量的。LDA的基本假设是自变量是正态分布的，当这一假设无法满足时，在实际应用中更倾向于用上述的其他方法。LDA也与主成分分析（PCA）和因子分析紧密相关，它们都在寻找最佳解释数据的变量线性组合。LDA明确的尝试为数据类之间不同建立模型。 另一方面，PCA不考虑类的任何不同，因子分析是根据不同点而不是相同点来建立特征组合。判别的分析不同因子分析还在于，它不是一个相互依存技术：即必须区分出自变量和因变量（也称为准则变量）的不同。在对自变量每一次观察测量值都是连续量的时候，LDA能有效的起作用。当处理类别自变量时，与LDA相对应的技术称为判别反应分析。

优点：
Fisher提出LDA距今已近七十年，仍然是降维和模式分类领域应用中最为广泛采用而且极 为有效的方法之一，其典型应用包括人脸检测、人脸识别、基于视觉飞行的地平线检测、目标跟踪和检测、信用卡欺诈检测和图像检索、语音识别等。之所以有如此广泛的应用，其 主要原因是，LDA（包括其多类推广）具有以下优点：可以直接求得基于广义特征值问题的解析解，从而避免了在一般非线性算法中，如多层感知器，构建中所常遇到的局部最小问题无需对模式的输出类别进行人为的编码，从而使 LDA 对不平衡模式类的处理表现出尤其明显的优势。与神经网络方法相比，LDA 不需要调整参数，因而也不存在学习参数和优化权重以及神经元激活函数的选择等问题；对模式的归一化或随机化不敏感，而这在基于梯度 下降的各种算法中则显得比较突出 [2] 。在某些实际情形中，LDA 具有与基于结构风险最小化原理的支持向量机（SVM）相当的甚至更优的推广性能，但其计算效率则远优于SVM。正则判别分析法（CDA）寻找最优区分类别的坐标轴（k-1个正则坐标，k为类别的数量）。 这些线性函数是不相关的，实际上，它们通过n维数据云定义了一个最优化的k-1个空间，能够最优的区分k个类（通过其在空间的投影）。
多类LDA：当出现超过两类的情况时，可以使用由费舍尔判别派生出的分析方法，它延伸为寻找一个保留了所有类的变化性的子空间。这是由 C.R.Rao 总结出来的。假设，C个类中每一个类都有均值和相同的协方差。
要实现典型的LDA技术前提是所有的样本都必须提前准备完毕。但有些情况下，没有现成的完整数据集或者输入观察数据是流的形式。这样，就要求LDA的特征提取有能力随着观察新样本的增加而更新LDA的特征，而不是在整个数据集上运行算法。例如，在移动机器人或实时脸部识别等实时应用中，提取的LDA特征能随着新观察值实时更新是非常重要的。这种能够通过简单观察新样本来更新LDA特征的技术就叫做增量LDA算法，在过去二十年里，它已经被广泛的研究过。Catterjee和Roychowdhury提出了一种增量自组织LDA算法来更新LDA特征。另外，Demir和Ozmehmet提出利用误差改正和赫布学习规则的线上本地学习算法来更新LDA特征。最后，Aliyari等人提供了快速增量LDA算法。

2、鸢尾花数据集的线性判别分析

#鸢尾花数据集的线性LDA分类
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_classification

class LDA():
    def Train(self, X, y):
       
        X1 = np.array([X[i] for i in range(len(X)) if y[i] == 0])
        X2 = np.array([X[i] for i in range(len(X)) if y[i] == 1])

        # 求中心点
        m1 = np.mean(X1, axis=0)  
        m2 = np.mean(X2, axis=0)
        cov1 = np.dot((X1 - m1).T, (X1 - m1))
        cov2 = np.dot((X2 - m2).T, (X2 - m2))
        Sw = cov1 + cov2
        w = np.dot(np.mat(Sw).I, (m1 - m2).reshape((len(m1), 1)))
        self.m1 = m1  
        self.cov1 = cov1
        self.m2 = m2  
        self.cov2 = cov2
        self.Sw = Sw  # 类内散度矩阵
        self.w = w  # 判别权重矩阵

    def Test(self, X, y):
        y_new = np.dot((X), self.w)
        nums = len(y)
        c1 = np.dot((self.m1 - self.m2).reshape(1, (len(self.m1))), np.mat(self.Sw).I)
        c2 = np.dot(c1, (self.m1 + self.m2).reshape((len(self.m1), 1)))
        c = 1/2 * c2  
        h = y_new - c
        y_hat = []
        for i in range(nums):
            if h[i] >= 0:
                y_hat.append(0)
            else:
                y_hat.append(1)

        count = 0
        for i in range(nums):
            if y_hat[i] == y[i]:
                count += 1
        precise = count / nums
        print("测试样本数量:", nums)
        print("预测正确样本的数量:", count)
        print("测试准确度:", precise)

        return precise

if '__main__' == __name__:
    n_samples = 500
    X, y = make_classification(n_samples=n_samples, n_features=2, n_redundant=0, n_classes=2,
                               n_informative=1, n_clusters_per_class=1, class_sep=0.5, random_state=10)

    lda = LDA()
    Xtrain = X[:299, :]
    Ytrain = y[:299]
    Xtest = X[300:, :]
    Ytest = y[300:]
    lda.Train(Xtrain, Ytrain)
    precise = lda.Test(Xtest, Ytest)

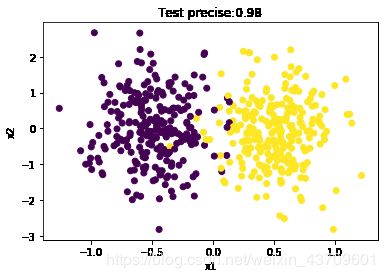
    # 原始数据
    plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
    plt.xlabel("x1")
    plt.ylabel("x2")
    plt.title("Test precise:" + str(precise))
    plt.show()

运行结果：

测试样本数量: 200
预测正确样本的数量: 196
测试准确度: 0.98

3、月亮数据集的线性判别分析

#月亮数据集的线性LDA分析
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
class LDA():
    def Train(self, X, y):
        X1 = np.array([X[i] for i in range(len(X)) if y[i] == 0])
        X2 = np.array([X[i] for i in range(len(X)) if y[i] == 1])
        m1 = np.mean(X1, axis=0)  
        m2 = np.mean(X2, axis=0)
        cov1 = np.dot((X1 - m1).T, (X1 - m1))
        cov2 = np.dot((X2 - m2).T, (X2 - m2))
        Sw = cov1 + cov2
        w = np.dot(np.mat(Sw).I, (m1 - m2).reshape((len(m1), 1)))
        self.m1 = m1  
        self.cov1 = cov1
        self.m2 = m2  
        self.cov2 = cov2
        self.Sw = Sw  
        self.w = w  
    def Test(self, X, y):
        y_new = np.dot((X), self.w)
        # 计算fisher线性判别式
        nums = len(y)
        c1 = np.dot((self.m1 - self.m2).reshape(1, (len(self.m1))), np.mat(self.Sw).I)
        c2 = np.dot(c1, (self.m1 + self.m2).reshape((len(self.m1), 1)))
        c = 1/2 * c2  # 2个分类的中心
        h = y_new - c
        # 判别
        y_hat = []
        for i in range(nums):
            if h[i] >= 0:
                y_hat.append(0)
            else:
                y_hat.append(1)
        # 计算分类精度
        count = 0
        for i in range(nums):
            if y_hat[i] == y[i]:
                count += 1
        precise = count / (nums+0.000001)
        # 显示信息
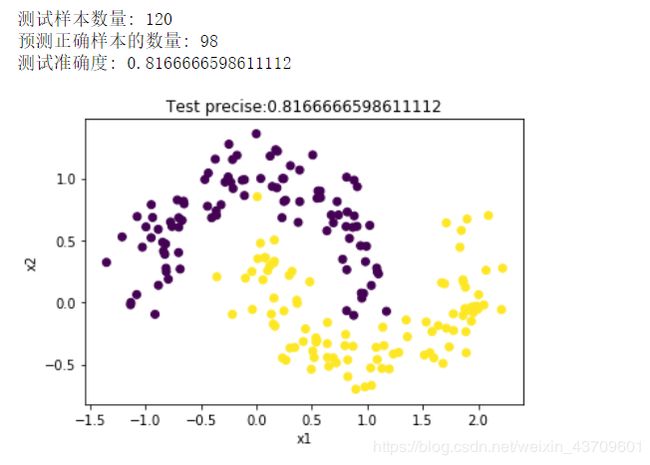
        print("测试样本数量:", nums)
        print("预测正确样本的数量:", count)
        print("测试准确度:", precise)
        return precise
if '__main__' == __name__:
    X, y = make_moons(n_samples=200, noise=0.15, random_state=42)
    lda = LDA()
    Xtrain = X[:120, :]
    Ytrain = y[:120]
    Xtest = X[80:, :]
    Ytest = y[80:]
    lda.Train(Xtrain, Ytrain)
    precise = lda.Test(Xtest, Ytest)
    plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
    plt.xlabel("x1")
    plt.ylabel("x2")
    plt.title("Test precise:" + str(precise))
    plt.show()

运行结果：

二、K-means

1、K-means介绍

k均值聚类算法（k-means clustering algorithm）是一种迭代求解的聚类分析算法，其步骤是，预将数据分为K组，则随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。

聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程，聚类就是一种发现这种内在结构的技术，聚类技术经常被称为无监督学习。
k均值聚类是最著名的划分聚类算法，由于简洁和效率使得他成为所有聚类算法中最广泛使用的。给定一个数据点集合和需要的聚类数目k，k由用户指定，k均值算法根据某个距离函数反复把数据分入k个聚类中。

算法：
先随机选取K个对象作为初始的聚类中心。然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。一旦全部对象都被分配了，每个聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是以下任何一个：
1)没有（或最小数目）对象被重新分配给不同的聚类。
2)没有（或最小数目）聚类中心再发生变化。
3)误差平方和局部最小。

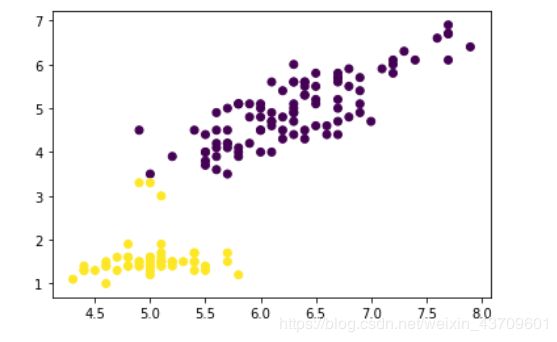
2、鸢尾花数据集的K-means聚类分析

#鸢尾花数据集的K-means分类
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
 
#加载数据集，是一个字典类似Java中的map
lris_df = datasets.load_iris()
 
#挑选出前两个维度作为x轴和y轴，你也可以选择其他维度
x_axis = lris_df.data[:,0]
y_axis = lris_df.data[:,2]
 
 
#这里已经知道了分2类，其他分类这里的参数需要调试
model = KMeans(n_clusters=2)
 
#训练模型
model.fit(lris_df.data)
 
#选取行标为100的那条数据，进行预测
prddicted_label= model.predict([[6.3, 3.3, 6, 2.5]])
 
#预测全部150条数据
all_predictions = model.predict(lris_df.data)
 
#打印出来对150条数据的聚类散点图
plt.scatter(x_axis, y_axis, c=all_predictions)
plt.show()

运行结果：

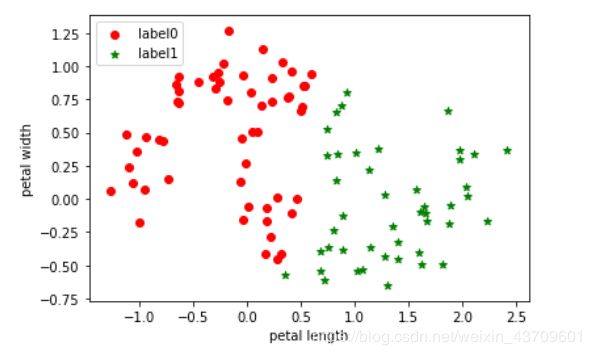
3、月亮数据集的K-means聚类分析

#月亮数据集的K-means分类
#月亮数据集的K-means分类
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
model = KMeans(n_clusters=2)#构造聚类器
model.fit(X)#聚类
label_pred = model.labels_ #获取聚类标签
#绘制k-means结果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
plt.scatter(x0[:, 0], x0[:, 1], c = "red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c = "green", marker='*', label='label1')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()

运行结果：

三、SVM算法

1、介绍

支持向量机（Support Vector Machine, SVM）是一类按监督学习（supervised learning）方式对数据进行二元分类的广义线性分类器（generalized linear classifier），其决策边界是对学习样本求解的最大边距超平面（maximum-margin hyperplane） 。
SVM使用铰链损失函数（hinge loss）计算经验风险（empirical risk）并在求解系统中加入了正则化项以优化结构风险（structural risk），是一个具有稀疏性和稳健性的分类器 。SVM可以通过核方法（kernel method）进行非线性分类，是常见的核学习（kernel learning）方法之一 。
SVM被提出于1964年，在二十世纪90年代后得到快速发展并衍生出一系列改进和扩展算法，在人像识别、文本分类等模式识别（pattern recognition）问题中有得到应用 。

SVM是由模式识别中广义肖像算法（generalized portrait algorithm）发展而来的分类器 ，其早期工作来自前苏联学者Vladimir N. Vapnik和Alexander Y. Lerner在1963年发表的研究 。1964年，Vapnik和Alexey Y. Chervonenkis对广义肖像算法进行了进一步讨论并建立了硬边距的线性SVM 。此后在二十世纪70-80年代，随着模式识别中最大边距决策边界的理论研究 、基于松弛变量（slack variable）的规划问题求解技术的出现 ，和VC维（Vapnik-Chervonenkis dimension, VC dimension）的提出 ，SVM被逐步理论化并成为统计学习理论的一部分 。1992年，Bernhard E. Boser、Isabelle M. Guyon和Vapnik通过核方法得到了非线性SVM 。1995年，Corinna Cortes和Vapnik提出了软边距的非线性SVM并将其应用于手写字符识别问题 ，这份研究在发表后得到了关注和引用，为SVM在各领域的应用提供了参考。

2、鸢尾花数据集的SVM分析

#鸢尾花数据集的SVM分析
# 使用sklearn的函数来获取MNIST数据集
from sklearn.datasets import fetch_openml
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# 为了显示中文
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

from sklearn.svm import SVC
from sklearn import datasets

iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # petal length, petal width
y = iris["target"]

setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]

# SVM Classifier model
svm_clf = SVC(kernel="linear", C=float("inf"))
svm_clf.fit(X, y)

def plot_svc_decision_boundary(svm_clf, xmin, xmax):
    # 获取决策边界的w和b
    w = svm_clf.coef_[0]
    b = svm_clf.intercept_[0]

    # At the decision boundary, w0*x0 + w1*x1 + b = 0
    # => x1 = -w0/w1 * x0 - b/w1
    x0 = np.linspace(xmin, xmax, 200)
    # 画中间的粗线
    decision_boundary = -w[0]/w[1] * x0 - b/w[1]
    # 计算间隔
    margin = 1/w[1]
    gutter_up = decision_boundary + margin
    gutter_down = decision_boundary - margin
    # 获取支持向量
    svs = svm_clf.support_vectors_
    plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
    plt.plot(x0, decision_boundary, "k-", linewidth=2)
    plt.plot(x0, gutter_up, "k--", linewidth=2)
    plt.plot(x0, gutter_down, "k--", linewidth=2)
# Bad models
x0 = np.linspace(0, 5.5, 200)
# 随便画的
pred_1 = 5*x0 - 20
pred_2 = x0 - 1.8
pred_3 = 0.1 * x0 + 0.5

plt.figure(figsize=(12,2.7))

plt.subplot(121)
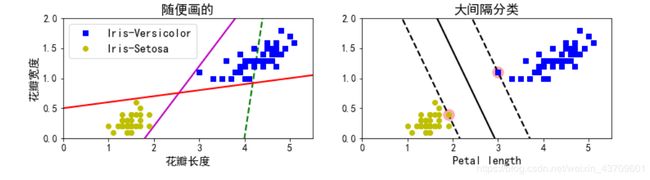
plt.title("随便画的", fontsize=16)
plt.plot(x0, pred_1, "g--", linewidth=2)
plt.plot(x0, pred_2, "m-", linewidth=2)
plt.plot(x0, pred_3, "r-", linewidth=2)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
plt.xlabel("花瓣长度", fontsize=14)
plt.ylabel("花瓣宽度", fontsize=14)

plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 5.5, 0, 2])

plt.subplot(122)
plt.title("大间隔分类", fontsize=16)
plot_svc_decision_boundary(svm_clf, 0, 5.5)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo")
plt.xlabel("Petal length", fontsize=14)
plt.axis([0, 5.5, 0, 2])
plt.show()

运行结果：

3、月亮数据集的SVM分析

#月亮数据集的SVM分析
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
import numpy as np
import matplotlib as mpl
from sklearn.datasets import make_moons
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
# 为了显示中文
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
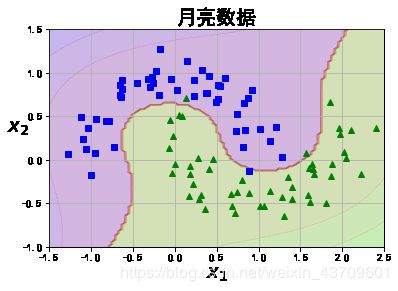
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
def plot_dataset(X, y, axes):
    plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
    plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
    plt.axis(axes)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=20)
    plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
    plt.title("月亮数据",fontsize=20)
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()

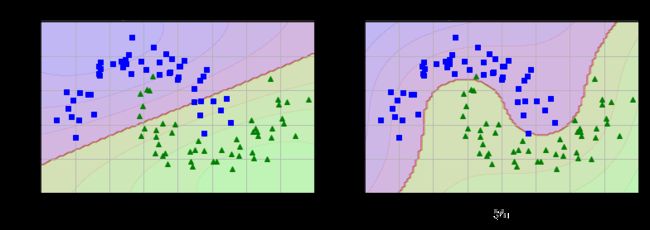
polynomial_svm_clf = Pipeline([
        # 将源数据 映射到 3阶多项式
        ("poly_features", PolynomialFeatures(degree=3)),
        # 标准化
        ("scaler", StandardScaler()),
        # SVC线性分类器
        ("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42))
    ])
polynomial_svm_clf.fit(X, y)
def plot_predictions(clf, axes):
    # 打表
    x0s = np.linspace(axes[0], axes[1], 100)
    x1s = np.linspace(axes[2], axes[3], 100)
    x0, x1 = np.meshgrid(x0s, x1s)
    X = np.c_[x0.ravel(), x1.ravel()]
    y_pred = clf.predict(X).reshape(x0.shape)
    y_decision = clf.decision_function(X).reshape(x0.shape)
#     print(y_pred)
#     print(y_decision)  
    plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
    plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)
plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()

from sklearn.svm import SVC
gamma1, gamma2 = 0.1, 5
C1, C2 = 0.001, 1000
hyperparams = (gamma1, C1), (gamma1, C2)
svm_clfs = []
for gamma, C in hyperparams:
    rbf_kernel_svm_clf = Pipeline([
            ("scaler", StandardScaler()),
            ("svm_clf", SVC(kernel="rbf", gamma=gamma, C=C))
        ])
    rbf_kernel_svm_clf.fit(X, y)
    svm_clfs.append(rbf_kernel_svm_clf)
plt.figure(figsize=(11, 7))
for i, svm_clf in enumerate(svm_clfs):
    plt.subplot(221 + i)
    plot_predictions(svm_clf, [-1.5, 2.5, -1, 1.5])
    plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
    gamma, C = hyperparams[i]
    plt.title(r"$\gamma = {}, C = {}$".format(gamma, C), fontsize=16)
plt.tight_layout()
plt.show()

四、SVM算法的优缺点

1、优点

SVM理论提供了一种避开高维空间的复杂性,直接用此空间的内积函数(既是核函数),再利用在线性可分的情况下的求解方法直接求解对应的高维空间的决策问题.当核函数已知,可以简化高维空间问题的求解难度.同时SVM是基于小样本统计理论的基础上的,这符合机器学习的目的.而且支持向量机比神经网络具有较好的泛化推广能力.

2、缺点

对于每个高维空间在此空间的映射F,如何确定F也就是核函数,现在还没有合适的方法,所以对于一般的问题,SVM只是把高维空间的复杂性的困难转为了求核函数的困难.而且即使确定核函数以后,在求解问题分类时,要求解函数的二次规划,这就需要大量的存储空间.这也是SVM的一个问题。