jupyter编程完成对手写体Mnist数据集中10个字符 (0-9)的分类识别
MNIST
数据介绍:使用MNIST数据集,这是一组由美国高中生和人口调查局员工手写的70000个数字的图片。每张图像都用其代表的数字标记。这个数据集被广为使用,因此也被称作是机器学习领域的“Hello World”:但凡有人想到了一个新的分类算法,都会想看看在MNIST上的执行结果。因此只要是学习机器学习的人,早晚都要面对MNIST。
# 使用sklearn的函数来获取MNIST数据集
from sklearn.datasets import fetch_openml
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# 为了显示中文
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
# 耗时巨大
def sort_by_target(mnist):
reorder_train=np.array(sorted([(target,i) for i, target in enumerate(mnist.target[:60000])]))[:,1]
reorder_test=np.array(sorted([(target,i) for i, target in enumerate(mnist.target[60000:])]))[:,1]
mnist.data[:60000]=mnist.data[reorder_train]
mnist.target[:60000]=mnist.target[reorder_train]
mnist.data[60000:]=mnist.data[reorder_test+60000]
mnist.target[60000:]=mnist.target[reorder_test+60000]
import time
start_time=time.clock()
mnist=fetch_openml('mnist_784',version=1,cache=True)
mnist.target=mnist.target.astype(np.int8)
sort_by_target(mnist)
stop_time=time.clock()
cost=stop_time-start_time
print(cost)
#这个地方运行的时间比较久,可以写个计时器来查看运行时间
C:\Users\LOL\Anaconda3\envs\tensorflow\lib\site-packages\ipykernel_launcher.py:2: DeprecationWarning: time.clock has been deprecated in Python 3.3 and will be removed from Python 3.8: use time.perf_counter or time.process_time instead
29.66786209999964
C:\Users\LOL\Anaconda3\envs\tensorflow\lib\site-packages\ipykernel_launcher.py:6: DeprecationWarning: time.clock has been deprecated in Python 3.3 and will be removed from Python 3.8: use time.perf_counter or time.process_time instead
由于电脑性能的不同,每个人运行的时间不同,一般为20几秒或者30几秒
mnist["data"], mnist["target"]
(array([[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]),
array([0, 0, 0, ..., 9, 9, 9], dtype=int8))
显示维度:
mnist.data.shape
(70000, 784)
X,y=mnist["data"],mnist["target"]
X.shape
(70000, 784)
y.shape
(70000,)
28*28
784
# 展示图片
def plot_digit(data):
image = data.reshape(28, 28)
plt.imshow(image, cmap = mpl.cm.binary,
interpolation="nearest")
plt.axis("off")
some_digit = X[36000]
plot_digit(X[36000].reshape(28,28))
y[36000]
5
# 更好看的图片展示
def plot_digits(instances,images_per_row=10,**options):
size=28
# 每一行有一个
image_pre_row=min(len(instances),images_per_row)
images=[instances.reshape(size,size) for instances in instances]
# 有几行
n_rows=(len(instances)-1) // image_pre_row+1
row_images=[]
n_empty=n_rows*image_pre_row-len(instances)
images.append(np.zeros((size,size*n_empty)))
for row in range(n_rows):
# 每一次添加一行
rimages=images[row*image_pre_row:(row+1)*image_pre_row]
# 对添加的每一行的额图片左右连接
row_images.append(np.concatenate(rimages,axis=1))
# 对添加的每一列图片 上下连接
image=np.concatenate(row_images,axis=0)
plt.imshow(image,cmap=mpl.cm.binary,**options)
plt.axis("off")
plt.figure(figsize=(9,9))
example_images=np.r_[X[:12000:600],X[13000:30600:600],X[30600:60000:590]]
plot_digits(example_images,images_per_row=10)
plt.show()
接下来,我们需要创建一个测试集,并把其放在一边。
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
同样,我们还需要对训练集进行洗牌,这样可以保证交叉验证的时候,所有的折叠都差不多。此外,有些机器学习算法对训练示例的循序敏感,如果连续输入许多相似的实例,可能导致执行的性能不佳。给数据洗牌,正是为了确保这种情况不会发生。
import numpy as np
shuffer_index=np.random.permutation(60000)
X_train,y_train=X_train[shuffer_index],y_train[shuffer_index]
训练一个二分类器
现在,我们先简化问题,只尝试识别一个数字,比如数字5,那么这个"数字5检测器",就是一个二分类器的例子,它只能区分两个类别:5和非5。先为此分类任务创建目录标量
y_train_5=(y_train==5)
y_test_5=(y_test==5)
接着挑选一个分类器并开始训练。一个好的选择是随机梯度下降(SGD)分类器,使用sklearn的SGDClassifier类即可。这个分类器的优势是:能够有效处理非常大型的数据集。这部分是因为SGD独立处理训练实例,一次一个(这也使得SGD非常适合在线学习任务)。
from sklearn.linear_model import SGDClassifier
sgd_clf=SGDClassifier(max_iter=5,tol=-np.infty,random_state=42)
sgd_clf.fit(X_train,y_train_5)
SGDClassifier(alpha=0.0001, average=False, class_weight=None,
early_stopping=False, epsilon=0.1, eta0=0.0, fit_intercept=True,
l1_ratio=0.15, learning_rate='optimal', loss='hinge', max_iter=5,
n_iter_no_change=5, n_jobs=None, penalty='l2', power_t=0.5,
random_state=42, shuffle=True, tol=-inf, validation_fraction=0.1,
verbose=0, warm_start=False)
sgd_clf.predict([some_digit])
array([ True])
性能考核
评估分类器比评估回归器要困难很多,因此本章将会用很多篇幅来讨论这个主题,同时也会涉及许多性能考核的方法。
使用交叉验证测量精度
随机交叉验证和分层交叉验证效果对比
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")
array([0.96225, 0.9645 , 0.94765])
# 类似于分层采样,每一折的分布类似
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone
skfolds = StratifiedKFold(n_splits=3, random_state=42)
for train_index, test_index in skfolds.split(X_train, y_train_5):
clone_clf = clone(sgd_clf)
X_train_folds = X_train[train_index]
y_train_folds = (y_train_5[train_index])
X_test_fold = X_train[test_index]
y_test_fold = (y_train_5[test_index])
clone_clf.fit(X_train_folds, y_train_folds)
y_pred = clone_clf.predict(X_test_fold)
n_correct = sum(y_pred == y_test_fold)
print(n_correct / len(y_pred))
C:\Users\LOL\Anaconda3\envs\tensorflow\lib\site-packages\sklearn\model_selection\_split.py:296: FutureWarning: Setting a random_state has no effect since shuffle is False. This will raise an error in 0.24. You should leave random_state to its default (None), or set shuffle=True.
FutureWarning
0.96225
0.9645
0.94765
我们可以看到两种交叉验证的准确率都达到了95%上下,看起来很神奇,不过在开始激动之前,让我们来看一个蠢笨的分类器,将所有图片都预测为‘非5’
from sklearn.base import BaseEstimator
# 随机预测模型
class Never5Classifier(BaseEstimator):
def fit(self, X, y=None):
pass
def predict(self, X):
return np.zeros((len(X), 1), dtype=bool)
never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy")
array([0.909 , 0.90715, 0.9128 ])
我们可以看到,准确率也超过了90%!这是因为我们只有大约10%的图像是数字5,所以只要猜一张图片不是5,那么有90%的时间都是正确的,简直超过了大预言家。
这说明,准确率通常无法成为分类器的首要性能指标,特别是当我们处理偏斜数据集的时候(也就是某些类别比其他类更加频繁的时候)
混淆矩阵
评估分类器性能的更好的方法是混淆矩阵。总体思路就是统计A类别实例被分成B类别的次数。例如,要想知道分类器将数字3和数字5混淆多少次,只需要通过混淆矩阵的第5行第3列来查看。
要计算混淆矩阵,需要一组预测才能将其与实际目标进行比较。当然可以通过测试集来进行预测,但是现在我们不动它(测试集最好保留到项目的最后,准备启动分类器时再使用)。最为代替,可以使用cross_val_predict()函数:
cross_val_predict 和 cross_val_score 不同的是,前者返回预测值,并且是每一次训练的时候,用模型没有见过的数据来预测
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)
array([[53417, 1162],
[ 1350, 4071]], dtype=int64)
上面的结果表明:第一行所有’非5’(负类)的图片中,有53417被正确分类(真负类),1162,错误分类成了5(假负类);第二行表示所有’5’(正类)的图片中,有1350错误分类成了非5(假正类),有4071被正确分类成5(真正类).
一个完美的分类器只有真正类和真负类,所以其混淆矩阵只会在其对角线(左上到右下)上有非零值
y_train_perfect_predictions = y_train_5
confusion_matrix(y_train_5, y_train_perfect_predictions)
array([[54579, 0],
[ 0, 5421]], dtype=int64)
混淆矩阵能提供大量信息,但有时我们可能会希望指标简洁一些。正类预测的准确率是一个有意思的指标,它也称为分类器的精度(如下)。
P r e c i s i o n ( 精 度 ) = T P T P + F P Precision(精度)=\frac{TP}{TP+FP} Precision(精度)=TP+FPTP
其中TP是真正类的数量,FP是假正类的数量。
做一个简单的正类预测,并保证它是正确的,就可以得到完美的精度(精度=1/1=100%)
这并没有什么意义,因为分类器会忽略这个正实例之外的所有内容。因此,精度通常会与另一个指标一起使用,这就是召回率,又称为灵敏度或者真正类率(TPR):它是分类器正确检测到正类实例的比率(如下):
R e c a l l ( 召 回 率 ) = T P T P + F N Recall(召回率)=\frac{TP}{TP+FN} Recall(召回率)=TP+FNTP
FN是假负类的数量
精度和召回率
# 使用sklearn的工具度量精度和召回率
from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred)
0.7779476399770686
recall_score(y_train_5, y_train_pred)
0.7509684560044272
我们可以看到,这个5-检测器,并不是那么好用,大多时候,它说一张图片为5时,只有77%的概率是准确的,并且也只有75%的5被检测出来了
下面,我们可以将精度和召回率组合成单一的指标,称为F1分数。
F 1 = 2 1 P r e c i s i o n + 1 R e c a l l = 2 ∗ P r e ∗ R e c P r e + R e c = T P T P + F N + F P 2 F_1=\frac{2}{\frac{1}{Precision}+\frac{1}{Recall}}=2*\frac{Pre*Rec}{Pre+Rec}=\frac{TP}{TP+\frac{FN+FP}{2}} F1=Precision1+Recall12=2∗Pre+RecPre∗Rec=TP+2FN+FPTP
要计算F1分数,只需要调用f1_score()即可
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)
0.7642200112633752
F1分数对那些具有相近的精度和召回率的分类器更为有利。这不一定一直符合预期,因为在某些情况下,我们更关心精度,而另一些情况下,我们可能真正关系的是召回率。
例如:假设训练一个分类器来检测儿童可以放心观看的视频,那么我们可能更青睐那种拦截了好多好视频(低召回率),但是保留下来的视频都是安全(高精度)的分类器,而不是召回率虽高,但是在产品中可能会出现一些非常糟糕的视频分类器(这种情况下,你甚至可能会添加一个人工流水线来检查分类器选出来的视频)。
反过来说,如果你训练一个分类器通过图像监控来检测小偷:你大概可以接受精度只有30%,只要召回率能达到99%。(当然,安保人员会接收到一些错误的警报,但是几乎所有的窃贼都在劫难逃)
遗憾的是,鱼和熊掌不可兼得:我们不能同时增加精度并减少召回率,反之亦然,这称为精度/召回率权衡
精度/召回率权衡
在分类中,对于每个实例,都会计算出一个分值,同时也有一个阈值,大于为正例,小于为负例。通过调节这个阈值,可以调整精度和召回率。
y_scores = sgd_clf.decision_function([some_digit])
y_scores
array([150526.40944343])
threshold = 0
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred
array([ True])
threshold = 200000
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred
array([False])
# 返回决策分数,而不是预测结果
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,
method="decision_function")
y_scores.shape
(60000,)
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
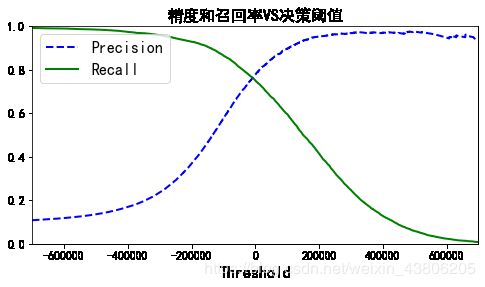
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
plt.xlabel("Threshold", fontsize=16)
plt.title("精度和召回率VS决策阈值", fontsize=16)
plt.legend(loc="upper left", fontsize=16)
plt.ylim([0, 1])
plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.xlim([-700000, 700000])
plt.show()
可以看见,随着阈值提高,召回率下降了,也就是说,有真例被判负了,精度上升,也就是说,有部分原本被误判的负例,被丢出去了。
你可以会好奇,为什么精度曲线会比召回率曲线要崎岖一些,原因在于,随着阈值提高,精度也有可能会下降 4/5 => 3/4(虽然总体上升)。另一方面,阈值上升,召回率只会下降。
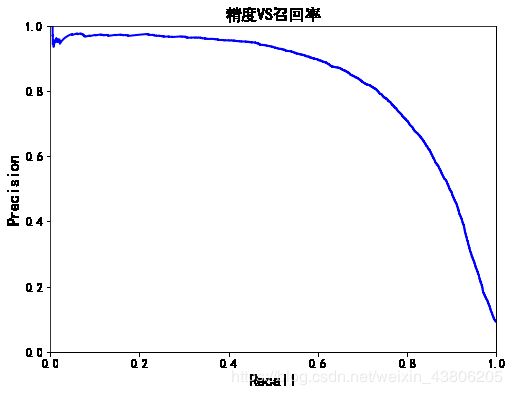
现在就可以轻松通过选择阈值来实现最佳的精度/召回率权衡了。还有一种找到最好的精度/召回率权衡的方法是直接绘制精度和召回率的函数图。
def plot_precision_vs_recall(precisions, recalls):
plt.plot(recalls, precisions, "b-", linewidth=2)
plt.xlabel("Recall", fontsize=16)
plt.title("精度VS召回率", fontsize=16)
plt.ylabel("Precision", fontsize=16)
plt.axis([0, 1, 0, 1])
plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
plt.show()
可以看见,从80%的召回率往右,精度开始急剧下降。我们可能会尽量在这个陡降之前选择一个精度/召回率权衡–比如召回率60%以上。当然,如何选择取决于你的项目。
假设我们决定瞄准90%的精度目标。通过绘制的第一张图(放大一点),得出需要使用的阈值大概是70000.要进行预测(现在是在训练集上),除了调用分类器的predict方法,也可以使用这段代码:
y_train_pred_90 = (y_scores > 70000)
precision_score(y_train_5, y_train_pred_90)
0.8712083540527101
recall_score(y_train_5, y_train_pred_90)
0.6463752075262866
现在我们就有了一个精度接近90%的分类器了,如果有人说,“我们需要99%的精度。”,那么我就要问:“召回率是多少?”
ROC曲线
还有一种经常与二元分类器一起使用的工具,叫做受试者工作特征曲线(简称ROC)。它与精度/召回率曲线非常相似,但绘制的不是精度和召回率,而是真正类率(召回率的另一种称呼)和假正类率(FPR)。FPR是被错误分为正类的负类实例比率。它等于1-真负类率(TNR),后者正是被正确分类为负类的负类实例比率,也称为奇异度。因此ROC曲线绘制的是灵敏度和(1-奇异度)的关系
| ~ | 1 | 0 |
|---|---|---|
| 1 | TP | FN |
| 0 | FP | TN |
F P R = F P F P + T N FPR=\frac{FP}{FP+TN} FPR=FP+TNFP
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
# 使用 roc_curve()函数计算多种阈值的TPR和FPR
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
def plot_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1], [0, 1], 'k--')
plt.axis([0, 1, 0, 1])
plt.xlabel('False Positive Rate', fontsize=16)
plt.ylabel('True Positive Rate', fontsize=16)
plt.figure(figsize=(8, 6))
plot_roc_curve(fpr, tpr)
plt.show()
这里同样面对一个折中权衡:召回率(TPR)很高,分类器产生的假正类(FPR)就越多。虚线表示纯随机的ROC曲线;一个优秀的分类器(向左上角)。
有一种比较分类器的方式是测量曲线下面积(AUC)。完美的ROC AUC等于1,纯随机分类的ROC AUC等于0.5
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)
0.9562435587387078
ROC曲线和精度/召回率(或PR)曲线非常相似,因此,你可能会问,如何决定使用哪种曲线。
一个经验法则是,当正类非常少见或者你更关注假正类而不是假负类时,应该选择PR曲线,反之选择ROC曲线。
例如,看前面的ROC曲线图时,以及ROC AUC分数时,你可能会觉得分类器真不错。但这主要是应为跟负类(非5)相比,正类(数字5)的数量真的很少。相比之下,PR曲线清楚地说明分类器还有改进的空间(曲线还可以更接近右上角)
训练一个随机森林分类器,并计算ROC和ROC AUC分数
# 具体RF的原理,第七章介绍
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(n_estimators=10, random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
method="predict_proba")
y_scores_forest = y_probas_forest[:, 1] # score = proba of positive class
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5,y_scores_forest)
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, "b:", linewidth=2, label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.title("SGD和RL的ROC曲线对比")
plt.legend(loc="lower right", fontsize=16)
plt.show()
roc_auc_score(y_train_5, y_scores_forest)
0.9931243366003829