蒙提霍尔问题的概率原理及随机化模拟(也称三门问题,Java语言描述)
问题引入
人们常说:“相信自己的直觉”、“跟着自己的直觉走,没错的”、“要坚定自己的路”……
不是说这些话不对,但有时候结果还真不是我们直觉能get到的……
这是一个有趣的问题——三门问题,希望给大家一些启发。
三门问题
三门问题(Monty Hall problem)亦称为蒙提霍尔问题、蒙特霍问题或蒙提霍尔悖论,大致出自美国的电视游戏节目Let’s Make a Deal。问题名字来自该节目的主持人蒙提·霍尔(Monty Hall)。参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车,选中后面有车的那扇门可赢得该汽车,另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,节目主持人开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是:换另一扇门会否增加参赛者赢得汽车的机率?如果严格按照上述的条件,即主持人清楚地知道,自己打开的那扇门后是羊,那么答案是会。不换门的话,赢得汽车的几率是1/3。换门的话,赢得汽车的几率是2/3。
这个问题亦被叫做蒙提霍尔悖论:虽然该问题的答案在逻辑上并不自相矛盾,但十分违反直觉。这问题曾引起一阵热烈的讨论。
Java模拟验证
这次也不能说是什么编程实现了,只能说做个随机化模拟吧,把数据量开的大一些,就1’000’000吧,问题不大。
这个模拟的思路就是我们用一个set,装 0, 1, 2 三个数字,模拟三扇门,然后先随机生成一下0~2之间的一个随机数(也就是真正的汽车所在位置)。
接下来我们随机生成一个参赛者的选择(他没有任何场外信息,只能三蒙一),由于我们模拟的是选手更改选择的情况,所以这个就没什么意义了,那就删去它。
然后还要随机生成一个主持人打开的门。主持人显然是知道车在哪里的,不论被没被参赛者第一次选中,主持人都只会打开一扇空门(也就是藏有山羊的门)。这个随机序号不能与真正的结果重合,也不能与选手选中的序号重合(这两种情况也可能重合)。这个序列也删去它。
一共只有三个数,删了两个,就只剩一个了。我们做的模拟是选手选择换门,所以剩下的门就是他选的答案,看一看与最初的随机答案一不一致就行。
最后概率竟是2/3。
import java.util.HashSet;
import java.util.Random;
import java.util.Set;
public class Main {
public static void main(String[] args) {
int times = 1000000;
int winNum = 0;
Set<Integer> set = new HashSet<>();
Random random = new Random();
for (int i = 0; i < times; i++) {
set.add(0);
set.add(1);
set.add(2);
//车在随机一个门后面
int result = random.nextInt(3);
//从三个门里面盲猜一个门
int guessNum = random.nextInt(3);
//剔除选项
set.remove(guessNum);
int removeNum = 3;
while (removeNum == result || removeNum == guessNum) {
removeNum = random.nextInt(3);
}
//主持人再删一个
set.remove(removeNum);
if (set.contains(result)) {
winNum++;
}
}
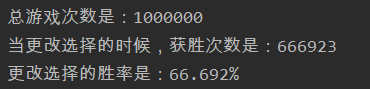
System.out.println("总游戏次数是:" + times);
System.out.println("当更改选择的时候,获胜次数是:" + winNum);
System.out.printf("更改选择的胜率是:%.3f%%", (double)winNum/times*100);
}
}
原理
不能只是知其然,更要知其所以然。
这个问题的分析还要回归到概率论上。
容易理解的分析
先给一个不规范的分析,更好理解:
试想原先三蒙一,概率确实是1/3,但反过来考虑,不是第一次选中的概率是2/3,那在主持人帮我们排掉一个不可能情况的情况下,我们换成没人动过的门,成功的概率是2/3,是大于我们“坚持信仰”概率的。
穷举分析
再给一个穷举的分析,本问题情况少,容易穷举:
A,B,C 三个值,按照换门的策略模拟:
| 初选 | 主持人选 | 剩下的 | 正确答案 | 是否猜对 |
|---|---|---|---|---|
| A | B | C | A | N |
| A | C | B | A | N |
| B | C | A | A | Y |
| C | B | A | A | Y |
| A | C | B | B | Y |
| B | A | C | B | Y |
| B | C | A | B | Y |
| C | A | B | B | Y |
| A | B | C | C | Y |
| B | A | C | C | Y |
| C | A | B | C | N |
| C | B | A | C | N |
统计基本事件,古典概型算概率得到P=2/3。
详细分析
主持人其实没啥用,所以可以不看:
第一次选的空门(概率66.6%),之后主持人开另一个空门,换门,得到汽车。
第一次选的汽车(概率33.3%),之后主持人开另一个空门,不换门,得到汽车。
这里影响到结果的概率问题只发生在第一次选门上,如果条件如上设置,当一开始的门选定后,事件的结果也就决定了,所以这里不存在之后主持人是选择1号空门,还是2号空门的问题,所以在做概率计算是不考虑主持人的选择。
如果也要考虑主持人的话:
第一次选的空门1(概率1/3),之后主持人开另一个空门,换门,得到汽车。事件总概率1/3。
第一次选的空门2(概率1/3),之后主持人开另一个空门,换门,得到汽车。事件总概率1/3。
第一次选的汽车(概率1/3),之后主持人开另一个空门1(概率1/2),不换门,得到汽车 这个事件总概率
。
第一次选的汽车(概率1/3),之后主持人开另一个空门2(概率1/2),不换门,得到汽车 这个事件总概率
。
主持人选1号空门还是2号空门打开,这里有个主持人的选择概率,我假设的是主持人随机选择(抽签或者随意),所以各给了50%的概率,如果主持人就是喜欢1号空门,必开1号,那么也就成了1号(100%),2号(0%)了,最后结果并不影响。
所以开始选中汽车,最后换门不得奖的概率是33.3%,开始选中空门,换门最后得奖的概率是66.6%。
当然了,其实分析题意就知道主持人这边与概率根本没有关系,所以真的不必考虑他。
Ending……
类似问题(Update on 2020.2.23)
找到了一篇博客,也是类似的问题。
仔细看看就能加深理解啦!