【你也能看得懂的电磁场与电磁波系列连载 17】

在上一个连载里面，我们废了好大的力气介绍了全微分，我们回顾一下：

---

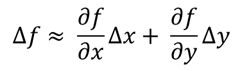
下面，我们再看一个事情：对于二元函数（曲面）上的某一点，以它为起点是可以引出无数条射线的对吧，而这些射线的方向也是无穷多个的，朝着四面八方（不过都是平行于 xoy面的）。而这些射线也会对应着曲面上的一段曲线。

这里解释一下为什么是平行于 xoy 面：而根据线性代数里面的知识，我们知道空间中的任何一个向量都可以用标准正交基来表示。在二元函数里面我们可以用 $\overline{a_x},\overline{a_y}$ 的线性组合来表示向量，那你不管 $\overline{a_x},\overline{a_y}$ 怎么组合，所构成的向量不都是于 xoy 平行的嘛。

那么以 $M_0$ 为起点的这一条射线（方向向量）所对应的二元函数上的一段曲线也是有导数的，这个导数我们就叫做方向导数（顾名思义，就是沿着这个方向上曲线的导数）如下图：

那么，很自然地我们就可以理解：如果经过 M0 的射线方向刚好是平行于 $y$ 轴的，那么所截得的曲线的导数就是对 $y$ 的偏导数了；如果经过 M0 的射线方向刚好是平行于 $x$ 轴的，那么所截得的曲线的导数就是对 $x$ 的偏导数了。（所以说：偏导数就是 $f(x,y)$ 沿着对应坐标轴所截得得曲线得导数）

我们看一下以 $M_0$ 为起点，$\overline{△l}$为方向所对应到 $f(x,y)$的一条曲线 $M_{0}M$

曲线 $M_{0}M$的导数就是方向导数，根据导数的定义我们可以有：

我们看到：$f(M)-f(M_0)$ 就是 $△f$！是不是有点熟悉的感觉了？对！我们利用上一个连载所推导的公式：

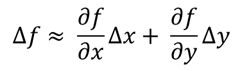
而根据线性代数里面的知识，我们知道空间中的任何一个向量都可以用标准正交基来表示。$\overline{△l}$ 不就是平面中的一个向量吗！如下图所示：

也就是说：

我们再回过头看这个式子：

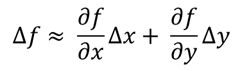
根据向量点乘的性质，我们是不是可以这样分解一下：

---

接下来对于：

我们还想把它改写成与 $△l$ 有关的表达式，那么我们就会引入方向余弦的概念了。

上面这个图直观地描述了方向余弦的求法，那么，对于上面的式子，我们就可以改写成：

---

因此，$△f$就可以写成：

细心的大家应该看到了这样的表达式：

我们就把他定义为：

这就是函数 $f(x,y)$ 的梯度。

---

我们再看回方向导数的定义：

因此，最终我们得出了方向导数的计算公式：

我们知道，$cos\alpha ,cos\beta$表示的是某一个特定的方向，那么此时的偏导数也反应的是函数$f(x,y)$ 在这个方向上的变化率。不过我们知道，在 $M_0$ 点是有无数个方向的，这各种各样的方向对应都可以对应着一段曲线，而又恰好这些曲线的切线又是共面的，如下图所示：

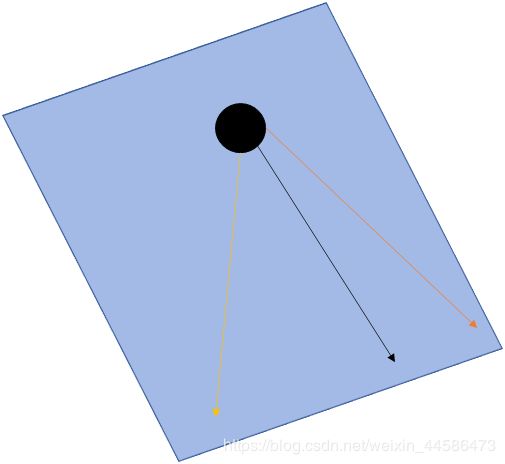
那些黑线就表示许多经过 M0 点的曲线的切线。他们都是在一个平面上的，那么这样就很清晰了：在这样一个平面上，总会是只有一个方向，使得函数的变化率是最大的。

如下图所示：如果这个黑球要滚下这个平面，那沿着黑线滚下的速度肯定是必沿着黄线或红线滚下的速度快。

我们再看会方向导数的公式：

它可以写成：

在这个表达式里面，$\overline{a_l}$ 是可以变化的，那么啥时候方向导数达到最大值呢？—— 就是 $\overline{a_l}$ 和 梯度同方向的时候！

因此，我们也可以说：$▽f$ 的方向就是函数下降最快的方向，因为当 $\overline{a_l}$ 和 梯度同方向的时候，方向导数的值等于 $|▽f|\cdot |\overline{a_l}|$，而 $|\overline{a_l}|=1$，所以方向导数的最大值就是梯度的模。

---

至此，这次的连载就要告一段路啦，我们今天引入了矢量微分算子，以及深入理解了方向导数和梯度的关系。那么在后面一个连载里面，我们就开始探寻 $Maxwell$ 方程的微分形式啦！